人教版八年级下册20.2.2极差和方差课件 (共24张PPT)
文档属性
| 名称 | 人教版八年级下册20.2.2极差和方差课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 08:16:08 | ||
图片预览





文档简介
(共24张PPT)
课程:数学
《极差和方差》
人教版
八年级下册 第3课时
第 20 章 数据的分析
教学目标
1.了解方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
知识与技能
经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,
积累统计经验。
过程与方法
培养学生的统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
14
24
19
16
20
10
22
23
25
23
21
20
新课导入
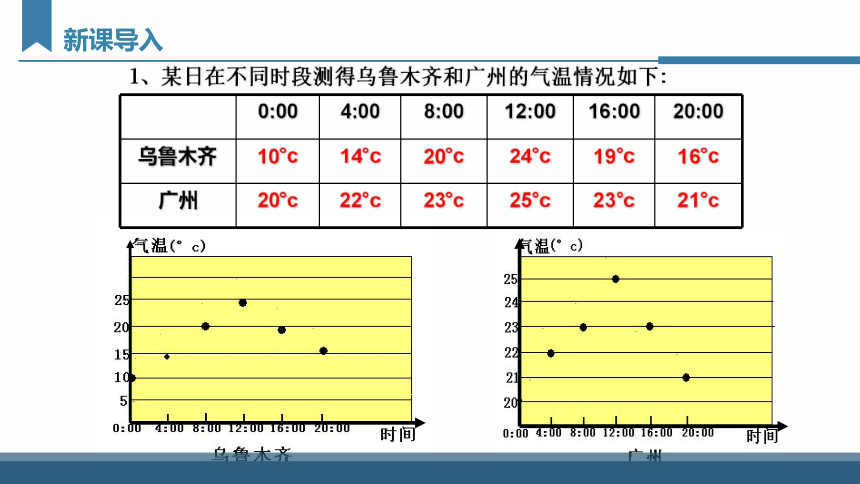
1、某日在不同时段测得乌鲁木齐和广州的气温情况如下:
0:00 4:00 8:00 12:00 16:00 20:00
乌鲁木齐 10°c 14°c 20°c 24°c 19°c 16°c
广州 20°c 22°c 23°c 25°c 23°c 21°c
探究新知
02
Explore new knowledge
22
23
25
23
21
20
探究新知
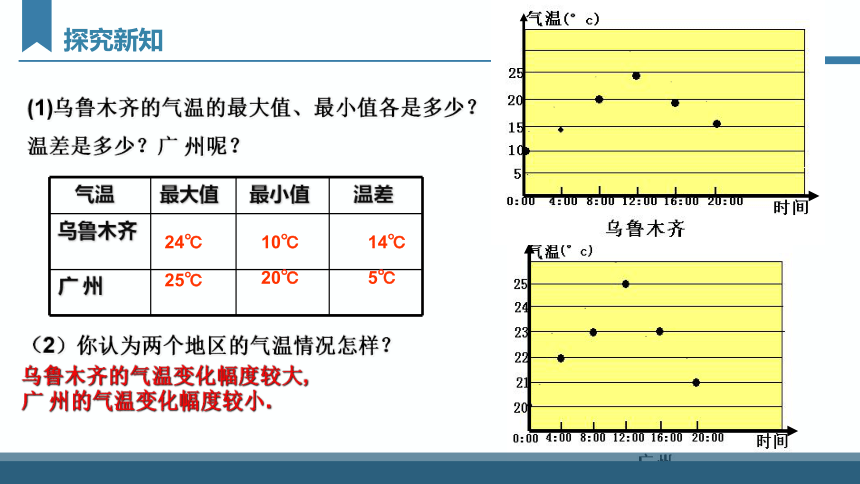
乌鲁木齐的气温变化幅度较大,
广 州的气温变化幅度较小.
(1)乌鲁木齐的气温的最大值、最小值各是多少?
温差是多少?广 州呢?
(2)你认为两个地区的气温情况怎样?
气温 最大值 最小值 温差
乌鲁木齐
广 州
24℃
10℃
14℃
25℃
20℃
5℃
14
24
19
16
20
10
探究新知
最大值-最小值.
一组数据中的最大数据与最小数据的差
极差:
极差=
作用:极差能够反映数据的变化范围.
极差是最简单的一种度量数据变化情况的量,但它受极端值的影响较大.
探究新知
实际问题
?
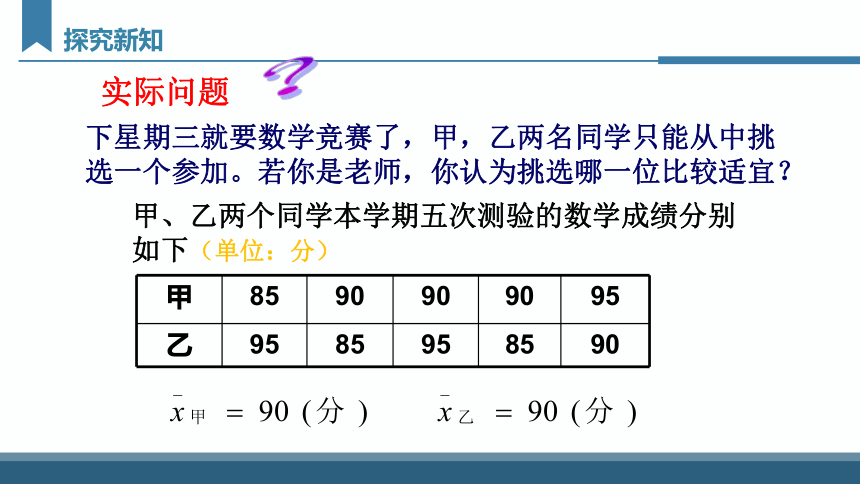
甲、乙两个同学本学期五次测验的数学成绩分别如下(单位:分)
下星期三就要数学竞赛了,甲,乙两名同学只能从中挑选一个参加。若你是老师,你认为挑选哪一位比较适宜?
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
80
85
90
95
100
成绩(分)
⑶ 现要挑选一名同学参加竞
赛,若你是老师,你认为挑
选哪一位比较适宜?为什么?
⑴ 请分别计算两名同学的平均成绩;
⑵ 请根据这两名同学的成绩在
下图中画出折线统计图;
0
1
2
3
4
5
甲,乙两名同学的测试成绩统计如下:
考试次数
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
谁的稳定性好?应以什么数据来衡量?
甲同学成绩与平均成绩的偏差的和:
乙同学成绩与平均成绩的偏差的和:
(85-90)+(90-90)+(90-90)+(90-90)+(95-90)=
0
(95-90)+(85-90)+(95-90)+(85-90)+(90-90)=
0
怎么办?
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
谁的稳定性好?应以什么数据来衡量?
甲同学成绩与平均成绩的偏差的平方和:
乙同学成绩与平均成绩的偏差的平方和:
找到啦!有区别了!
(85-90)2+(90-90)2+(90-90)2 +(90-90)2 +(95-90)2 =
50
(95-90)2+(85-90)2+(95-90)2 +(85-90)2 +(90-90)2 =
100
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
上述各偏差的平方和的大小还与什么有关?
——与考试次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性.
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2 、… (xn-x)2 ,那么我们用它们的平均数,即用
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
探究新知
方差越小,说明数据分布越集中,波动越小,越稳定.
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
定义
方差越大,说明数据分布越分散,波动越大,越不稳定.
探究新知
例1
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演
了舞剧《天鹅湖》,参加表演的女演员的身高
(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐
探究新知
解:甲、乙两团演员的平均身高分别是
课堂练习
03
class exercise
课堂练习
1、样本方差的作用是( )
(A ) 表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、 在样本方差的计算公式
数字10 表示 ,数字20表示 .
2、样本5、6、7、8、9的方差是 .
D
2
样本平均数
样本容量
课堂练习
4、计算下列各组数据的方差:
(1)6 6 6 6 6 6 6; 6 0
(2)5 5 6 6 6 7 7; 6 4/7
(3)3 3 4 6 8 9 9 ; 6 44/7
(4)3 3 3 6 9 9 9 ; 6 54/7
课堂练习
小明的烦恼
?
在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学 70 95 75 95 90
英语 80 85 90 85 85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学 110; ②英语 10
建议:英语较稳定但要提高; 数学不够稳定有待努力进步!
课堂小结
04
Class summary
课堂小结
谈谈自己这节课你学到了什么?
1.方差:各数据与平均数的差的平方的平均
数叫做这批数据的方差.
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
小结:
2.方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
在样本容量相同的情况下:
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定.
课堂小结
3.极差、方差的区别与联系
方差是用“先平均,再求差,然后平方,最后再平均”的方法得到的结果,主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数据的变化都将影响方差的结果,是一个对整组数据波动情况更敏感的指标。
区别:
极差是用一组数据中的最大值与最小值的差来反映数据的变化范围,主要反映一组数据中两个极端值之间的差异情况,对其他的数据的波动不敏感。
Thank you!
第 20 章 数据的分析
课程:数学
《极差和方差》
人教版
八年级下册 第3课时
第 20 章 数据的分析
教学目标
1.了解方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
知识与技能
经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,
积累统计经验。
过程与方法
培养学生的统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
14
24
19
16
20
10
22
23
25
23
21
20
新课导入
1、某日在不同时段测得乌鲁木齐和广州的气温情况如下:
0:00 4:00 8:00 12:00 16:00 20:00
乌鲁木齐 10°c 14°c 20°c 24°c 19°c 16°c
广州 20°c 22°c 23°c 25°c 23°c 21°c
探究新知
02
Explore new knowledge
22
23
25
23
21
20
探究新知
乌鲁木齐的气温变化幅度较大,
广 州的气温变化幅度较小.
(1)乌鲁木齐的气温的最大值、最小值各是多少?
温差是多少?广 州呢?
(2)你认为两个地区的气温情况怎样?
气温 最大值 最小值 温差
乌鲁木齐
广 州
24℃
10℃
14℃
25℃
20℃
5℃
14
24
19
16
20
10
探究新知
最大值-最小值.
一组数据中的最大数据与最小数据的差
极差:
极差=
作用:极差能够反映数据的变化范围.
极差是最简单的一种度量数据变化情况的量,但它受极端值的影响较大.
探究新知
实际问题
?
甲、乙两个同学本学期五次测验的数学成绩分别如下(单位:分)
下星期三就要数学竞赛了,甲,乙两名同学只能从中挑选一个参加。若你是老师,你认为挑选哪一位比较适宜?
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
80
85
90
95
100
成绩(分)
⑶ 现要挑选一名同学参加竞
赛,若你是老师,你认为挑
选哪一位比较适宜?为什么?
⑴ 请分别计算两名同学的平均成绩;
⑵ 请根据这两名同学的成绩在
下图中画出折线统计图;
0
1
2
3
4
5
甲,乙两名同学的测试成绩统计如下:
考试次数
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
谁的稳定性好?应以什么数据来衡量?
甲同学成绩与平均成绩的偏差的和:
乙同学成绩与平均成绩的偏差的和:
(85-90)+(90-90)+(90-90)+(90-90)+(95-90)=
0
(95-90)+(85-90)+(95-90)+(85-90)+(90-90)=
0
怎么办?
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
谁的稳定性好?应以什么数据来衡量?
甲同学成绩与平均成绩的偏差的平方和:
乙同学成绩与平均成绩的偏差的平方和:
找到啦!有区别了!
(85-90)2+(90-90)2+(90-90)2 +(90-90)2 +(95-90)2 =
50
(95-90)2+(85-90)2+(95-90)2 +(85-90)2 +(90-90)2 =
100
甲 85 90 90 90 95
乙 95 85 95 85 90
探究新知
上述各偏差的平方和的大小还与什么有关?
——与考试次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性.
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2 、… (xn-x)2 ,那么我们用它们的平均数,即用
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
探究新知
方差越小,说明数据分布越集中,波动越小,越稳定.
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
定义
方差越大,说明数据分布越分散,波动越大,越不稳定.
探究新知
例1
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演
了舞剧《天鹅湖》,参加表演的女演员的身高
(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐
探究新知
解:甲、乙两团演员的平均身高分别是
课堂练习
03
class exercise
课堂练习
1、样本方差的作用是( )
(A ) 表示总体的平均水平
(B)表示样本的平均水平
(C)准确表示总体的波动大小
(D)表示样本的波动大小
3、 在样本方差的计算公式
数字10 表示 ,数字20表示 .
2、样本5、6、7、8、9的方差是 .
D
2
样本平均数
样本容量
课堂练习
4、计算下列各组数据的方差:
(1)6 6 6 6 6 6 6; 6 0
(2)5 5 6 6 6 7 7; 6 4/7
(3)3 3 4 6 8 9 9 ; 6 44/7
(4)3 3 3 6 9 9 9 ; 6 54/7
课堂练习
小明的烦恼
?
在学校,小明本学期五次测验的数学成绩和英语成绩分别如下(单位:分)
数学 70 95 75 95 90
英语 80 85 90 85 85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学 110; ②英语 10
建议:英语较稳定但要提高; 数学不够稳定有待努力进步!
课堂小结
04
Class summary
课堂小结
谈谈自己这节课你学到了什么?
1.方差:各数据与平均数的差的平方的平均
数叫做这批数据的方差.
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
小结:
2.方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
在样本容量相同的情况下:
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定.
课堂小结
3.极差、方差的区别与联系
方差是用“先平均,再求差,然后平方,最后再平均”的方法得到的结果,主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数据的变化都将影响方差的结果,是一个对整组数据波动情况更敏感的指标。
区别:
极差是用一组数据中的最大值与最小值的差来反映数据的变化范围,主要反映一组数据中两个极端值之间的差异情况,对其他的数据的波动不敏感。
Thank you!
第 20 章 数据的分析
