1.2.3 矩形的性质与判定的综合应用—北师大版数学九年级上册课堂同步练(含答案)
文档属性
| 名称 | 1.2.3 矩形的性质与判定的综合应用—北师大版数学九年级上册课堂同步练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 464.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 12:57:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版数学九年级上册课堂同步练
第一章 特殊平行四边形
1.2 矩形的性质与判定
第3课时 矩形的性质与判定的综合应用
分类练
知识点 矩形的性质与判定的综合应用
1. 为了解居民的日常生活所需,某社区成立了服务站,如图是该社区辖区内的A,B,C三个小区位置示意图,其中AB=1 000 m,BC=600 m,AC=800 m.如果要求服务站到三个小区的距离相等,那么服务站设立的位置应在( )
A.AB的中点处 B.BC的中点处
C.AC的中点处 D.∠C的平分线与AB的交点处
2. 如图,在△ABC中,AC的中垂线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E.若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
A.2 B.2 C.3 D.3
3. 如图,E是矩形ABCD的边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为 .
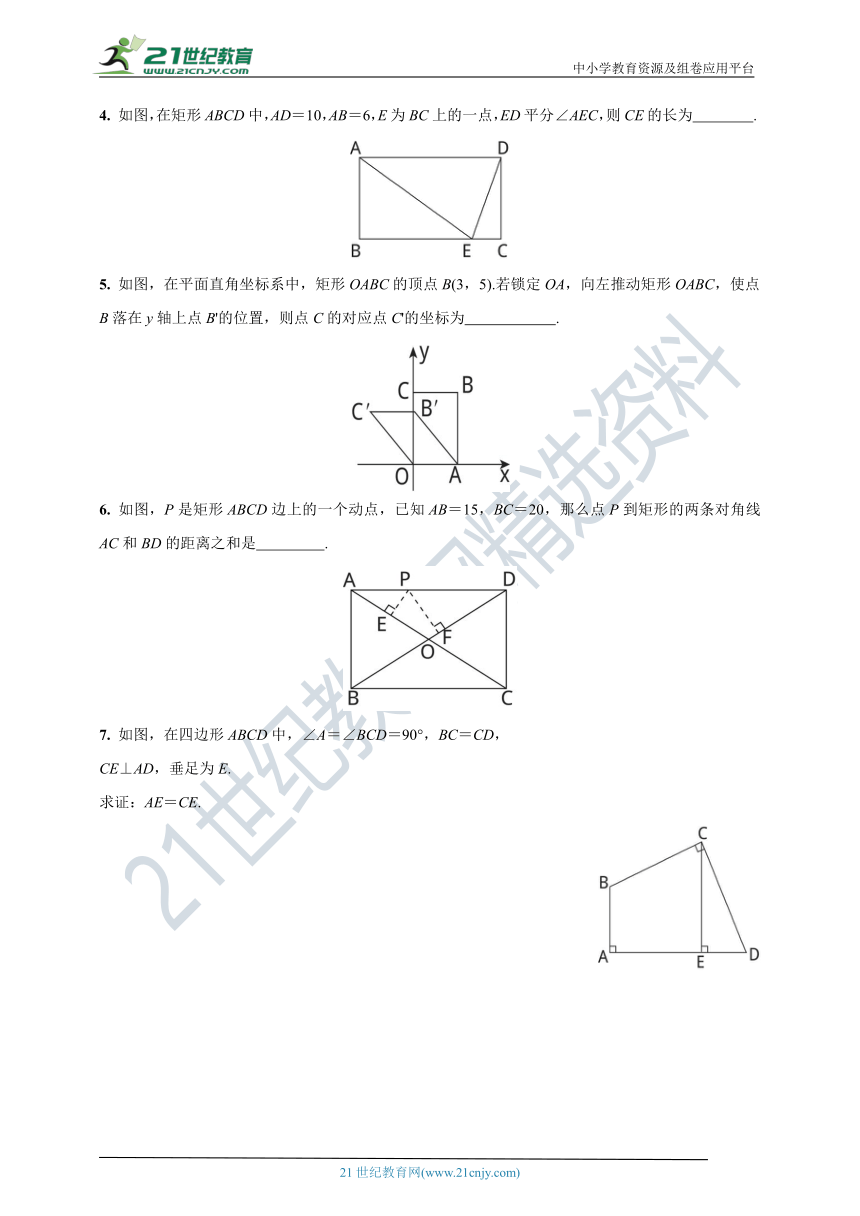
4. 如图,在矩形ABCD中,AD=10,AB=6,E为BC上的一点,ED平分∠AEC,则CE的长为 .
5. 如图,在平面直角坐标系中,矩形OABC的顶点B(3,5).若锁定OA,向左推动矩形OABC,使点B落在y轴上点B'的位置,则点C的对应点C'的坐标为 .
6. 如图,P是矩形ABCD边上的一个动点,已知AB=15,BC=20,那么点P到矩形的两条对角线AC和BD的距离之和是 .
7. 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD,
CE⊥AD,垂足为E.
求证:AE=CE.
提升练
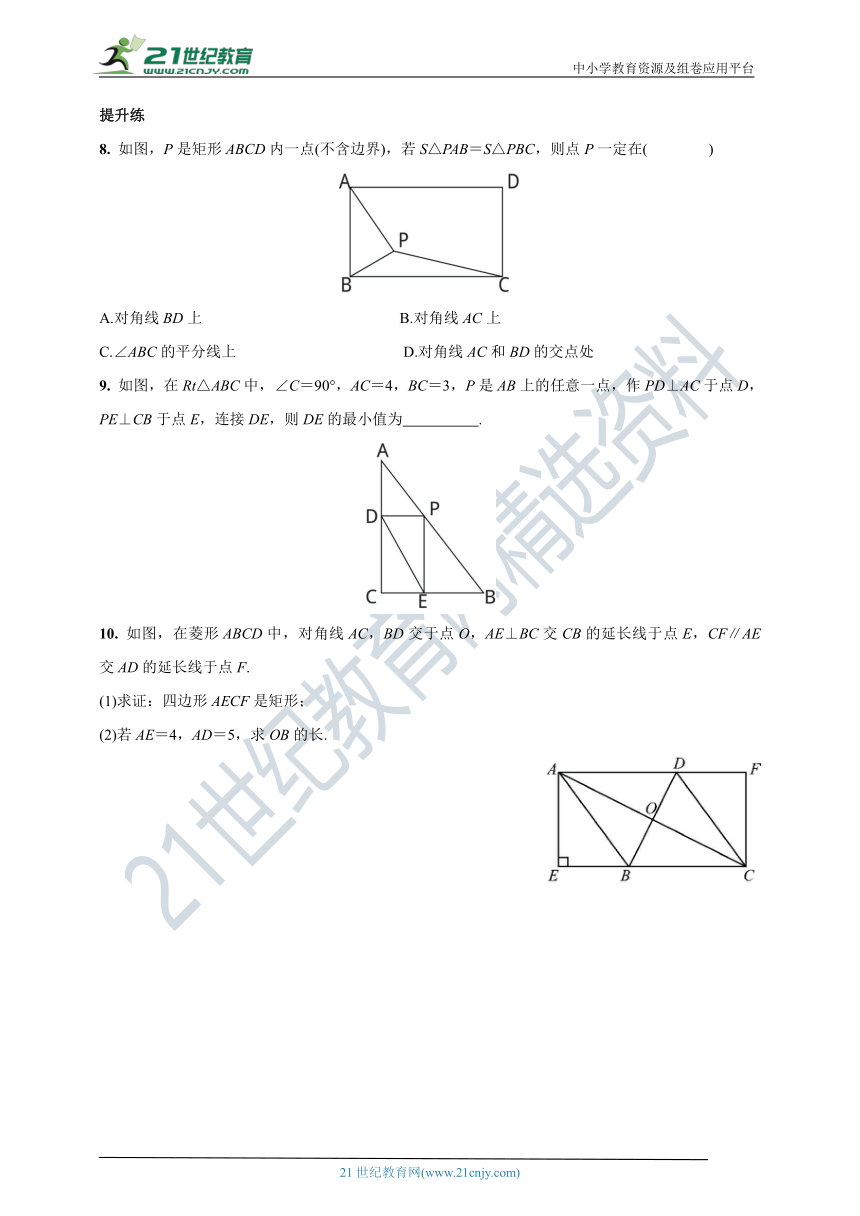
8. 如图,P是矩形ABCD内一点(不含边界),若S△PAB=S△PBC,则点P一定在( )
A.对角线BD上 B.对角线AC上
C.∠ABC的平分线上 D.对角线AC和BD的交点处
9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为 .
10. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB的延长线于点E,CF∥AE交AD的延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求OB的长.
拓展练
11. 如图,在△ABC中,O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)连接AE,AF.当点O在边AC上运动到什么位置时,四边形AECF是矩形 请说明理由.
参 考 答 案
1. C
2. 证明:∵BD是AC的垂直平分线,∴AD=DC,BD⊥CA,∴∠BDC=90°. 由题意知AB∥DE,AD∥BE,∴四边形ABED是平行四边形,∴AD=BE,∴DC=BE. 又∵DC∥BE,∴四边形BECD是平行四边形. ∵∠BDC=90°,∴平行四边形BECD是矩形.
3. A
4. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD. ∵CE=CD,∴AB=CE,∴四边形ABEC是平行四边形. ∵四边形ABCD是平行四边形,∴∠ABC=∠D. ∵∠AFC=2∠D,∴∠AFC=2∠ABC,∴∠ABF=∠BAF,∴FA=FB,∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形.
5. C
6. 20
7. 3
8. AC⊥BD
9. 证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAB+∠ABC=180°. ∵AE,BF分别平分∠DAB,∠ABC,∴∠BOK=∠OAB+∠OBA=(∠DAB+∠ABC)=90°,∴∠GOK=∠BOK=90°,同理可得∠OKH=90°,∠KHG=90°,∴四边形HGOK是矩形.
10. 解:(1)t (5-2t)(0≤t≤2.5)或(2t-5)(2.5<t≤5)
(2)∵四边形ABCD是矩形,∴AB=CD,AB∥CD,∴∠GAF=∠HCE. ∵G,H分别是AB,DC的中点,∴AG=CH. ∵AE=CF,∴AF=CE,∴△AFG≌△CEH(SAS),∴GF=HE,∠AFG=∠CEH,∴GF∥HE,∴四边形EGFH是平行四边形.
(3)连接GH.由(2)知四边形EGFH是平行四边形. ∵G,H分别是矩形ABCD的边AB,DC的中点,∴GH=BC=4 cm,∴当EF=GH=4 cm时,四边形EGFH是矩形. 分两种情况:①当0≤t≤2.5时,EF=(5-2t) cm,即5-2t=4,解得t=0.5;②当2.5<t≤5时,EF=(2t-5) cm,即2t-5=4,解得t=4.5. ∴当t=0.5或4.5时,四边形EGFH为矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版数学九年级上册课堂同步练
第一章 特殊平行四边形
1.2 矩形的性质与判定
第3课时 矩形的性质与判定的综合应用
分类练
知识点 矩形的性质与判定的综合应用
1. 为了解居民的日常生活所需,某社区成立了服务站,如图是该社区辖区内的A,B,C三个小区位置示意图,其中AB=1 000 m,BC=600 m,AC=800 m.如果要求服务站到三个小区的距离相等,那么服务站设立的位置应在( )
A.AB的中点处 B.BC的中点处
C.AC的中点处 D.∠C的平分线与AB的交点处
2. 如图,在△ABC中,AC的中垂线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E.若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
A.2 B.2 C.3 D.3
3. 如图,E是矩形ABCD的边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为 .
4. 如图,在矩形ABCD中,AD=10,AB=6,E为BC上的一点,ED平分∠AEC,则CE的长为 .
5. 如图,在平面直角坐标系中,矩形OABC的顶点B(3,5).若锁定OA,向左推动矩形OABC,使点B落在y轴上点B'的位置,则点C的对应点C'的坐标为 .
6. 如图,P是矩形ABCD边上的一个动点,已知AB=15,BC=20,那么点P到矩形的两条对角线AC和BD的距离之和是 .
7. 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD,
CE⊥AD,垂足为E.
求证:AE=CE.
提升练
8. 如图,P是矩形ABCD内一点(不含边界),若S△PAB=S△PBC,则点P一定在( )
A.对角线BD上 B.对角线AC上
C.∠ABC的平分线上 D.对角线AC和BD的交点处
9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为 .
10. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB的延长线于点E,CF∥AE交AD的延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求OB的长.
拓展练
11. 如图,在△ABC中,O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)连接AE,AF.当点O在边AC上运动到什么位置时,四边形AECF是矩形 请说明理由.
参 考 答 案
1. C
2. 证明:∵BD是AC的垂直平分线,∴AD=DC,BD⊥CA,∴∠BDC=90°. 由题意知AB∥DE,AD∥BE,∴四边形ABED是平行四边形,∴AD=BE,∴DC=BE. 又∵DC∥BE,∴四边形BECD是平行四边形. ∵∠BDC=90°,∴平行四边形BECD是矩形.
3. A
4. 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD. ∵CE=CD,∴AB=CE,∴四边形ABEC是平行四边形. ∵四边形ABCD是平行四边形,∴∠ABC=∠D. ∵∠AFC=2∠D,∴∠AFC=2∠ABC,∴∠ABF=∠BAF,∴FA=FB,∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形.
5. C
6. 20
7. 3
8. AC⊥BD
9. 证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAB+∠ABC=180°. ∵AE,BF分别平分∠DAB,∠ABC,∴∠BOK=∠OAB+∠OBA=(∠DAB+∠ABC)=90°,∴∠GOK=∠BOK=90°,同理可得∠OKH=90°,∠KHG=90°,∴四边形HGOK是矩形.
10. 解:(1)t (5-2t)(0≤t≤2.5)或(2t-5)(2.5<t≤5)
(2)∵四边形ABCD是矩形,∴AB=CD,AB∥CD,∴∠GAF=∠HCE. ∵G,H分别是AB,DC的中点,∴AG=CH. ∵AE=CF,∴AF=CE,∴△AFG≌△CEH(SAS),∴GF=HE,∠AFG=∠CEH,∴GF∥HE,∴四边形EGFH是平行四边形.
(3)连接GH.由(2)知四边形EGFH是平行四边形. ∵G,H分别是矩形ABCD的边AB,DC的中点,∴GH=BC=4 cm,∴当EF=GH=4 cm时,四边形EGFH是矩形. 分两种情况:①当0≤t≤2.5时,EF=(5-2t) cm,即5-2t=4,解得t=0.5;②当2.5<t≤5时,EF=(2t-5) cm,即2t-5=4,解得t=4.5. ∴当t=0.5或4.5时,四边形EGFH为矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
