北师大版 数学六年级下册 第四单元测试卷(含答案)
文档属性
| 名称 | 北师大版 数学六年级下册 第四单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 22:38:01 | ||
图片预览



文档简介
北师大版六年级下册第四单元测试卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
一、填空题(共46分)
1.(本题3分)《童话书》的单价一定,购买的本数与总价成(________)比例。
2.(本题6分)如果y=5x,那么x和y成________比例;如果xy=5,那么x和y成________比例。
3.(本题9分)路程一定,汽车行驶的时间和速度成(________)比例;单价一定,牛奶的数量和总价成(________)比例;一袋大米,剩下的和吃掉的(________)比例。
4.(本题8分)下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?
(1)宽不变,长方形的面积与长。(______)
(2)运一堆煤,车的载质量和需要运的次数。(______)
(3)有10个苹果,已吃的个数与未吃的个数。(______)
(4)打一份稿件的字数一定,打字所用的时间和打字速度。(______)
5.(本题8分)工地要运一批水泥,每天运的吨数和运的天数如下表。
每天运的吨数/吨 60 30 20 15 10
运的天数/天 1 2 3 4 6
(1)表中相关联的两种量是(________)和(________)
(2)每天运的吨数增加,运的天数就会(________);每天运的吨数减少,运的天数就会(________)。
(3)表中表示的几种量的关系是(________)一定,(________)与(________)成(________)比例
6.(本题6分)下图描述了一个游泳池进水管打开后的进水情况。
①这个游泳池的进水量与时间成(______)比例。
②照这样的速度,要注水800立方米,需要(______)分钟。
7.(本题3分)甲数和乙数互为倒数,那么甲、乙两数成(________)比例关系。
8.(本题3分)把一根木料锯成4段要用12分钟,照这样,如果锯成8段,一共需要(________)分钟。
二、判断题(共10分)
9.(本题2分)甲数和乙数互为倒数,那么甲数和乙数成反比例. (____)
10.(本题2分)两种相关联的量,不成正比例就成反比例。(______)
11.(本题2分)车轮周长一定,车轮行驶的路程和转数成正比例关系。(________)
12.(本题2分)每袋花生的质量一定,花生的总质量和袋数成正比例。(________)
13.(本题2分)出盐率一定,盐的质量和海水质量成正比例. (______)
三、选择题(共10分)
14.(本题2分)下列比例中的两种量成正比例关系的是( )。
A.总价一定,单价和数量 B.圆的周长和半径 C.小明的身高和年龄 D.平行四边形的面积一定,底和高
15.(本题2分)下列等式中,x与y(x、y均不为0)成反比例关系的是( )。
A. B. C.
16.(本题2分)下列哪个图像是正比例图像( )。
A. B. C.D.
17.(本题2分)表示和成正比例关系的式子是( )。
A.(一定) B.(一定) C.(一定)
18.(本题2分)三角形的面积一定,它的底和高( )。
A.成正比例 B.成反比例 C.不成比例 D.也是一定的
四、解答题(共34分)
19.(本题8分)用a,h分别表示面积为96平方厘米的平行四边形的底和高,请完成下表,并回答问题。
1 2 3 4 6 8 12 24 48
96
(1)h随着a的增加是怎样变化的?
(2)h与a成什么关系?为什么?
(3)当平行四边形的底为15厘米时,高是多少厘米?
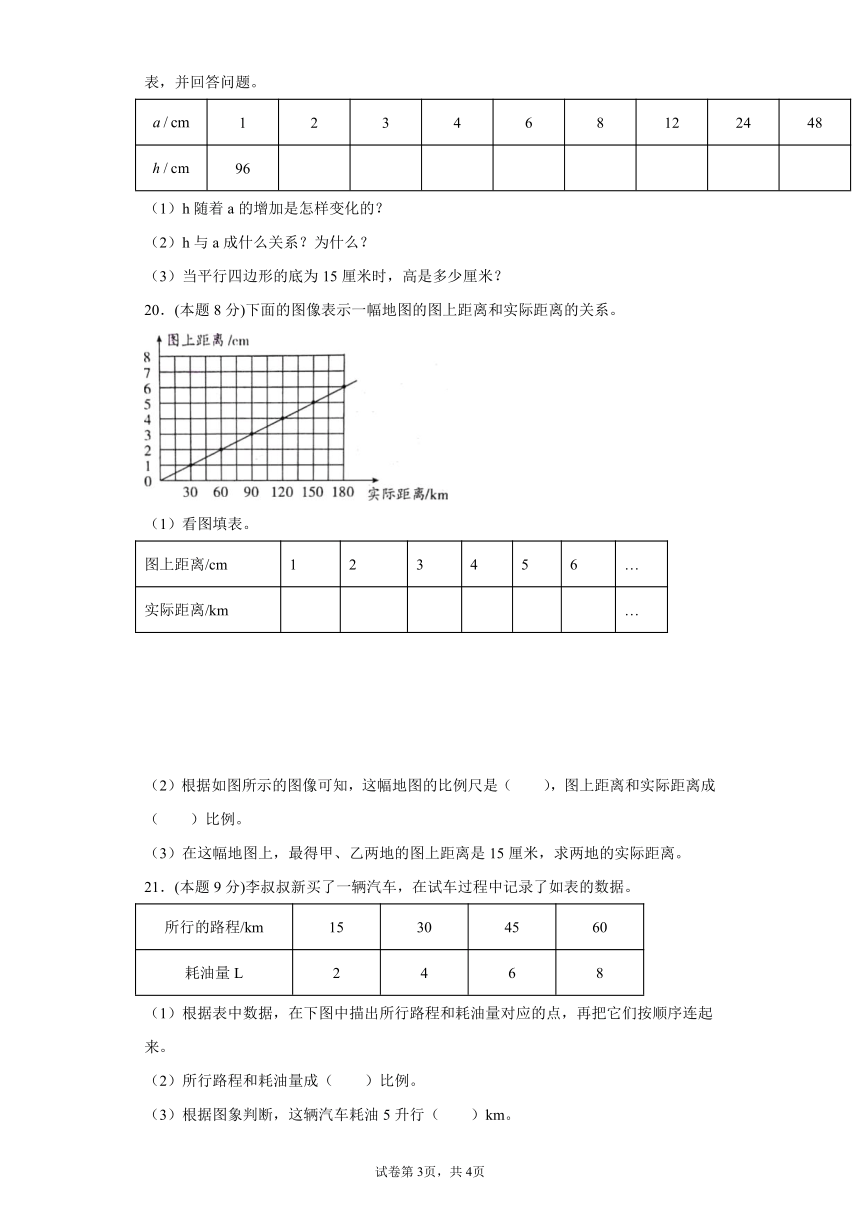
20.(本题8分)下面的图像表示一幅地图的图上距离和实际距离的关系。
(1)看图填表。
图上距离/cm 1 2 3 4 5 6 …
实际距离/km …
(2)根据如图所示的图像可知,这幅地图的比例尺是( ),图上距离和实际距离成( )比例。
(3)在这幅地图上,最得甲、乙两地的图上距离是15厘米,求两地的实际距离。
21.(本题9分)李叔叔新买了一辆汽车,在试车过程中记录了如表的数据。
所行的路程/km 15 30 45 60
耗油量L 2 4 6 8
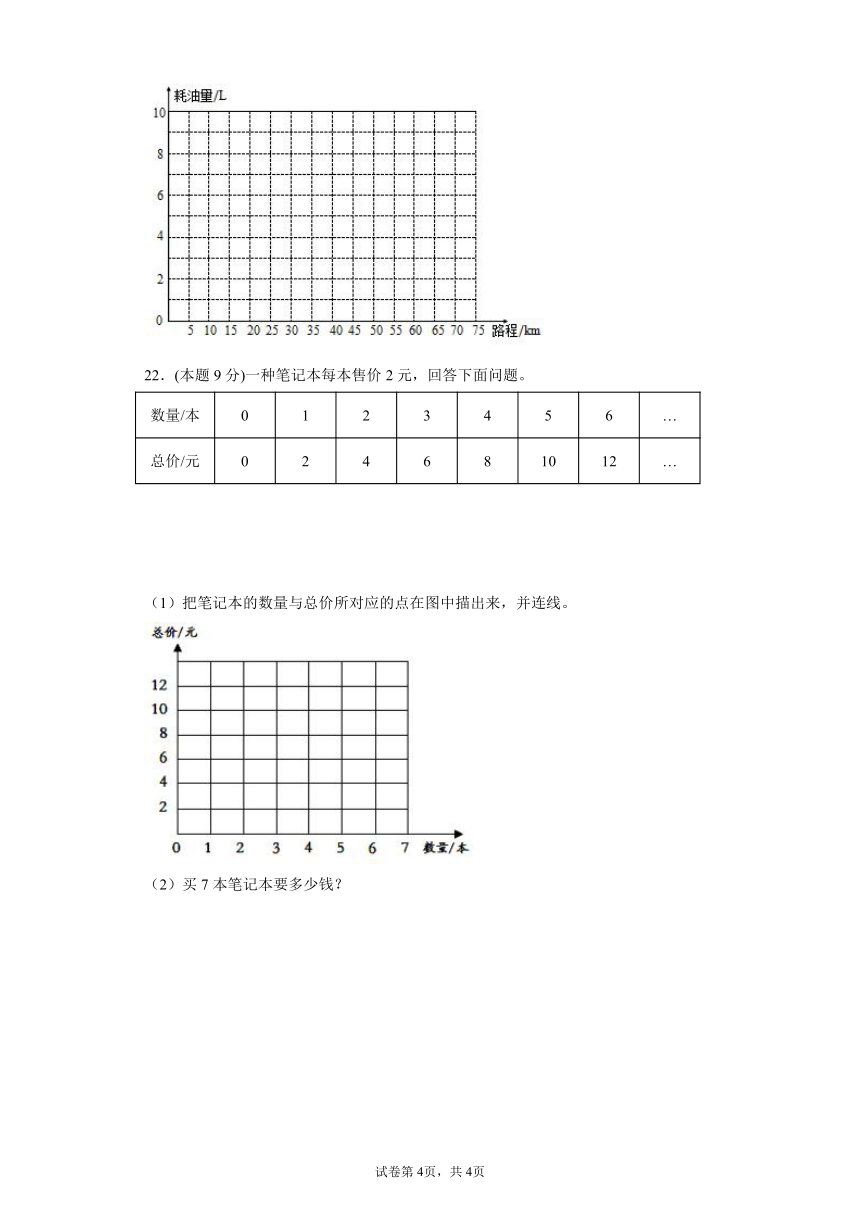
(1)根据表中数据,在下图中描出所行路程和耗油量对应的点,再把它们按顺序连起来。
(2)所行路程和耗油量成( )比例。
(3)根据图象判断,这辆汽车耗油5升行( )km。
22.(本题9分)一种笔记本每本售价2元,回答下面问题。
数量/本 0 1 2 3 4 5 6 …
总价/元 0 2 4 6 8 10 12 …
(1)把笔记本的数量与总价所对应的点在图中描出来,并连线。
(2)买7本笔记本要多少钱?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.正
【分析】
根据本数,总价,单价之间的关系;总价÷本数=单价(一定)。即=单价(一定),由此即可判断。
【详解】
通过分析可知,总价与本数的比值一定,即本数与总价成正比例。
【点睛】
本题主要考查正比例的判断,两个相关联的量的比值一定,即这两个相关联的量成正比例关系。
2.正 反
【分析】
正比例:两种相关联的量,一种量变化,另一种量也随着相同变化,如果两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做正比例的量,它们的关系叫做正比例的关系。反比例:两种相关联的量,一种量变化,另一种量也随着相反变化,如果两种量相对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例的关系。
【详解】
根据分析可知,如果,即,所以x和y成正比例;如果,那么x和y成反比例。
【点睛】
此题主要考查学生对正、反比例关系判定方法的应用。
3.反 正 不成
【分析】
两个相关联的量,如果它们对应的比值一定,则成正比例关系;如果它们对应的乘积一定,则成反比例关系,否则不成比例,据此解答。
【详解】
时间×速度=路程(一定),所以路程一定,汽车行驶的时间和速度成反比例;
总价÷数量=单价(一定),所以单价一定,牛奶的数量和总价成正比例;
剩下的+吃掉的=大米总量(一定),和一定,所以一袋大米,剩下的和吃掉的不成比例。
【点睛】
此题考查了正反比例的辨别,主要看两个量的比值一定,还是乘积一定,再进一步判断。
4.正比例 反比例 不成比例 反比例
【分析】
两种相关联的量,商一定,则成正比例;积一定,则成反比例。
【详解】
(1)长方形的面积÷长=宽(一定)
宽一定,即长方形的面积和长的商一定,则长方形的面积与长成正比例。
(2)车载质量×需要运的次数=这堆煤的总质量(一定)
这堆煤的总质量一定,即车载质量和需要运的次数的积一定,则车载质量和需要运的次数成反比例。
(3)已吃的个数+未吃的个数=10(一定),和一定,不符合正比例和反比例的意义,则已吃的个数与未吃的个数不成比例。
(4)打字所用的时间×打字速度=稿件的字数(一定)
稿件的字数一定,即打字所用的时间和打字速度的积一定,则打字所用的时间和打字速度成反比例。
【点睛】
本题考查正比例和反比例关系的辨认,要判断两种量是正比例还是反比例,要看它们的商或积是否一定。
5.每天运的吨数 运的天数 减少 增加 水泥的总量 每天运的吨数 运的天数 反
【分析】
(1)由表可得相关的两个量是每天运的吨数和运的天数。
(2)根据题目可得水泥的总吨数是一定的60吨,所以每天运的吨数增加,运的天数就会减少;每天运的吨数减少,运的天数就会增加。
(3)根据表格可得:每天运的吨数×运的天数=总吨数(一定),所以每天运的吨数和运的天数成反比例关系。
【详解】
(1)表中相关联的两种量是每天运的吨数和运的天数。
(2)每天运的吨数增加,运的天数就会减少;每天运的吨数减少,运的天数就会增加。
(3)表中表示的几种量的关系是水泥的总量一定,每天运的吨数与运的天数成反比例。
【点睛】
本题考查反比例的应用,把表格中的数据进行分析,观察两个量的积和商是否一定,再判断比例关系。
6.正 80
【分析】
①根据图像特点填空即可;
②1分钟进水10立方米,用注水量÷每分钟进水量即可。
【详解】
①这是正比例图像,所以这个游泳池的进水量与时间成( 正 )比例。
②800÷10=80(分钟),所以要注水800立方米,需要( 80 )分钟。
【点睛】
本题考查了正比例,正比例图像是一条经过原点的直线。
7.反
【分析】
判断甲和乙是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。据此进行判断。
【详解】
如果甲和乙互为倒数,则有甲×乙=1(一定)
甲和乙对应的乘积一定,那么甲和乙一定成反比例关系
甲、乙两数成反比例关系
【点睛】
此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出判断;也考查了倒数的意义:乘积是1的两个数互为倒数。
8.28
【分析】
由题意可知:一根木料锯成4段,需要锯(4-1)次,锯成8段需要锯(8-1)次,锯每次需要的时间一定,则时间与锯的次数成正比,据此即可列比例求解。
【详解】
12÷(4-1)×(8-1)
=12÷3×7
=4×7
=28(分钟)
【点睛】
本题主要考查植树问题,明确锯每次需要的时间一定,则时间与锯的次数成正比是解题的关键。
9.正确
【分析】
考察了学生认识和辨别正比例和反比例的能力
【详解】
甲数和乙数互为倒数,说明甲数和乙数的乘积是1,所以甲数和乙数成反比例
10.×
【分析】
相关联的两个量,如果它们的比值一定,那么他们成正比例;如果它们的积一定,那么它们成反比例。例如两个量的和一定或者差一定等,它们是不成比例的。
【详解】
两种相关联的量,要么成正比例或者成反比例,也可能不成比例。
故答案为:×
【点睛】
本题考查相关联的两个量之间的比例关系,注意相关联的两个量,只有积一定或者比值一定时,才会成比例关系。
11.√
【分析】
根据x÷y=k(一定),x和y成正比例关系,进行辨识即可。
【详解】
车轮行驶的路程÷转数=车轮周长(一定),车轮行驶的路程和转数成正比例关系,所以原题说法正确。
【点睛】
关键是理解正比例的意义,商一定是正比例关系。
12.√
【分析】
根据题意可知 “=每袋花生的质量(一定)”,比值一定,所以花生的总质量和袋数成正比例关系,据此解答即可。
【详解】
每袋花生的质量一定,花生的总质量和袋数成正比例,原题说法正确;
故答案为:√。
【点睛】
解答本题的关键是要明确成正比例关系的两个量比值一定。
13.√
【详解】
略
14.B
【分析】
判断两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;据此逐项分析后再选择。
【详解】
A.单价×数量=总价(一定),是积一定,所以单价和数量不成正比例;
B.因为圆的周长=圆周率×半径×2,周长÷半径=圆周率(一定)×2,所以圆的周长和半径成正比例;
C.小明的身高和年龄对应的比值或乘积都不一定,所以小明的身高和年龄不成比例;
D.平行四边形的面积=底×高,底和高的积一定,所以不成正比例。
故答案为:B。
【点睛】
此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
15.B
【分析】
根据xy=k(一定),x和y成反比例关系,进行选择。
【详解】
A.和的关系,不成比例关系;
B.乘积一定,成反比例关系;
C.比值一定,成正比例关系。
故答案为:B
【点睛】
关键是理解反比例的意义,积一定是反比例关系。
16.B
【分析】
两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的比值一定,即 =k(定值),那么这两个量叫做成正比例的量,它们的关系叫做正比例关系,由此判断即可;
【详解】
A.一个量变化,另一个量不变,不是正比例;
B. 一个量增加,另一个量也随着增加,成正比例;
C.一个量增加,另一个量随着减小,不成比例;
D. 一个量变化,另一个量不变,不是正比例;
故答案为:B
【点睛】
本题考查正比例图像的认识,需要熟练掌握正比例关系的特点,解答时注意,成正比例关系的图像就是一条经过原点的直线。
17.C
【分析】
根据(一定),x和y成正比例关系,进行选择。
【详解】
A. (一定),x和y不成比例关系;
B. (一定),x和y成反比例关系;
C. (一定),x和y成正比例关系。
故答案为:C
【点睛】
本题考查了辨识正比例的量,商一定是正比例关系,积一定是反比例关系。
18.B
【分析】
三角形的面积=底×高÷2,三角形的面积一定,说明底与高的乘积一定,根据反比例的意义可知,三角形的面积一定,它的底和高成反比例。
【详解】
根据分析可得,三角形的面积一定,它的底和高成反比例。
故答案为:B。
【点睛】
本题考查反比例的意义、三角形的面积,解答本题的关键是掌握反比例的意义。
19.
1 2 3 4 6 8 12 24 48
96 48 32 24 16 12 8 4 2
(1)h随着a的增加而减少;
(2)因为底×高=平行四边形的面积(一定),所以平行四边形底和高成反比例;
(3)6.4厘米
【分析】
(1)用面积÷底即可求出对应的高,,由此解答;
(2)平行四边形的面积=底×高,面积一定也是就是底和高乘反比例关系;据此解答;
(3)设高为x厘米,根据平行四边形的面积=底×高列出方程求解即可。
【详解】
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
填表如下:
1 2 3 4 6 8 12 24 48
96 48 32 24 16 12 8 4 2
(1)h随着a的增加而减少。
(2)因为底×高=平行四边形的面积(一定),所以平行四边形底和高成反比例。
(3)设高为厘米,
答:高是6.4厘米。
【点睛】
本题主要考查反比例关系的实际应用。
20.(1)
图上距离/cm 1 2 3 4 5 6 …
实际距离/km 30 60 90 120 150 180 …
(2)1∶3000000;正。
(3)450km。
【分析】
(1)看图可知:横轴为实际距离,纵轴为图上距离,再根据表中的数据一一对应在图中即可找出数值;(2)通过图上距离∶实际距离=比例尺即可求出;(3)通过图上距离÷比例尺=实际距离,代入数据即可求解。
【详解】
(1)看图填表。
图上距离/cm 1 2 3 4 5 6 …
实际距离/km 30 60 90 120 150 180 …
(2)30km=3000000cm,所以比例尺=1∶3000000。
故根据如图所示的图像可知,这幅地图的比例尺是(1∶3000000),图上距离和实际距离的比值一定,成( 正 )比例。
(3)实际距离:15÷=15×3000000=45000000(cm),45000000cm=45000000÷100000=450km。 故两地的实际距离为450km。
【点睛】
此题主要考查比例尺的应用以及提取图中信息的能力。
21.(1)见详解;(2)正;(3)37.5
【分析】
(1)根据统计表中的数据完成统计图。
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;由此解答即可。
(3)根据图象,观察纵轴5L所对应的横轴的数据,即可得出结论。
【详解】
(1)画图如下:
(2)15÷2=30÷4=45÷6=60÷8=7.5(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例。
(3)观察图表,这辆汽车耗油5升行37.5km。
【点评】
此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
22.(1)如图所示:
(2)14元
【分析】
根据数据描点连线;根据单价一定,求买7本书要多少钱。
【详解】
(1)根据数据描点连线,如图所示:
(2)单价=总价÷数量,笔记本的单价是一定的,所以7本笔记本需要:7×2=14元。
故答案为:(1)如图所示:
(2)14元。
【点睛】
本题考查反比例的意义,描点连线时是根据数量和总价所对应的的数描点,再把点按顺序连接起来。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
一、填空题(共46分)
1.(本题3分)《童话书》的单价一定,购买的本数与总价成(________)比例。
2.(本题6分)如果y=5x,那么x和y成________比例;如果xy=5,那么x和y成________比例。
3.(本题9分)路程一定,汽车行驶的时间和速度成(________)比例;单价一定,牛奶的数量和总价成(________)比例;一袋大米,剩下的和吃掉的(________)比例。
4.(本题8分)下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?
(1)宽不变,长方形的面积与长。(______)
(2)运一堆煤,车的载质量和需要运的次数。(______)
(3)有10个苹果,已吃的个数与未吃的个数。(______)
(4)打一份稿件的字数一定,打字所用的时间和打字速度。(______)
5.(本题8分)工地要运一批水泥,每天运的吨数和运的天数如下表。
每天运的吨数/吨 60 30 20 15 10
运的天数/天 1 2 3 4 6
(1)表中相关联的两种量是(________)和(________)
(2)每天运的吨数增加,运的天数就会(________);每天运的吨数减少,运的天数就会(________)。
(3)表中表示的几种量的关系是(________)一定,(________)与(________)成(________)比例
6.(本题6分)下图描述了一个游泳池进水管打开后的进水情况。
①这个游泳池的进水量与时间成(______)比例。
②照这样的速度,要注水800立方米,需要(______)分钟。
7.(本题3分)甲数和乙数互为倒数,那么甲、乙两数成(________)比例关系。
8.(本题3分)把一根木料锯成4段要用12分钟,照这样,如果锯成8段,一共需要(________)分钟。
二、判断题(共10分)
9.(本题2分)甲数和乙数互为倒数,那么甲数和乙数成反比例. (____)
10.(本题2分)两种相关联的量,不成正比例就成反比例。(______)
11.(本题2分)车轮周长一定,车轮行驶的路程和转数成正比例关系。(________)
12.(本题2分)每袋花生的质量一定,花生的总质量和袋数成正比例。(________)
13.(本题2分)出盐率一定,盐的质量和海水质量成正比例. (______)
三、选择题(共10分)
14.(本题2分)下列比例中的两种量成正比例关系的是( )。
A.总价一定,单价和数量 B.圆的周长和半径 C.小明的身高和年龄 D.平行四边形的面积一定,底和高
15.(本题2分)下列等式中,x与y(x、y均不为0)成反比例关系的是( )。
A. B. C.
16.(本题2分)下列哪个图像是正比例图像( )。
A. B. C.D.
17.(本题2分)表示和成正比例关系的式子是( )。
A.(一定) B.(一定) C.(一定)
18.(本题2分)三角形的面积一定,它的底和高( )。
A.成正比例 B.成反比例 C.不成比例 D.也是一定的
四、解答题(共34分)
19.(本题8分)用a,h分别表示面积为96平方厘米的平行四边形的底和高,请完成下表,并回答问题。
1 2 3 4 6 8 12 24 48
96
(1)h随着a的增加是怎样变化的?
(2)h与a成什么关系?为什么?
(3)当平行四边形的底为15厘米时,高是多少厘米?
20.(本题8分)下面的图像表示一幅地图的图上距离和实际距离的关系。
(1)看图填表。
图上距离/cm 1 2 3 4 5 6 …
实际距离/km …
(2)根据如图所示的图像可知,这幅地图的比例尺是( ),图上距离和实际距离成( )比例。
(3)在这幅地图上,最得甲、乙两地的图上距离是15厘米,求两地的实际距离。
21.(本题9分)李叔叔新买了一辆汽车,在试车过程中记录了如表的数据。
所行的路程/km 15 30 45 60
耗油量L 2 4 6 8
(1)根据表中数据,在下图中描出所行路程和耗油量对应的点,再把它们按顺序连起来。
(2)所行路程和耗油量成( )比例。
(3)根据图象判断,这辆汽车耗油5升行( )km。
22.(本题9分)一种笔记本每本售价2元,回答下面问题。
数量/本 0 1 2 3 4 5 6 …
总价/元 0 2 4 6 8 10 12 …
(1)把笔记本的数量与总价所对应的点在图中描出来,并连线。
(2)买7本笔记本要多少钱?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.正
【分析】
根据本数,总价,单价之间的关系;总价÷本数=单价(一定)。即=单价(一定),由此即可判断。
【详解】
通过分析可知,总价与本数的比值一定,即本数与总价成正比例。
【点睛】
本题主要考查正比例的判断,两个相关联的量的比值一定,即这两个相关联的量成正比例关系。
2.正 反
【分析】
正比例:两种相关联的量,一种量变化,另一种量也随着相同变化,如果两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做正比例的量,它们的关系叫做正比例的关系。反比例:两种相关联的量,一种量变化,另一种量也随着相反变化,如果两种量相对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例的关系。
【详解】
根据分析可知,如果,即,所以x和y成正比例;如果,那么x和y成反比例。
【点睛】
此题主要考查学生对正、反比例关系判定方法的应用。
3.反 正 不成
【分析】
两个相关联的量,如果它们对应的比值一定,则成正比例关系;如果它们对应的乘积一定,则成反比例关系,否则不成比例,据此解答。
【详解】
时间×速度=路程(一定),所以路程一定,汽车行驶的时间和速度成反比例;
总价÷数量=单价(一定),所以单价一定,牛奶的数量和总价成正比例;
剩下的+吃掉的=大米总量(一定),和一定,所以一袋大米,剩下的和吃掉的不成比例。
【点睛】
此题考查了正反比例的辨别,主要看两个量的比值一定,还是乘积一定,再进一步判断。
4.正比例 反比例 不成比例 反比例
【分析】
两种相关联的量,商一定,则成正比例;积一定,则成反比例。
【详解】
(1)长方形的面积÷长=宽(一定)
宽一定,即长方形的面积和长的商一定,则长方形的面积与长成正比例。
(2)车载质量×需要运的次数=这堆煤的总质量(一定)
这堆煤的总质量一定,即车载质量和需要运的次数的积一定,则车载质量和需要运的次数成反比例。
(3)已吃的个数+未吃的个数=10(一定),和一定,不符合正比例和反比例的意义,则已吃的个数与未吃的个数不成比例。
(4)打字所用的时间×打字速度=稿件的字数(一定)
稿件的字数一定,即打字所用的时间和打字速度的积一定,则打字所用的时间和打字速度成反比例。
【点睛】
本题考查正比例和反比例关系的辨认,要判断两种量是正比例还是反比例,要看它们的商或积是否一定。
5.每天运的吨数 运的天数 减少 增加 水泥的总量 每天运的吨数 运的天数 反
【分析】
(1)由表可得相关的两个量是每天运的吨数和运的天数。
(2)根据题目可得水泥的总吨数是一定的60吨,所以每天运的吨数增加,运的天数就会减少;每天运的吨数减少,运的天数就会增加。
(3)根据表格可得:每天运的吨数×运的天数=总吨数(一定),所以每天运的吨数和运的天数成反比例关系。
【详解】
(1)表中相关联的两种量是每天运的吨数和运的天数。
(2)每天运的吨数增加,运的天数就会减少;每天运的吨数减少,运的天数就会增加。
(3)表中表示的几种量的关系是水泥的总量一定,每天运的吨数与运的天数成反比例。
【点睛】
本题考查反比例的应用,把表格中的数据进行分析,观察两个量的积和商是否一定,再判断比例关系。
6.正 80
【分析】
①根据图像特点填空即可;
②1分钟进水10立方米,用注水量÷每分钟进水量即可。
【详解】
①这是正比例图像,所以这个游泳池的进水量与时间成( 正 )比例。
②800÷10=80(分钟),所以要注水800立方米,需要( 80 )分钟。
【点睛】
本题考查了正比例,正比例图像是一条经过原点的直线。
7.反
【分析】
判断甲和乙是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。据此进行判断。
【详解】
如果甲和乙互为倒数,则有甲×乙=1(一定)
甲和乙对应的乘积一定,那么甲和乙一定成反比例关系
甲、乙两数成反比例关系
【点睛】
此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出判断;也考查了倒数的意义:乘积是1的两个数互为倒数。
8.28
【分析】
由题意可知:一根木料锯成4段,需要锯(4-1)次,锯成8段需要锯(8-1)次,锯每次需要的时间一定,则时间与锯的次数成正比,据此即可列比例求解。
【详解】
12÷(4-1)×(8-1)
=12÷3×7
=4×7
=28(分钟)
【点睛】
本题主要考查植树问题,明确锯每次需要的时间一定,则时间与锯的次数成正比是解题的关键。
9.正确
【分析】
考察了学生认识和辨别正比例和反比例的能力
【详解】
甲数和乙数互为倒数,说明甲数和乙数的乘积是1,所以甲数和乙数成反比例
10.×
【分析】
相关联的两个量,如果它们的比值一定,那么他们成正比例;如果它们的积一定,那么它们成反比例。例如两个量的和一定或者差一定等,它们是不成比例的。
【详解】
两种相关联的量,要么成正比例或者成反比例,也可能不成比例。
故答案为:×
【点睛】
本题考查相关联的两个量之间的比例关系,注意相关联的两个量,只有积一定或者比值一定时,才会成比例关系。
11.√
【分析】
根据x÷y=k(一定),x和y成正比例关系,进行辨识即可。
【详解】
车轮行驶的路程÷转数=车轮周长(一定),车轮行驶的路程和转数成正比例关系,所以原题说法正确。
【点睛】
关键是理解正比例的意义,商一定是正比例关系。
12.√
【分析】
根据题意可知 “=每袋花生的质量(一定)”,比值一定,所以花生的总质量和袋数成正比例关系,据此解答即可。
【详解】
每袋花生的质量一定,花生的总质量和袋数成正比例,原题说法正确;
故答案为:√。
【点睛】
解答本题的关键是要明确成正比例关系的两个量比值一定。
13.√
【详解】
略
14.B
【分析】
判断两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;据此逐项分析后再选择。
【详解】
A.单价×数量=总价(一定),是积一定,所以单价和数量不成正比例;
B.因为圆的周长=圆周率×半径×2,周长÷半径=圆周率(一定)×2,所以圆的周长和半径成正比例;
C.小明的身高和年龄对应的比值或乘积都不一定,所以小明的身高和年龄不成比例;
D.平行四边形的面积=底×高,底和高的积一定,所以不成正比例。
故答案为:B。
【点睛】
此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
15.B
【分析】
根据xy=k(一定),x和y成反比例关系,进行选择。
【详解】
A.和的关系,不成比例关系;
B.乘积一定,成反比例关系;
C.比值一定,成正比例关系。
故答案为:B
【点睛】
关键是理解反比例的意义,积一定是反比例关系。
16.B
【分析】
两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的比值一定,即 =k(定值),那么这两个量叫做成正比例的量,它们的关系叫做正比例关系,由此判断即可;
【详解】
A.一个量变化,另一个量不变,不是正比例;
B. 一个量增加,另一个量也随着增加,成正比例;
C.一个量增加,另一个量随着减小,不成比例;
D. 一个量变化,另一个量不变,不是正比例;
故答案为:B
【点睛】
本题考查正比例图像的认识,需要熟练掌握正比例关系的特点,解答时注意,成正比例关系的图像就是一条经过原点的直线。
17.C
【分析】
根据(一定),x和y成正比例关系,进行选择。
【详解】
A. (一定),x和y不成比例关系;
B. (一定),x和y成反比例关系;
C. (一定),x和y成正比例关系。
故答案为:C
【点睛】
本题考查了辨识正比例的量,商一定是正比例关系,积一定是反比例关系。
18.B
【分析】
三角形的面积=底×高÷2,三角形的面积一定,说明底与高的乘积一定,根据反比例的意义可知,三角形的面积一定,它的底和高成反比例。
【详解】
根据分析可得,三角形的面积一定,它的底和高成反比例。
故答案为:B。
【点睛】
本题考查反比例的意义、三角形的面积,解答本题的关键是掌握反比例的意义。
19.
1 2 3 4 6 8 12 24 48
96 48 32 24 16 12 8 4 2
(1)h随着a的增加而减少;
(2)因为底×高=平行四边形的面积(一定),所以平行四边形底和高成反比例;
(3)6.4厘米
【分析】
(1)用面积÷底即可求出对应的高,,由此解答;
(2)平行四边形的面积=底×高,面积一定也是就是底和高乘反比例关系;据此解答;
(3)设高为x厘米,根据平行四边形的面积=底×高列出方程求解即可。
【详解】
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
填表如下:
1 2 3 4 6 8 12 24 48
96 48 32 24 16 12 8 4 2
(1)h随着a的增加而减少。
(2)因为底×高=平行四边形的面积(一定),所以平行四边形底和高成反比例。
(3)设高为厘米,
答:高是6.4厘米。
【点睛】
本题主要考查反比例关系的实际应用。
20.(1)
图上距离/cm 1 2 3 4 5 6 …
实际距离/km 30 60 90 120 150 180 …
(2)1∶3000000;正。
(3)450km。
【分析】
(1)看图可知:横轴为实际距离,纵轴为图上距离,再根据表中的数据一一对应在图中即可找出数值;(2)通过图上距离∶实际距离=比例尺即可求出;(3)通过图上距离÷比例尺=实际距离,代入数据即可求解。
【详解】
(1)看图填表。
图上距离/cm 1 2 3 4 5 6 …
实际距离/km 30 60 90 120 150 180 …
(2)30km=3000000cm,所以比例尺=1∶3000000。
故根据如图所示的图像可知,这幅地图的比例尺是(1∶3000000),图上距离和实际距离的比值一定,成( 正 )比例。
(3)实际距离:15÷=15×3000000=45000000(cm),45000000cm=45000000÷100000=450km。 故两地的实际距离为450km。
【点睛】
此题主要考查比例尺的应用以及提取图中信息的能力。
21.(1)见详解;(2)正;(3)37.5
【分析】
(1)根据统计表中的数据完成统计图。
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;由此解答即可。
(3)根据图象,观察纵轴5L所对应的横轴的数据,即可得出结论。
【详解】
(1)画图如下:
(2)15÷2=30÷4=45÷6=60÷8=7.5(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例。
(3)观察图表,这辆汽车耗油5升行37.5km。
【点评】
此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
22.(1)如图所示:
(2)14元
【分析】
根据数据描点连线;根据单价一定,求买7本书要多少钱。
【详解】
(1)根据数据描点连线,如图所示:
(2)单价=总价÷数量,笔记本的单价是一定的,所以7本笔记本需要:7×2=14元。
故答案为:(1)如图所示:
(2)14元。
【点睛】
本题考查反比例的意义,描点连线时是根据数量和总价所对应的的数描点,再把点按顺序连接起来。
答案第1页,共2页
答案第1页,共2页
