人教版八年级下册19.2.2 一次函数及应用课件(共27张PPT)
文档属性
| 名称 | 人教版八年级下册19.2.2 一次函数及应用课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 16:18:01 | ||
图片预览







文档简介
(共27张PPT)
课程:数学
《一次函数及应用》
人教版
八年级下册 第7课时
第 19 章 一次函数
教学目标
1
2
3
知识与技能
巩固一次函数知识,灵活运用变量关系解决相关实际问题。
过程与方法
有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力。
情感态度和价值观
认识数学在现实生活中的意义,提高运用数学知识解决实际问题的能力。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
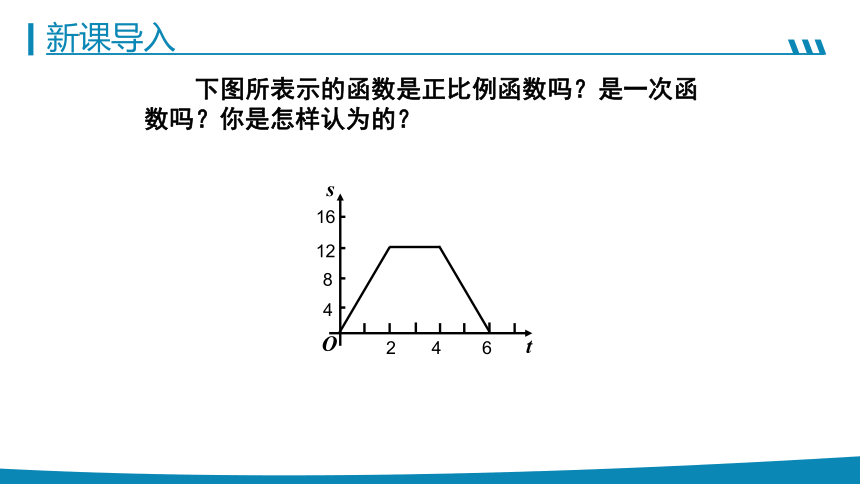
下图所表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
O
4
4
t
s
2
6
12
8
16
02
PART TWO
探究新知
Explore new knowledge
探究新知
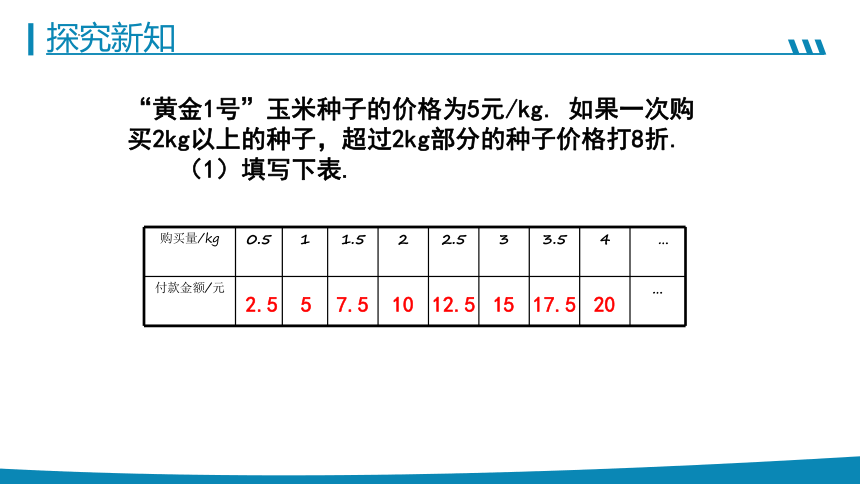
“黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(1)填写下表.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12.5
15
17.5
20
探究新知
“黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
解:设购买量为x千克,付款金额为y元.
当x>2时,
∴y=10+0.8 × 5(x-2)=4x+2.
当0≤x≤2时,
y=5x;
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12.5
15
17.5
20
探究新知
我们称此类函数为分段函数.
开始时引入图象所表示的是分段函数吗?你能写出它的解析式吗?说说你的做法.
O
4
4
t
s
2
6
12
8
16
s=6t;
0≤t≤2时,
2<t≤4时,
s=12;
4<t≤6时,
s=-6t+12.
探究新知
问题:为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .
0.9元/度
0.5元/度
O
探究新知
春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.
某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你根据图中信息,针对这种植物判断次日是否需要采取防霜冻措施,并说明理由.
O
x/时
y/ oC
探究新知
解:根据图象可知:
设0时~5时的一次函数关系式为y1=k1x+b1,
经过点(0,3),(5,-3),
b1=3,
5k1+b1=-3.
解得k1=-1.2,b1=3.
∴y1=-1.2x+3.
当y1、y2分别为0时,
而|x2-x1|= >3,
∴应采取防霜冻措施.
设5时~ 8时的一次函数关系式
为y2=k2x+b2,
经过点(5,-3),(8,5),
5k2+b2=-3 ,
8k2+b2=5.
解得 , .
∴ .
y/ oC
O
x/时
探究新知
例1 温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
探究新知
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
由已知条件,得
212k + b =100,
32k + b = 0 .
{
探究新知
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作
几小时?
解:(1)y = -5x + 40.
(2)8 h
探究新知
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x,(0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2.(x>8)
y=
探究新知
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
PART THREE
课堂练习
class exercise
03
课堂练习
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经
过几个月才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
课堂练习
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8
∴小明经过8个月才能存够200元
解得
∴
课堂练习
解:(1)由题意得
当0≤t≤2时,T=20;
当22.一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
函数解析式为:
T =
20(0≤t≤2)
5t+10(2{
课堂练习
20
10
40
T/℃
t/h
O
1
2
30
4
3
T=20(0≤t≤2)
T=5t+10(2(2)函数图像为:
课堂练习
3.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数解析式;
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
课堂练习
解:当0≤x≤50 时,由图象可设 y=k1x,∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;
当x>50时,由图象可设 y=k2x+b,∵其经过(50,25)、(100,70),得k2=0.9,b=-20,
∴y=0.9x-20.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
一次函数与实际问题
一次函数与实际问题
分段函数的解析式与图象
Thank you!
人教版
八年级下册
第 19 章 一次函数
课程:数学
《一次函数及应用》
人教版
八年级下册 第7课时
第 19 章 一次函数
教学目标
1
2
3
知识与技能
巩固一次函数知识,灵活运用变量关系解决相关实际问题。
过程与方法
有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力。
情感态度和价值观
认识数学在现实生活中的意义,提高运用数学知识解决实际问题的能力。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
下图所表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
O
4
4
t
s
2
6
12
8
16
02
PART TWO
探究新知
Explore new knowledge
探究新知
“黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(1)填写下表.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12.5
15
17.5
20
探究新知
“黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
解:设购买量为x千克,付款金额为y元.
当x>2时,
∴y=10+0.8 × 5(x-2)=4x+2.
当0≤x≤2时,
y=5x;
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12.5
15
17.5
20
探究新知
我们称此类函数为分段函数.
开始时引入图象所表示的是分段函数吗?你能写出它的解析式吗?说说你的做法.
O
4
4
t
s
2
6
12
8
16
s=6t;
0≤t≤2时,
2<t≤4时,
s=12;
4<t≤6时,
s=-6t+12.
探究新知
问题:为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .
0.9元/度
0.5元/度
O
探究新知
春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.
某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你根据图中信息,针对这种植物判断次日是否需要采取防霜冻措施,并说明理由.
O
x/时
y/ oC
探究新知
解:根据图象可知:
设0时~5时的一次函数关系式为y1=k1x+b1,
经过点(0,3),(5,-3),
b1=3,
5k1+b1=-3.
解得k1=-1.2,b1=3.
∴y1=-1.2x+3.
当y1、y2分别为0时,
而|x2-x1|= >3,
∴应采取防霜冻措施.
设5时~ 8时的一次函数关系式
为y2=k2x+b2,
经过点(5,-3),(8,5),
5k2+b2=-3 ,
8k2+b2=5.
解得 , .
∴ .
y/ oC
O
x/时
探究新知
例1 温度的度量有两种:摄氏温度和华氏温度.水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
探究新知
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
由已知条件,得
212k + b =100,
32k + b = 0 .
{
探究新知
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作
几小时?
解:(1)y = -5x + 40.
(2)8 h
探究新知
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x,(0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2.(x>8)
y=
探究新知
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
PART THREE
课堂练习
class exercise
03
课堂练习
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经
过几个月才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
课堂练习
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8
∴小明经过8个月才能存够200元
解得
∴
课堂练习
解:(1)由题意得
当0≤t≤2时,T=20;
当2
函数解析式为:
T =
20(0≤t≤2)
5t+10(2
课堂练习
20
10
40
T/℃
t/h
O
1
2
30
4
3
T=20(0≤t≤2)
T=5t+10(2
课堂练习
3.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数解析式;
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
课堂练习
解:当0≤x≤50 时,由图象可设 y=k1x,∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;
当x>50时,由图象可设 y=k2x+b,∵其经过(50,25)、(100,70),得k2=0.9,b=-20,
∴y=0.9x-20.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
一次函数与实际问题
一次函数与实际问题
分段函数的解析式与图象
Thank you!
人教版
八年级下册
第 19 章 一次函数
