2022-2023学年人教版七年级数学上册1.4.1有理数乘法 (第二课时)课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册1.4.1有理数乘法 (第二课时)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 22:09:47 | ||
图片预览








文档简介
(共22张PPT)
1.4.1 有理数的乘法运算律(第二课时)
1.4 有理数的乘除法
第一章 有理数
1,掌握有理数乘法运算律,并能进行熟练地运算.(重点)
学习目标
2,掌握多个有理数相乘的积的符号法则.(难点)
课前回顾
有理数乘法法则:
a.两数相乘,同号得正,异号得负,并把绝对值相乘.
b.任何数与0相乘,都得0.
c.运算步骤:先确定符号,再算绝对值的乘积.
d.带分数,小数相乘:先统一化成分数(假分数)或小数,再进行
乘法运算.
课前回顾
倒数:乘积是1的两个数互为倒数.
a,当a≠0时,a的倒数是
b,倒数是相互的,若a是b的倒数,则b是a的倒数,单独一个数不能称其为倒数
c,正数的倒数仍为的正数;负数的倒数仍为负数.0没有倒数.
d.倒数是它本身的有±1.
新课导入
思考1
观察下面的乘法算式,它们的乘积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5).
几个不是0的数相乘,积的符号与负因数的个数有什么关系?
归纳
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
新课导入
例3
计算
(1)(-3)××(-)×(-); (2) (-5)×6×(-)×
解:(1) (-3)××(-)×(-)
=-3×××
=-
(2) (-5)×6×(-)×
= 5×6××
=6
新课导入
思考2
你能看出下列的结果吗?如果能,请说明理由.
7.8×(-8.1)×0×(-19.6)
归纳
几个数相乘,如果其中有因数为0,那么积等于0.
出现0 积为0
新课导入
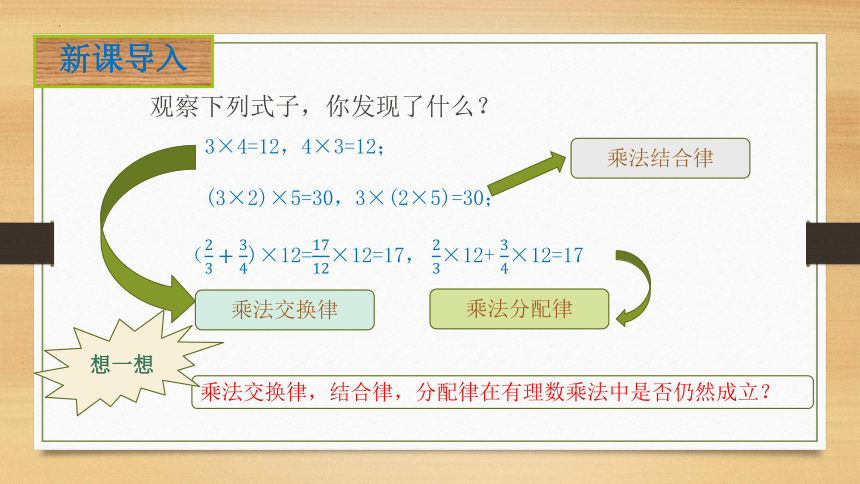
3×4=12,4×3=12;
(3×2)×5=30,3×(2×5)=30;
()×12=×12=17, ×12+ ×12=17
观察下列式子,你发现了什么?
乘法交换律,结合律,分配律在有理数乘法中是否仍然成立?
乘法交换律
乘法分配律
乘法结合律
想一想
新课导入
思考3
观察下面的乘法算式,你又能发现什么规律?
5×(-6)=-30; (-6)×5=-30.
我们发现:
5×(-6)=(-6)×5
归纳
因数位置改变,乘积不变
一般地,有理数乘法中,两个数相乘,交换有理数的位置,积相等.
乘法交换律:ab=ba
a×b也可以写为a·b或ab.当用字母表示乘数时,“×”号可以写为“·”或省略。
新课导入
思考4
观察下面的乘法算式,你又能发现什么规律?
[3×(-4)]×(-5)=(-12)×(-5)=60;
3×[(-4)×(-5)]=3×20=60.
我们发现:
[3×(-4)]×(-5)= 3×[(-4)×(-5)]
归纳
两两结合改变,乘积不变
一般地,有理数乘法中,三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
乘法结合律: (ab)c=a(bc).
新课导入
思考5
观察下面的乘法算式,你又能发现什么规律?
5×[3+(-7)]=5×(-4)=-20;
5×3+5×(-7)=15-30=-20.
我们发现:
5×[3+(-7)]= 5×3+5×(-7)
归纳
结果相等
一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律: a(b+c)=ab+ac.
先算和,再算积
先算积,再算和
例题讲解
用两种方法计算:(+-)×12
解法1:(+-)×12
=(+ )×12
= ×12
=-1
解法2:(+-)×12
= ×12+ ×12
=3+2-6
=-1
想一想
比较上面两种解法,它们在运算顺序上有什么区别?解法2用了什么运算律?哪种解法运算量小?
例题讲解
计算: ×(-16)×(-)×(-1)×8×(-0.25)
解:原式= -( ×16×××8× )
=-8
先确定符号
假分数,小数化为分数
例题讲解
计算: (-36)×(1-+ - )
解:原式= -36×1+36× -36× +36×
=-36+16-30+21
=-29
例题讲解
计算: -3.14×35.2+3.14×(-46.4)-3.14×18.4
解:原式= -3.14×(35.2+46.4+18.4)
=-3.14×100
=-314
想一想,为什么-46.4变成了46.4了?
例题讲解
计算: 99 ×(-6)
解:原式= (100-)×(-6)
=100×(-6)+ 6
=-600+
=-599
请问,这种解法运用了哪些乘法运算律?
试一试
99 ×2020
例题讲解
若(-2022)×63=P,则(-2022)×62的值可表示为( )
A.P-1 B.P+2022 C.P-2022 D.P+1
解析:(-2022)×63=P表示63个-2022相加的和为P,
那么62个-2022的和则为P-(-2022)=P+2022
B
例题讲解
如果4个不等的偶数m,n,p,q满足(3-m)(3-n)(3-p)(3-q)=9,求m+n+p+q得值.
解析:∵ m,n,p,q是四个不等得偶数
∴(3-m),(3-n),(3-p),(3-q)也是四个不等得数
且它们得乘积是9
又∵9是由1,-1,3和-3四个数相乘而得
∴ (3-m),(3-n),(3-p),(3-q)得得数分别为1,-1,3和-3
∴m,n,p,q四个数为2,4,0,6
∴m+n+p+q=2+4+0+6=12
例题讲解
计算: ( - -1)×(-24)
晓莉的计算过程如下:
解:原式= ×(-24)- ×(-24)-1×(-24) ①
=-14-20-24 ②
=-58 ③
请问晓莉的计算过程正确吗?如果不正确,请指出开始出错的步骤,并写出正确的计算过程.
×
解:原式= ×(-24)- ×(-24)-1×(-24)
=-14+20+24
=30
例题讲解
规定:符号“&”为选择两数中的负数,“◎”为选择两数中的非负数,例如:-1&2=-1;-1◎2=2;求(-4◎3)×(-5&2)的结果.
解:由题意得:(-4◎3)=3;(-5&2)=-5
∴(-4◎3)×(-5&2)=3×(-5)=-15
课后思考
已知=,则++值为多少?
已知a,b,c的积为负数,和为正数,且x=+++ ++,则x的值为多少?
课堂小结
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
几个数相乘,如果其中有因数为0,那么积等于0.
有理数乘法:
乘法交换律:两个数相乘,交换有理数的位置,积相等.即 ab=ba
有理数乘法运算律:
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.即(ab)c=a(bc).
乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.即a(b+c)=ab+ac.
1.4.1 有理数的乘法运算律(第二课时)
1.4 有理数的乘除法
第一章 有理数
1,掌握有理数乘法运算律,并能进行熟练地运算.(重点)
学习目标
2,掌握多个有理数相乘的积的符号法则.(难点)
课前回顾
有理数乘法法则:
a.两数相乘,同号得正,异号得负,并把绝对值相乘.
b.任何数与0相乘,都得0.
c.运算步骤:先确定符号,再算绝对值的乘积.
d.带分数,小数相乘:先统一化成分数(假分数)或小数,再进行
乘法运算.
课前回顾
倒数:乘积是1的两个数互为倒数.
a,当a≠0时,a的倒数是
b,倒数是相互的,若a是b的倒数,则b是a的倒数,单独一个数不能称其为倒数
c,正数的倒数仍为的正数;负数的倒数仍为负数.0没有倒数.
d.倒数是它本身的有±1.
新课导入
思考1
观察下面的乘法算式,它们的乘积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5).
几个不是0的数相乘,积的符号与负因数的个数有什么关系?
归纳
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
新课导入
例3
计算
(1)(-3)××(-)×(-); (2) (-5)×6×(-)×
解:(1) (-3)××(-)×(-)
=-3×××
=-
(2) (-5)×6×(-)×
= 5×6××
=6
新课导入
思考2
你能看出下列的结果吗?如果能,请说明理由.
7.8×(-8.1)×0×(-19.6)
归纳
几个数相乘,如果其中有因数为0,那么积等于0.
出现0 积为0
新课导入
3×4=12,4×3=12;
(3×2)×5=30,3×(2×5)=30;
()×12=×12=17, ×12+ ×12=17
观察下列式子,你发现了什么?
乘法交换律,结合律,分配律在有理数乘法中是否仍然成立?
乘法交换律
乘法分配律
乘法结合律
想一想
新课导入
思考3
观察下面的乘法算式,你又能发现什么规律?
5×(-6)=-30; (-6)×5=-30.
我们发现:
5×(-6)=(-6)×5
归纳
因数位置改变,乘积不变
一般地,有理数乘法中,两个数相乘,交换有理数的位置,积相等.
乘法交换律:ab=ba
a×b也可以写为a·b或ab.当用字母表示乘数时,“×”号可以写为“·”或省略。
新课导入
思考4
观察下面的乘法算式,你又能发现什么规律?
[3×(-4)]×(-5)=(-12)×(-5)=60;
3×[(-4)×(-5)]=3×20=60.
我们发现:
[3×(-4)]×(-5)= 3×[(-4)×(-5)]
归纳
两两结合改变,乘积不变
一般地,有理数乘法中,三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
乘法结合律: (ab)c=a(bc).
新课导入
思考5
观察下面的乘法算式,你又能发现什么规律?
5×[3+(-7)]=5×(-4)=-20;
5×3+5×(-7)=15-30=-20.
我们发现:
5×[3+(-7)]= 5×3+5×(-7)
归纳
结果相等
一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律: a(b+c)=ab+ac.
先算和,再算积
先算积,再算和
例题讲解
用两种方法计算:(+-)×12
解法1:(+-)×12
=(+ )×12
= ×12
=-1
解法2:(+-)×12
= ×12+ ×12
=3+2-6
=-1
想一想
比较上面两种解法,它们在运算顺序上有什么区别?解法2用了什么运算律?哪种解法运算量小?
例题讲解
计算: ×(-16)×(-)×(-1)×8×(-0.25)
解:原式= -( ×16×××8× )
=-8
先确定符号
假分数,小数化为分数
例题讲解
计算: (-36)×(1-+ - )
解:原式= -36×1+36× -36× +36×
=-36+16-30+21
=-29
例题讲解
计算: -3.14×35.2+3.14×(-46.4)-3.14×18.4
解:原式= -3.14×(35.2+46.4+18.4)
=-3.14×100
=-314
想一想,为什么-46.4变成了46.4了?
例题讲解
计算: 99 ×(-6)
解:原式= (100-)×(-6)
=100×(-6)+ 6
=-600+
=-599
请问,这种解法运用了哪些乘法运算律?
试一试
99 ×2020
例题讲解
若(-2022)×63=P,则(-2022)×62的值可表示为( )
A.P-1 B.P+2022 C.P-2022 D.P+1
解析:(-2022)×63=P表示63个-2022相加的和为P,
那么62个-2022的和则为P-(-2022)=P+2022
B
例题讲解
如果4个不等的偶数m,n,p,q满足(3-m)(3-n)(3-p)(3-q)=9,求m+n+p+q得值.
解析:∵ m,n,p,q是四个不等得偶数
∴(3-m),(3-n),(3-p),(3-q)也是四个不等得数
且它们得乘积是9
又∵9是由1,-1,3和-3四个数相乘而得
∴ (3-m),(3-n),(3-p),(3-q)得得数分别为1,-1,3和-3
∴m,n,p,q四个数为2,4,0,6
∴m+n+p+q=2+4+0+6=12
例题讲解
计算: ( - -1)×(-24)
晓莉的计算过程如下:
解:原式= ×(-24)- ×(-24)-1×(-24) ①
=-14-20-24 ②
=-58 ③
请问晓莉的计算过程正确吗?如果不正确,请指出开始出错的步骤,并写出正确的计算过程.
×
解:原式= ×(-24)- ×(-24)-1×(-24)
=-14+20+24
=30
例题讲解
规定:符号“&”为选择两数中的负数,“◎”为选择两数中的非负数,例如:-1&2=-1;-1◎2=2;求(-4◎3)×(-5&2)的结果.
解:由题意得:(-4◎3)=3;(-5&2)=-5
∴(-4◎3)×(-5&2)=3×(-5)=-15
课后思考
已知=,则++值为多少?
已知a,b,c的积为负数,和为正数,且x=+++ ++,则x的值为多少?
课堂小结
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
几个数相乘,如果其中有因数为0,那么积等于0.
有理数乘法:
乘法交换律:两个数相乘,交换有理数的位置,积相等.即 ab=ba
有理数乘法运算律:
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.即(ab)c=a(bc).
乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.即a(b+c)=ab+ac.
