人教版八年级下册18平行四边形复习课件(共31张PPT)
文档属性
| 名称 | 人教版八年级下册18平行四边形复习课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 06:35:16 | ||
图片预览








文档简介
(共31张PPT)
自主复习
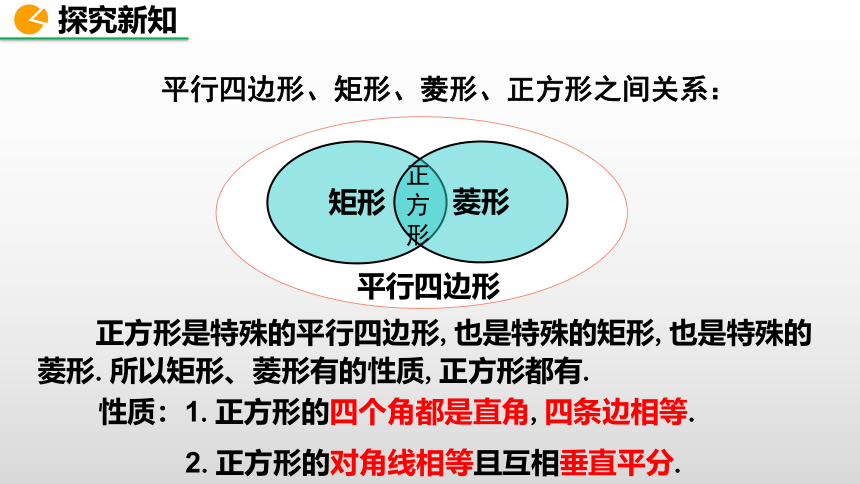
矩形
菱形
正方形
平行四边形
四边形
四边形及特殊四边形的关系
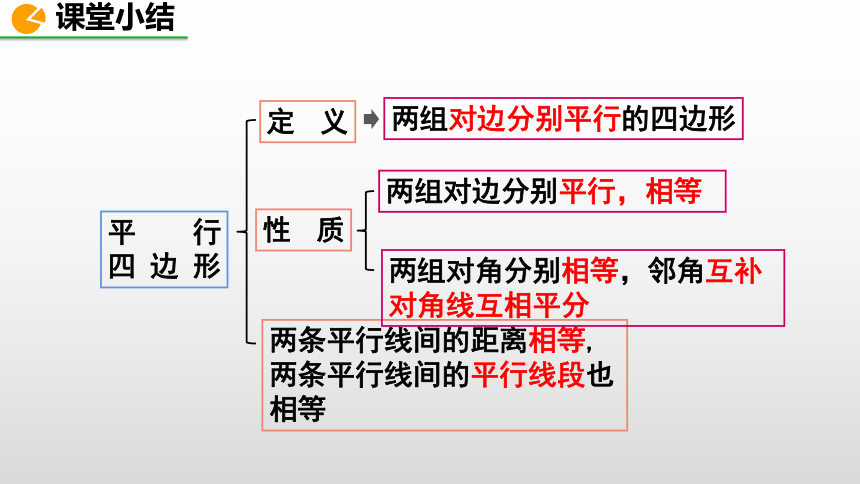
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
探究新知
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
总结:平行四边形、矩形、菱形、正方形的对称性
平行四边形
中心对称图形
(对角线的交点)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(四条)
探究新知
矩形
菱形
正方形
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线互相垂直
一组邻边相等
或对角线互相垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
探究新知
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的距离相等,
两条平行线间的平行线段也相等
两组对角分别相等,邻角互补
对角线互相平分
课堂小结
对角线互相平分的四边形是平行四边形.
判定
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
矩形的两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形的两条对角线相等
边
对角线
角
数学语言:
∵四边形ABCD是矩形,
∴AD ∥ BC ,CD ∥ AB.
∴AD =BC ,CD =AB.
∴AC= BD.
A
B
C
D
O
∴AO= CO ,OD = OB.
探究新知
矩形的性质
∴ ∠A=∠B=∠C=∠D=90°.
判定
对角线相等的平行四边形是矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
菱形的性质及有关计算
菱形的性质
有关计算
边
1.周长=边长的四倍;
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
判定
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
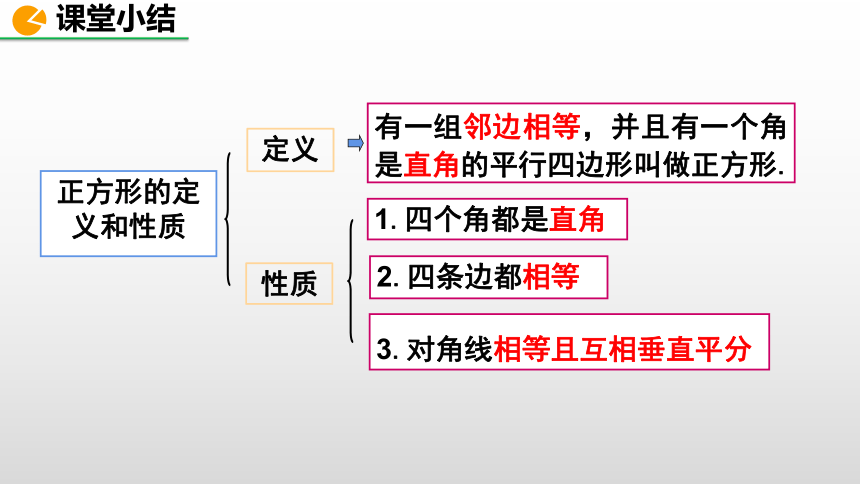
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的定义和性质
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
课堂小结
判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
对角线相互垂直的矩形是正方形.
对角线相等的菱形是正方形.
随堂演练
基础巩固
下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是( )
A.矩形 B.菱形 C.等腰梯形 D.正方形
D
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长是( )
A.1 B.2
C.1.5 D.3
B
D
基础巩固题
在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
A
D
B
C
D
课堂检测
如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为 ( )
A.6cm B.12cm C.4cm D.8cm
在□ABCD中, ∠A=3∠B, 求∠C和∠D 的度数 .
B
C
A
D
解:∵在□ABCD中, AD∥BC,
∴∠A+∠B= 180°.
又已知 ∠A=3∠B,
则 3∠B +∠B= 180°.
解得,∠B= 45°, ∠A=3×45°=135 °.
∴∠C=∠A=135 °, ∠D=∠B= 45°.
课堂检测
如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为_____.
2.5
如图,点E,F分别是矩形ABCD的边AB,CD上的点,且DF=BE.求证:AF=CE.
证明:∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=BC,
∴△ADF≌△CBE(SAS).
∴AF=CE.
AD=CB,
∠D=∠B,
DF=BE,
在△ADF和△CBE中,
如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
课堂检测
基础巩固题
若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
C
H
G
F
E
D
C
B
A
证明:连接AC , BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E , F , G , H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
探究新知
利用边相等判断四边形是菱形
∴ ,
如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30.
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,∴13h=120,得h= .
课堂检测
A
B
C
D
O
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;(2)菱形的面积.
解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC.
∴∠ABC+∠BAD=180°.
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC= ×180°=60°,∴∠ABO= ×∠ABC=30°.
∴△ABC是等边三角形.
课堂检测
能力提升题
O
A
B
C
D
∴OA= AB=1cm,AC=AB=2cm.
∴ .
∴BD=2OB= cm;
(2)S菱形ABCD = AC BD
= ×2×
= (cm2).
课堂检测
∵菱形ABCD的周长是8cm.
∴AB=2cm.
O
A
B
C
D
如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
C
如图,菱形ABCD的周长为48cm,对角线AC , BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
第3题图
第4题图
6cm
课堂检测
A
B
C
D
O
A
B
C
D
E
下列判断中正确的是( ) A.四边相等的四边形是正方形 B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
D
课堂检测
正方形具有而矩形不一定具有的性质是( )
A.四个角相等 B.对角线互相垂直平分
C.对角互补 D.对角线相等
正方形具有而菱形不一定具有的性质( )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
B
D
课堂检测
基础巩固题
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
D
课堂检测
B
D
A
C
如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,面积为AD2=8.
课堂检测
解:
A
D
B
C
O
如图,△ABC中,BD,CE为高,F是边BC的中点,判断△DEF的形状,并说明理由.
解:△DEF为等腰三角形.
在Rt△BEC中,∵F为BC的中点,
∴EF= BC.
同理:FD= BC.
∴FD=EF,
∴ △DEF为等腰三角形.
如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
课堂检测
拓广探索题
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5时四边形APQB是平行四边形.
课堂检测
解:由PD=(12-t)cm,CQ=2tcm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
课堂检测
自主复习
矩形
菱形
正方形
平行四边形
四边形
四边形及特殊四边形的关系
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
探究新知
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
总结:平行四边形、矩形、菱形、正方形的对称性
平行四边形
中心对称图形
(对角线的交点)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(四条)
探究新知
矩形
菱形
正方形
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线互相垂直
一组邻边相等
或对角线互相垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
探究新知
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的距离相等,
两条平行线间的平行线段也相等
两组对角分别相等,邻角互补
对角线互相平分
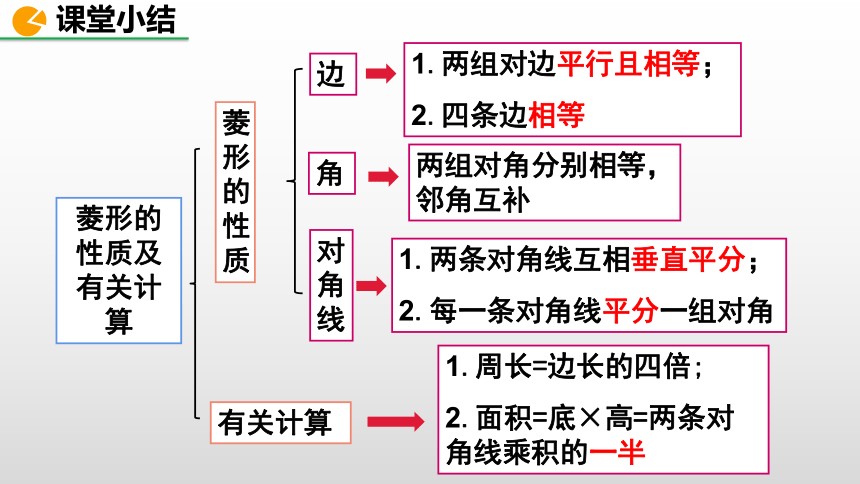
课堂小结
对角线互相平分的四边形是平行四边形.
判定
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
矩形的两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形的两条对角线相等
边
对角线
角
数学语言:
∵四边形ABCD是矩形,
∴AD ∥ BC ,CD ∥ AB.
∴AD =BC ,CD =AB.
∴AC= BD.
A
B
C
D
O
∴AO= CO ,OD = OB.
探究新知
矩形的性质
∴ ∠A=∠B=∠C=∠D=90°.
判定
对角线相等的平行四边形是矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
菱形的性质及有关计算
菱形的性质
有关计算
边
1.周长=边长的四倍;
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
判定
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的定义和性质
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
课堂小结
判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
对角线相互垂直的矩形是正方形.
对角线相等的菱形是正方形.
随堂演练
基础巩固
下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是( )
A.矩形 B.菱形 C.等腰梯形 D.正方形
D
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长是( )
A.1 B.2
C.1.5 D.3
B
D
基础巩固题
在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
A
D
B
C
D
课堂检测
如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为 ( )
A.6cm B.12cm C.4cm D.8cm
在□ABCD中, ∠A=3∠B, 求∠C和∠D 的度数 .
B
C
A
D
解:∵在□ABCD中, AD∥BC,
∴∠A+∠B= 180°.
又已知 ∠A=3∠B,
则 3∠B +∠B= 180°.
解得,∠B= 45°, ∠A=3×45°=135 °.
∴∠C=∠A=135 °, ∠D=∠B= 45°.
课堂检测
如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为_____.
2.5
如图,点E,F分别是矩形ABCD的边AB,CD上的点,且DF=BE.求证:AF=CE.
证明:∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=BC,
∴△ADF≌△CBE(SAS).
∴AF=CE.
AD=CB,
∠D=∠B,
DF=BE,
在△ADF和△CBE中,
如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
课堂检测
基础巩固题
若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
C
H
G
F
E
D
C
B
A
证明:连接AC , BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E , F , G , H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
探究新知
利用边相等判断四边形是菱形
∴ ,
如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30.
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,∴13h=120,得h= .
课堂检测
A
B
C
D
O
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;(2)菱形的面积.
解:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC.
∴∠ABC+∠BAD=180°.
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC= ×180°=60°,∴∠ABO= ×∠ABC=30°.
∴△ABC是等边三角形.
课堂检测
能力提升题
O
A
B
C
D
∴OA= AB=1cm,AC=AB=2cm.
∴ .
∴BD=2OB= cm;
(2)S菱形ABCD = AC BD
= ×2×
= (cm2).
课堂检测
∵菱形ABCD的周长是8cm.
∴AB=2cm.
O
A
B
C
D
如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
C
如图,菱形ABCD的周长为48cm,对角线AC , BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
第3题图
第4题图
6cm
课堂检测
A
B
C
D
O
A
B
C
D
E
下列判断中正确的是( ) A.四边相等的四边形是正方形 B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
D
课堂检测
正方形具有而矩形不一定具有的性质是( )
A.四个角相等 B.对角线互相垂直平分
C.对角互补 D.对角线相等
正方形具有而菱形不一定具有的性质( )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
B
D
课堂检测
基础巩固题
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
D
课堂检测
B
D
A
C
如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,面积为AD2=8.
课堂检测
解:
A
D
B
C
O
如图,△ABC中,BD,CE为高,F是边BC的中点,判断△DEF的形状,并说明理由.
解:△DEF为等腰三角形.
在Rt△BEC中,∵F为BC的中点,
∴EF= BC.
同理:FD= BC.
∴FD=EF,
∴ △DEF为等腰三角形.
如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
课堂检测
拓广探索题
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5时四边形APQB是平行四边形.
课堂检测
解:由PD=(12-t)cm,CQ=2tcm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
课堂检测
