人教版数学七年级上册课课练:4.3.2 角的比较与运算(word、含答案)
文档属性
| 名称 | 人教版数学七年级上册课课练:4.3.2 角的比较与运算(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 203.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 21:47:15 | ||
图片预览


文档简介
[角的比较与运算]
一、选择题
1.在∠AOB的内部任取一点C,作射线OC,则一定存在 ( )
A.∠AOB>∠AOC B.∠AOB<∠BOC
C.∠BOC>∠AOC D.∠AOC>∠BOC
2.已知∠α=76°5',∠β=76.5°,则∠α与∠β的大小关系是 ( )
A.∠α>∠β B.∠α=∠β
C.∠α<∠β D.以上都不对
3.[2020·深圳福田区期末] 射线OC在∠AOB内部,下列条件不能说明OC是∠AOB的平分线的是 ( )
A.∠AOC=∠AOB B.∠BOC=∠AOB
C.∠AOC+∠BOC=∠AOB D.∠AOC=∠BOC
4.如图,∠1=∠4,∠2=∠3,则下列说法不正确的是 ( )
A.∠AOE的平分线是射线OC
B.∠BOD的平分线是射线OC
C.∠AOC的平分线是射线OB
D.射线OC是∠AOE和∠BOD的平分线
5.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
A.50° B.75° C.100° D.20°
6.[2020·仁怀期末] 如图,用一副三角板可以画出15°的角,用它们还可以画出其他一些特殊角,下列角度中不能利用一副三角板直接画出的是 ( )
A.55° B.75° C.105° D.135°
7.如图,下列各式中错误的是 ( )
A.∠AOC=∠1+∠2
B.∠AOC=∠AOD-∠3
C.∠1+∠2=∠3
D.∠AOD-∠1-∠3=∠2
8.如图,若∠AOB=∠COD,则 ( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.∠1与∠2的大小关系不能确定
9.将一张长方形纸片折叠成如图所示的形状,则∠ABC的度数是 ( )
A.73° B.56° C.68° D.146°
10.已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为 ( )
A.28° B.112° C.28°或112° D.68°
二、填空题
11.如图所示,若∠AOC=90°,∠BOC=30°,则∠AOB= °;若∠AOD=20°,∠COD=50°,∠BOC=30°,则∠BOD= °,∠AOC= °,∠AOB= °.
12.如图,已知∠AOB=∠BOC=∠COD,则下列结论中正确的是 .(填序号即可)
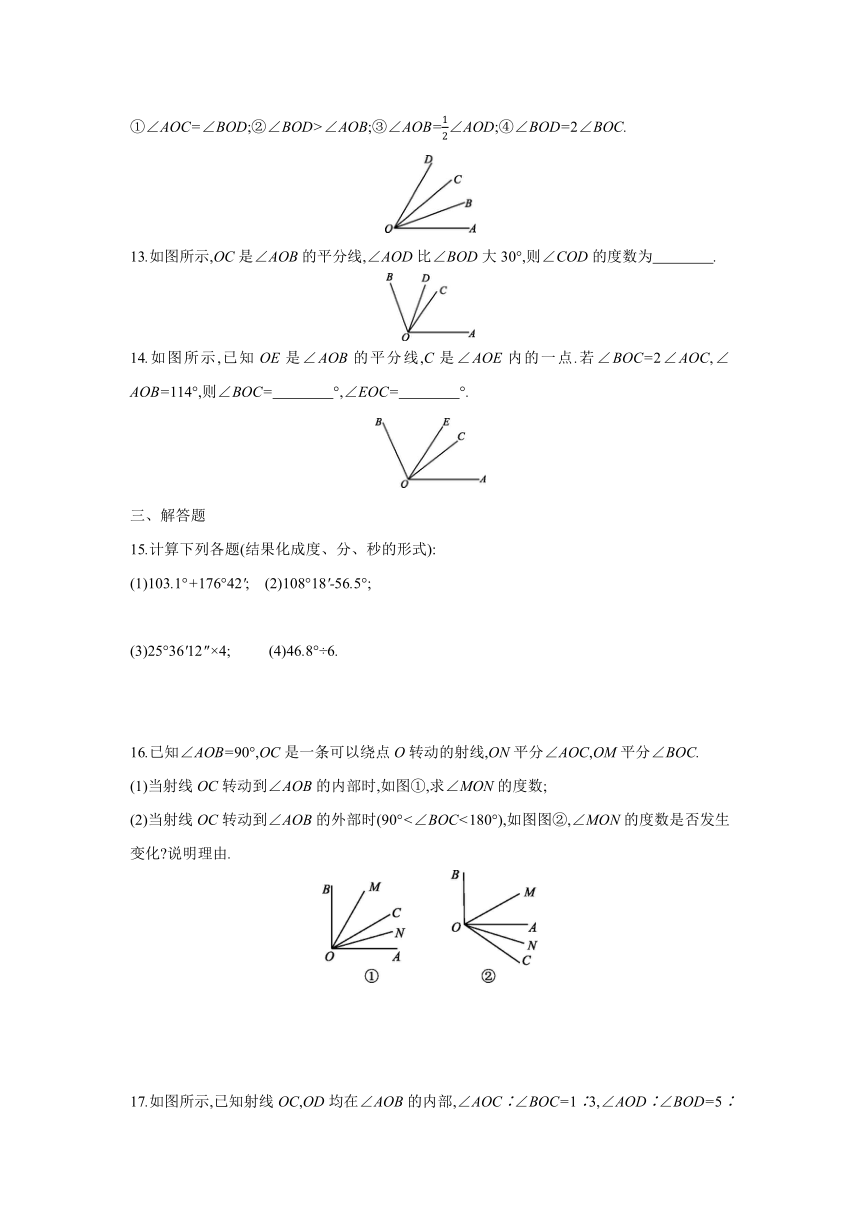
①∠AOC=∠BOD;②∠BOD>∠AOB;③∠AOB=∠AOD;④∠BOD=2∠BOC.
13.如图所示,OC是∠AOB的平分线,∠AOD比∠BOD大30°,则∠COD的度数为 .
14.如图所示,已知OE是∠AOB的平分线,C是∠AOE内的一点.若∠BOC=2∠AOC,∠AOB=114°,则∠BOC= °,∠EOC= °.
三、解答题
15.计算下列各题(结果化成度、分、秒的形式):
(1)103.1°+176°42'; (2)108°18'-56.5°;
(3)25°36'12″×4; (4)46.8°÷6.
16.已知∠AOB=90°,OC是一条可以绕点O转动的射线,ON平分∠AOC,OM平分∠BOC.
(1)当射线OC转动到∠AOB的内部时,如图①,求∠MON的度数;
(2)当射线OC转动到∠AOB的外部时(90°<∠BOC<180°),如图图②,∠MON的度数是否发生变化 说明理由.
17.如图所示,已知射线OC,OD均在∠AOB的内部,∠AOC∶∠BOC=1∶3,∠AOD∶∠BOD=5∶7.若∠COD=15°,求∠AOB的度数.
[转化思想] O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一块三角尺的直角顶点放在点O处.
(1)如图①,将三角尺MON的一边ON与射线OB重合,则∠MOC= °;
(2)将三角尺MON绕点O逆时针旋转至图②的位置,此时OC是∠MOB的平分线,求∠BON和∠CON的度数;
(3)将三角尺MON绕点O逆时针旋转至图③的位置时,∠NOC=∠AOM,求∠NOB的度数.
答案
[课堂达标]
1.A 2.C 3.C 4.C 5.C 6.A
7.C 因为OC不一定是∠AOD的平分线,所以结论∠1+∠2=∠3不一定成立,即C中的式子是错误的.故选C.
8.B 因为∠AOB=∠COD,即∠1+∠DOB=∠2+∠DOB,所以∠1=∠2.
9.A
10.C 如图图,若射线OC与射线OC1重合,
则∠BOC=∠AOB-∠AOC=70°-42°=28°;
若射线OC与射线OC2重合,则∠BOC=∠AOB+∠AOC=70°+42°=112°.故选C.
11.120 80 70 100 若∠AOC=90°,∠BOC=30°,则∠AOB=∠AOC+∠BOC=90°+30°=120°.若∠AOD=20°,∠COD=50°,∠BOC=30°,则∠BOD=∠COD+∠BOC=50°+30°=80°;∠AOC=∠AOD+∠COD=20°+50°=70°;∠AOB=∠AOD+∠COD+∠BOC=20°+50°+30°=100°.
12.①②④
13.15° 设∠BOD=x,则∠AOD=x+30°,∠AOB=2x+30°.因为OC是∠AOB的平分线,所以∠AOC=∠AOB.所以∠COD=∠AOD-∠AOC=∠AOD-∠AOB=x+30°-(2x+30°)=15°.
14.76 19 因为OE是∠AOB的平分线,
∠AOB=114°,
所以∠BOE=∠AOB =×114°=57°.
因为∠BOC=2∠AOC,∠AOB=114°,
所以∠BOC=114°×=76°.
所以∠EOC=∠BOC-∠BOE=19°.
15.解:(1)103.1°+176°42'=103°6'+176°42'=
279°48'.
(2)108°18'-56.5°=108°18'-56°30'=51°48'.
(3)25°36'12″×4=100°144'48″=102°24'48″.
(4)46.8°÷6=7.8°=7°48'.
16.解:(1)因为ON平分∠AOC,OM平分∠BOC,
所以∠NOC=∠AOC,∠MOC=∠BOC.
所以∠MON=∠MOC+∠NOC=∠BOC+∠AOC=∠AOB=45°.
(2)∠MON的度数不发生变化,仍然是45°.
理由如图下:
因为ON平分∠AOC,OM平分∠BOC,
所以∠NOC=∠AOC,∠MOC=∠BOC.
所以∠MON=∠MOC-∠NOC=∠BOC-∠AOC=∠AOB=45°.
17. 把求∠AOB的度数转化为解一元一次方程.
解:设∠AOB的度数为x.
因为∠AOC∶∠BOC=1∶3,
所以∠AOC=x.
因为∠AOD∶∠BOD=5∶7,
所以∠AOD=x.
又因为∠COD=∠AOD-∠AOC,∠COD=15°,
所以15°=x-x,解得x=90°,
即∠AOB的度数为90°.
[素养提升]
解:(1)因为∠MON=90°,∠BOC=65°,
所以∠MOC=∠MON-∠BOC=90°-65°=25°.故答案为25.
(2)因为∠BOC=65°,OC是∠MOB的平分线,
所以∠MOB=2∠BOC=130°.
所以∠BON=∠MOB-∠MON=130°-90°=40°.
所以∠CON=∠BOC-∠BON=65°-40°=25°.
(3)因为∠BOC=65°,
所以∠AOC=∠AOB-∠BOC=180°-65°=115°.
因为∠MON=90°,
所以∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°.
又因为∠NOC=∠AOM,
所以2∠NOC=25°.
所以∠NOC=12.5°.
所以∠NOB=∠NOC+∠BOC=77.5°.
一、选择题
1.在∠AOB的内部任取一点C,作射线OC,则一定存在 ( )
A.∠AOB>∠AOC B.∠AOB<∠BOC
C.∠BOC>∠AOC D.∠AOC>∠BOC
2.已知∠α=76°5',∠β=76.5°,则∠α与∠β的大小关系是 ( )
A.∠α>∠β B.∠α=∠β
C.∠α<∠β D.以上都不对
3.[2020·深圳福田区期末] 射线OC在∠AOB内部,下列条件不能说明OC是∠AOB的平分线的是 ( )
A.∠AOC=∠AOB B.∠BOC=∠AOB
C.∠AOC+∠BOC=∠AOB D.∠AOC=∠BOC
4.如图,∠1=∠4,∠2=∠3,则下列说法不正确的是 ( )
A.∠AOE的平分线是射线OC
B.∠BOD的平分线是射线OC
C.∠AOC的平分线是射线OB
D.射线OC是∠AOE和∠BOD的平分线
5.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
A.50° B.75° C.100° D.20°
6.[2020·仁怀期末] 如图,用一副三角板可以画出15°的角,用它们还可以画出其他一些特殊角,下列角度中不能利用一副三角板直接画出的是 ( )
A.55° B.75° C.105° D.135°
7.如图,下列各式中错误的是 ( )
A.∠AOC=∠1+∠2
B.∠AOC=∠AOD-∠3
C.∠1+∠2=∠3
D.∠AOD-∠1-∠3=∠2
8.如图,若∠AOB=∠COD,则 ( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.∠1与∠2的大小关系不能确定
9.将一张长方形纸片折叠成如图所示的形状,则∠ABC的度数是 ( )
A.73° B.56° C.68° D.146°
10.已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为 ( )
A.28° B.112° C.28°或112° D.68°
二、填空题
11.如图所示,若∠AOC=90°,∠BOC=30°,则∠AOB= °;若∠AOD=20°,∠COD=50°,∠BOC=30°,则∠BOD= °,∠AOC= °,∠AOB= °.
12.如图,已知∠AOB=∠BOC=∠COD,则下列结论中正确的是 .(填序号即可)
①∠AOC=∠BOD;②∠BOD>∠AOB;③∠AOB=∠AOD;④∠BOD=2∠BOC.
13.如图所示,OC是∠AOB的平分线,∠AOD比∠BOD大30°,则∠COD的度数为 .
14.如图所示,已知OE是∠AOB的平分线,C是∠AOE内的一点.若∠BOC=2∠AOC,∠AOB=114°,则∠BOC= °,∠EOC= °.
三、解答题
15.计算下列各题(结果化成度、分、秒的形式):
(1)103.1°+176°42'; (2)108°18'-56.5°;
(3)25°36'12″×4; (4)46.8°÷6.
16.已知∠AOB=90°,OC是一条可以绕点O转动的射线,ON平分∠AOC,OM平分∠BOC.
(1)当射线OC转动到∠AOB的内部时,如图①,求∠MON的度数;
(2)当射线OC转动到∠AOB的外部时(90°<∠BOC<180°),如图图②,∠MON的度数是否发生变化 说明理由.
17.如图所示,已知射线OC,OD均在∠AOB的内部,∠AOC∶∠BOC=1∶3,∠AOD∶∠BOD=5∶7.若∠COD=15°,求∠AOB的度数.
[转化思想] O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一块三角尺的直角顶点放在点O处.
(1)如图①,将三角尺MON的一边ON与射线OB重合,则∠MOC= °;
(2)将三角尺MON绕点O逆时针旋转至图②的位置,此时OC是∠MOB的平分线,求∠BON和∠CON的度数;
(3)将三角尺MON绕点O逆时针旋转至图③的位置时,∠NOC=∠AOM,求∠NOB的度数.
答案
[课堂达标]
1.A 2.C 3.C 4.C 5.C 6.A
7.C 因为OC不一定是∠AOD的平分线,所以结论∠1+∠2=∠3不一定成立,即C中的式子是错误的.故选C.
8.B 因为∠AOB=∠COD,即∠1+∠DOB=∠2+∠DOB,所以∠1=∠2.
9.A
10.C 如图图,若射线OC与射线OC1重合,
则∠BOC=∠AOB-∠AOC=70°-42°=28°;
若射线OC与射线OC2重合,则∠BOC=∠AOB+∠AOC=70°+42°=112°.故选C.
11.120 80 70 100 若∠AOC=90°,∠BOC=30°,则∠AOB=∠AOC+∠BOC=90°+30°=120°.若∠AOD=20°,∠COD=50°,∠BOC=30°,则∠BOD=∠COD+∠BOC=50°+30°=80°;∠AOC=∠AOD+∠COD=20°+50°=70°;∠AOB=∠AOD+∠COD+∠BOC=20°+50°+30°=100°.
12.①②④
13.15° 设∠BOD=x,则∠AOD=x+30°,∠AOB=2x+30°.因为OC是∠AOB的平分线,所以∠AOC=∠AOB.所以∠COD=∠AOD-∠AOC=∠AOD-∠AOB=x+30°-(2x+30°)=15°.
14.76 19 因为OE是∠AOB的平分线,
∠AOB=114°,
所以∠BOE=∠AOB =×114°=57°.
因为∠BOC=2∠AOC,∠AOB=114°,
所以∠BOC=114°×=76°.
所以∠EOC=∠BOC-∠BOE=19°.
15.解:(1)103.1°+176°42'=103°6'+176°42'=
279°48'.
(2)108°18'-56.5°=108°18'-56°30'=51°48'.
(3)25°36'12″×4=100°144'48″=102°24'48″.
(4)46.8°÷6=7.8°=7°48'.
16.解:(1)因为ON平分∠AOC,OM平分∠BOC,
所以∠NOC=∠AOC,∠MOC=∠BOC.
所以∠MON=∠MOC+∠NOC=∠BOC+∠AOC=∠AOB=45°.
(2)∠MON的度数不发生变化,仍然是45°.
理由如图下:
因为ON平分∠AOC,OM平分∠BOC,
所以∠NOC=∠AOC,∠MOC=∠BOC.
所以∠MON=∠MOC-∠NOC=∠BOC-∠AOC=∠AOB=45°.
17. 把求∠AOB的度数转化为解一元一次方程.
解:设∠AOB的度数为x.
因为∠AOC∶∠BOC=1∶3,
所以∠AOC=x.
因为∠AOD∶∠BOD=5∶7,
所以∠AOD=x.
又因为∠COD=∠AOD-∠AOC,∠COD=15°,
所以15°=x-x,解得x=90°,
即∠AOB的度数为90°.
[素养提升]
解:(1)因为∠MON=90°,∠BOC=65°,
所以∠MOC=∠MON-∠BOC=90°-65°=25°.故答案为25.
(2)因为∠BOC=65°,OC是∠MOB的平分线,
所以∠MOB=2∠BOC=130°.
所以∠BON=∠MOB-∠MON=130°-90°=40°.
所以∠CON=∠BOC-∠BON=65°-40°=25°.
(3)因为∠BOC=65°,
所以∠AOC=∠AOB-∠BOC=180°-65°=115°.
因为∠MON=90°,
所以∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°.
又因为∠NOC=∠AOM,
所以2∠NOC=25°.
所以∠NOC=12.5°.
所以∠NOB=∠NOC+∠BOC=77.5°.
