人教版数学七年级上册阶段练习 第四章 几何图形初步 综合检测(word、含答案)
文档属性
| 名称 | 人教版数学七年级上册阶段练习 第四章 几何图形初步 综合检测(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 222.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 22:23:10 | ||
图片预览


文档简介
第四章综合检测
几何图形初步
一、选择题(本大题共10小题,每小题3分,共30分)
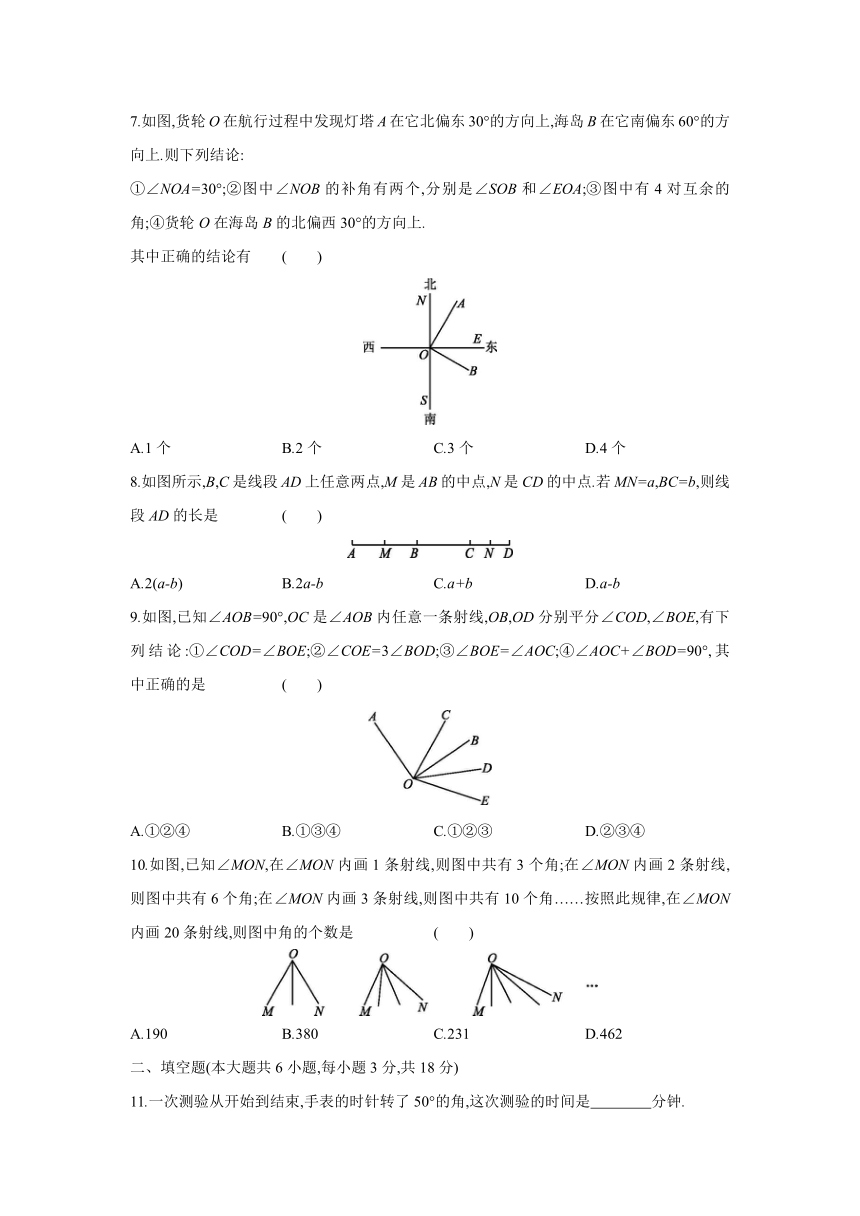
1.在下列几何体中,有 个棱柱 ( )
A.1 B.2 C.3 D.4
2.下列几何体中可以由平面图形绕某条直线旋转一周得到的是 ( )
3.有下列说法:①经过一点有无数条直线;②两点之间,线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为 ( )
A.1 B.2 C.3 D.4
4.有下列日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某个同学的跳远成绩;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是 ( )
A.①④ B.②③ C.③ D.④
5.下列四个图形中,不能作为正方体的展开图的是 ( )
6.把一副三角尺ABC与BDE按如图所示方式拼在一起,其中A,B,D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是 ( )
A.60° B.67.5° C.75° D.85°
7.如图,货轮O在航行过程中发现灯塔A在它北偏东30°的方向上,海岛B在它南偏东60°的方向上.则下列结论:
①∠NOA=30°;②图中∠NOB的补角有两个,分别是∠SOB和∠EOA;③图中有4对互余的角;④货轮O在海岛B的北偏西30°的方向上.
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图所示,B,C是线段AD上任意两点,M是AB的中点,N是CD的中点.若MN=a,BC=b,则线段AD的长是 ( )
A.2(a-b) B.2a-b C.a+b D.a-b
9.如图,已知∠AOB=90°,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,有下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC+∠BOD=90°,其中正确的是 ( )
A.①②④ B.①③④ C.①②③ D.②③④
10.如图,已知∠MON,在∠MON内画1条射线,则图中共有3个角;在∠MON内画2条射线,则图中共有6个角;在∠MON内画3条射线,则图中共有10个角……按照此规律,在∠MON内画20条射线,则图中角的个数是 ( )
A.190 B.380 C.231 D.462
二、填空题(本大题共6小题,每小题3分,共18分)
11.一次测验从开始到结束,手表的时针转了50°的角,这次测验的时间是 分钟.
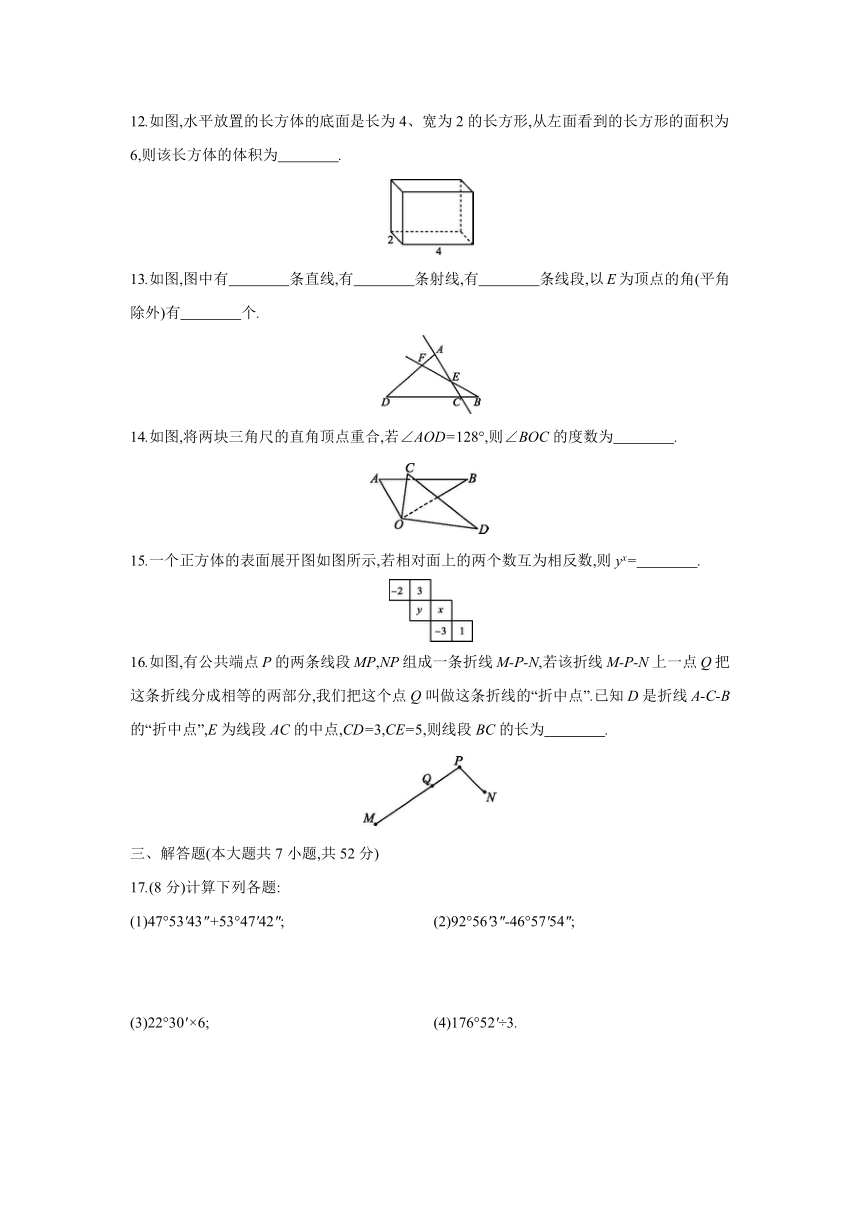
12.如图,水平放置的长方体的底面是长为4、宽为2的长方形,从左面看到的长方形的面积为6,则该长方体的体积为 .
13.如图,图中有 条直线,有 条射线,有 条线段,以E为顶点的角(平角除外)有 个.
14.如图,将两块三角尺的直角顶点重合,若∠AOD=128°,则∠BOC的度数为 .
15.一个正方体的表面展开图如图所示,若相对面上的两个数互为相反数,则yx= .
16.如图,有公共端点P的两条线段MP,NP组成一条折线M-P-N,若该折线M-P-N上一点Q把这条折线分成相等的两部分,我们把这个点Q叫做这条折线的“折中点”.已知D是折线A-C-B的“折中点”,E为线段AC的中点,CD=3,CE=5,则线段BC的长为 .
三、解答题(本大题共7小题,共52分)
17.(8分)计算下列各题:
(1)47°53'43″+53°47'42″; (2)92°56'3″-46°57'54″;
(3)22°30'×6; (4)176°52'÷3.
18.(6分)如图是由5个棱长为1的正方体组成的几何体.
(1)该几何体的体积是 ,表面积是 ;
(2)画出从正面看和从左面看该几何体得到的图形.
19.(6分)点A,B,C,D的位置如图,按下列要求画出图形:
(1)画直线AB,直线CD,它们相交于点E;
(2)连接AC,BD,它们相交于点O;
(3)画射线AD,射线BC,它们交于点F.
20.(8分)已知:如图,B,C是线段AD上的两点,且AB∶BC∶CD=2∶4∶3,M是AD的中点,CD=9 cm,求线段MC的长.
21.(8分)一只电子跳蚤从点O出发,沿南偏东60°方向跳了1.5 cm到达点A,再从点A开始沿北偏东30°方向跳了2 cm到达点B,最后由点B回到点O.
(1)在中画出电子跳蚤所跳的路线图(比例尺为1∶1);
(2)量一量,OB大约长多少厘米
22.(8分)如图,O是直线AB上任意一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠BOD互补的角有 ;
(2)若∠COD=26°,求∠DOE的度数;
(3)当∠BOE=α时,请求出∠DOE的度数.
23.(8分)如图①,已知线段AB=30 cm,CD=4 cm,线段CD在线段AB上运动,E,F分别是AC,BD的中点.
(1)若AC=8 cm,则EF= cm.
(2)①当线段CD在线段AB上运动时,试判断EF的长度是否发生变化.如图果不变,请求出EF的长度;如图果变化,请说明理由.
②我们发现角的很多规律和线段一样,如图②,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD,则∠EOF,∠AOB和∠COD有何数量关系 请直接写出结果,不需说明理由.
答案
1.B 2.B 3.C
4.A 5.D 6.C
7.D 8.B
9.A 10.C
11.100 12.24
13.1 9 12 4
14.52° 15.1
16.4或16
17.(1)101°41'25″ (2)45°58'9″ (3)135°
(4)58°57'20″
18.解:(1)5 22
(2)如图图所示:
19.解:(1)如图图所示.
(2)如图图所示.
(3)如图图所示.
20.解:因为AB∶BC∶CD=2∶4∶3,
所以设AB=2x cm,BC=4x cm,CD=3x cm.
所以3x=9,解得x=3.
所以AB=6 cm,BC=12 cm.
所以AD=AB+BC+CD=6+12+9=27(cm).
又因为M是AD的中点,
所以MD=AD=13.5(cm).
所以MC=MD-CD=13.5-9=4.5(cm).
21.解:(1)如图图所示:
(2)2.5 cm.
22.解:(1)∠AOD,∠COD
(2)因为OD,OE分别平分∠AOC,∠BOC,
所以∠AOC=2∠COD=52°.
所以∠BOC=180°-∠AOC=128°.
所以∠COE=∠BOC=64°.
所以∠DOE=∠COD+∠COE=26°+64°=90°.
(3)因为OD,OE分别平分∠AOC和∠BOC,
所以∠DOE=∠COD+∠COE=∠AOC+∠BOC=(∠AOC+∠BOC)=×180°=90°.
所以当∠BOE=α时,∠DOE=90°.
23.解:(1)17
(2)①EF的长度不变.
因为E,F分别是AC,BD的中点,
所以EC=AC,DF=BD.
所以EF=EC+CD+DF=AC+CD+BD
=(AC+BD)+CD=(AB-CD)+CD
=(AB+CD)=17 cm.
②∠EOF=(∠AOB+∠COD).
几何图形初步
一、选择题(本大题共10小题,每小题3分,共30分)
1.在下列几何体中,有 个棱柱 ( )
A.1 B.2 C.3 D.4
2.下列几何体中可以由平面图形绕某条直线旋转一周得到的是 ( )
3.有下列说法:①经过一点有无数条直线;②两点之间,线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为 ( )
A.1 B.2 C.3 D.4
4.有下列日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某个同学的跳远成绩;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是 ( )
A.①④ B.②③ C.③ D.④
5.下列四个图形中,不能作为正方体的展开图的是 ( )
6.把一副三角尺ABC与BDE按如图所示方式拼在一起,其中A,B,D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是 ( )
A.60° B.67.5° C.75° D.85°
7.如图,货轮O在航行过程中发现灯塔A在它北偏东30°的方向上,海岛B在它南偏东60°的方向上.则下列结论:
①∠NOA=30°;②图中∠NOB的补角有两个,分别是∠SOB和∠EOA;③图中有4对互余的角;④货轮O在海岛B的北偏西30°的方向上.
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图所示,B,C是线段AD上任意两点,M是AB的中点,N是CD的中点.若MN=a,BC=b,则线段AD的长是 ( )
A.2(a-b) B.2a-b C.a+b D.a-b
9.如图,已知∠AOB=90°,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,有下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC+∠BOD=90°,其中正确的是 ( )
A.①②④ B.①③④ C.①②③ D.②③④
10.如图,已知∠MON,在∠MON内画1条射线,则图中共有3个角;在∠MON内画2条射线,则图中共有6个角;在∠MON内画3条射线,则图中共有10个角……按照此规律,在∠MON内画20条射线,则图中角的个数是 ( )
A.190 B.380 C.231 D.462
二、填空题(本大题共6小题,每小题3分,共18分)
11.一次测验从开始到结束,手表的时针转了50°的角,这次测验的时间是 分钟.
12.如图,水平放置的长方体的底面是长为4、宽为2的长方形,从左面看到的长方形的面积为6,则该长方体的体积为 .
13.如图,图中有 条直线,有 条射线,有 条线段,以E为顶点的角(平角除外)有 个.
14.如图,将两块三角尺的直角顶点重合,若∠AOD=128°,则∠BOC的度数为 .
15.一个正方体的表面展开图如图所示,若相对面上的两个数互为相反数,则yx= .
16.如图,有公共端点P的两条线段MP,NP组成一条折线M-P-N,若该折线M-P-N上一点Q把这条折线分成相等的两部分,我们把这个点Q叫做这条折线的“折中点”.已知D是折线A-C-B的“折中点”,E为线段AC的中点,CD=3,CE=5,则线段BC的长为 .
三、解答题(本大题共7小题,共52分)
17.(8分)计算下列各题:
(1)47°53'43″+53°47'42″; (2)92°56'3″-46°57'54″;
(3)22°30'×6; (4)176°52'÷3.
18.(6分)如图是由5个棱长为1的正方体组成的几何体.
(1)该几何体的体积是 ,表面积是 ;
(2)画出从正面看和从左面看该几何体得到的图形.
19.(6分)点A,B,C,D的位置如图,按下列要求画出图形:
(1)画直线AB,直线CD,它们相交于点E;
(2)连接AC,BD,它们相交于点O;
(3)画射线AD,射线BC,它们交于点F.
20.(8分)已知:如图,B,C是线段AD上的两点,且AB∶BC∶CD=2∶4∶3,M是AD的中点,CD=9 cm,求线段MC的长.
21.(8分)一只电子跳蚤从点O出发,沿南偏东60°方向跳了1.5 cm到达点A,再从点A开始沿北偏东30°方向跳了2 cm到达点B,最后由点B回到点O.
(1)在中画出电子跳蚤所跳的路线图(比例尺为1∶1);
(2)量一量,OB大约长多少厘米
22.(8分)如图,O是直线AB上任意一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠BOD互补的角有 ;
(2)若∠COD=26°,求∠DOE的度数;
(3)当∠BOE=α时,请求出∠DOE的度数.
23.(8分)如图①,已知线段AB=30 cm,CD=4 cm,线段CD在线段AB上运动,E,F分别是AC,BD的中点.
(1)若AC=8 cm,则EF= cm.
(2)①当线段CD在线段AB上运动时,试判断EF的长度是否发生变化.如图果不变,请求出EF的长度;如图果变化,请说明理由.
②我们发现角的很多规律和线段一样,如图②,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD,则∠EOF,∠AOB和∠COD有何数量关系 请直接写出结果,不需说明理由.
答案
1.B 2.B 3.C
4.A 5.D 6.C
7.D 8.B
9.A 10.C
11.100 12.24
13.1 9 12 4
14.52° 15.1
16.4或16
17.(1)101°41'25″ (2)45°58'9″ (3)135°
(4)58°57'20″
18.解:(1)5 22
(2)如图图所示:
19.解:(1)如图图所示.
(2)如图图所示.
(3)如图图所示.
20.解:因为AB∶BC∶CD=2∶4∶3,
所以设AB=2x cm,BC=4x cm,CD=3x cm.
所以3x=9,解得x=3.
所以AB=6 cm,BC=12 cm.
所以AD=AB+BC+CD=6+12+9=27(cm).
又因为M是AD的中点,
所以MD=AD=13.5(cm).
所以MC=MD-CD=13.5-9=4.5(cm).
21.解:(1)如图图所示:
(2)2.5 cm.
22.解:(1)∠AOD,∠COD
(2)因为OD,OE分别平分∠AOC,∠BOC,
所以∠AOC=2∠COD=52°.
所以∠BOC=180°-∠AOC=128°.
所以∠COE=∠BOC=64°.
所以∠DOE=∠COD+∠COE=26°+64°=90°.
(3)因为OD,OE分别平分∠AOC和∠BOC,
所以∠DOE=∠COD+∠COE=∠AOC+∠BOC=(∠AOC+∠BOC)=×180°=90°.
所以当∠BOE=α时,∠DOE=90°.
23.解:(1)17
(2)①EF的长度不变.
因为E,F分别是AC,BD的中点,
所以EC=AC,DF=BD.
所以EF=EC+CD+DF=AC+CD+BD
=(AC+BD)+CD=(AB-CD)+CD
=(AB+CD)=17 cm.
②∠EOF=(∠AOB+∠COD).
