人教版高中物理选择性必修第一册 1.2 动量定理 课件(23张PPT)
文档属性
| 名称 | 人教版高中物理选择性必修第一册 1.2 动量定理 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-23 05:38:04 | ||
图片预览








文档简介
(共23张PPT)
人教版 / 高中 / 物理
1.2 动量定理
让粉笔从相同的高度分别落到水泥地上和铺在地上的厚布上,观察会有怎样的现象发生。
结果:落在水泥地上的粉笔断了,而落在垫有厚布的地上却没有断。
演示实验:粉笔落地
导入新课
思考:为什么会产生这两种不同的现象?
在前面所学的动能定理中,我们知道,动能的变化是由于力的位移积累即力做功的结果,那么,动量的变化又是什么原因引起的呢?
温故知新
探究新知
汽车以速度V运动,急刹车到停止。若对车施加很大的阻力,则车停止时间很短;如果对车施加很小的阻力,则车停止时间较长。
两种情况下,汽车的_______变化相同。可见,引起运动状态改变,要考虑_______和_________这两个因素。
情境探究
动量
受力
时间
f1
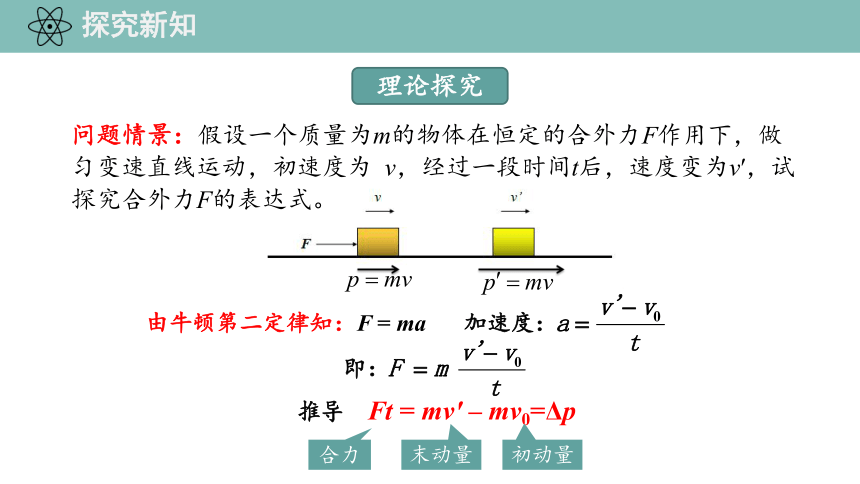
探究新知
问题情景:假设一个质量为m的物体在恒定的合外力F作用下,做匀变速直线运动,初速度为 v,经过一段时间t后,速度变为v′,试探究合外力F的表达式。
理论探究
由牛顿第二定律知:F = ma
加速度:
推导 Ft = mv' – mv0=Δp
即:
合力
末动量
初动量
探究新知
Ft = mv' – mv0=Δp
末动能
初动能
功
末动量
初动量
?
冲量
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I = Ft
3.单位: 牛·秒(N·s)
探究新知
4.意义:
(1)冲量是矢量,作用力的方向不变时其方向与力的方向相同。
(2)冲量是过程量,是力对时间的积累效应。
冲量
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I = FΔt
3.单位: 牛·秒(N·s)
探究新知
t0
F0
F
t
O
I = F0t
探究新知
思考:根据图像求出恒力F0在时间t内的冲量?
若F为变力,如何求其冲量?
将该段时间
无限分割
F
t/s
4
3
2
1
0
2
4
6
10
8
t/s
4
3
2
1
0
2
4
6
10
8
F
t/s
4
3
2
1
0
2
4
6
10
8
F
一段时间内的变力
近似认为物体在每一时段以受到某一恒力
一段时间内的变力的冲量
微分求和
微元法
由图可知F-t图线与时间轴之间所围的“面积”的大小表示对应时间t0内,力F0的冲量的大小。
探究新知
我们可以把碰撞过程细分为很多短暂过程,每个短暂过程中物体所受得力没有很大的变化,这样对于每个短暂过程就能够应用 Ft =Δp ,把应用于每个短暂过程的关系式相加,就得到整个过程的动量定理。在应用Ft =Δp处理变力问题时,式中F应该理解为变力在作用时间内的平均值。
探究新知
4.意义:
(1)冲量是矢量,作用力的方向不变时其方向与力的方向相同。
(2)冲量是过程量,是力对时间的积累效应。
(3)冲量和功不同,恒力在一段时间内可能不作功,但一定有冲量。
(4)冲量的计算要明确求哪个力的冲量,还是物体的合外力的冲量。
I = Ft 只能求恒力的冲量。若合外力是变力,则F 应该理解为变力平均值。
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I = FΔt 3.单位: 牛·秒(N·s)
探究新知
冲量
Ft = mv' – mv0=Δp
动能定理
动量定理
1、内容:物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量。
2、表达式:
探究新知
3、理解:
(1)表明合外力的冲量是动量变化的原因;
(2)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同。
探究新知
(3)动量的变化率:动量的变化跟发生这一变化所用的时间的比值。由动量定理,得 ,可见,动量的变化率等于物体所受的合力。当动量变化较快时,物体所受合力较大,反之较小;当动量均匀变化时,物体所受合力为恒力。
粉笔从某一高度下落,分别与水泥地面和厚布垫接触前的速度是相同的,也即初动量相同,碰撞后速度均变为零,即末动量均为零,因而在相互作用过程中粉笔的动量变化量相同。而两种情况下的相互作用时间不同,与水泥地面碰时作用时间短,与厚布垫相碰时作用时间较长,由 Ft =Δp 知,粉笔与水泥地面相碰时作用大,会被摔断,与厚布相碰时作用力较小,因而不会被摔断。
想一想
让粉笔从相同的高度分别落到水泥地上和铺在地上的厚布上,观察会有怎样的现象发生。
结果:落在水泥地上的粉笔断了,而落在垫有厚布的地上却没有断。
探究新知
举例说明生活中还有那些现象利用了动量定理?
探究新知
动量定理解释生活现象
由Ft=ΔP可知:
①△P一定,t短则F大,t长则F小;
——缓冲装置
②t一定,F大则△P大,F小则△P小;
③F一定,t长则△P大,t短则△P小。
探究新知
一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后,反向水平飞回,速度的大小为45m/s。设球棒与垒球的作用时间t =0.002s,球棒对垒球的平均作用力是多大
分析:球棒对垒球的作用力是变力,力的作用时间很短。在这个短时间内,力先是急剧增大,然后又急剧的减小为0,在冲击、碰撞这类问题中,相互作用的时间很短,力的变化都具有这个特点。动量定理适用于变力作用的过程,因此,可以用动量定理计算棒对垒球的平均作用力。
例题
探究新知
一个质量为0.18kg的垒球,以25m/s 的水平速度飞向球棒,被球棒打击后,反向水平飞回,速度的大小为45m/s。设球棒与垒球的作用时间 t = 0.002 s,球棒对垒球的平均作用力是多大
例题
探究新知
解:沿垒球飞向球棒时的方向建立坐标轴,垒球的初动量为
p=mv=0.18×25kg.m/s=4.5kg.m/s
垒球的末动量为
由动量定理知垒球所受的平均力为
垒球所受的平均作用力的大小为6300N,符号表示力的方向与坐标轴的方向相反,即力的方向与垒球飞来的方向相反。
探究新知
运用动量定理解题的一般步骤
5. 根据动量定理列方程求解。
1. 确定研究对象
2. 对研究对象进行受力分析,确定全部外力及作用时间;
3. 找出物体的初末状态并确定相应的动量;
4. 如果初、末动量在同一直线上,则选定正方向,并给每个力的冲量和初末动量带上正负号,以表示和正方向同向或反向;如果初、末动量不在同一直线上,则用平行四边形定则求解;
探究新知
动量定理的适用范围
1、动量定理不但适用于恒力,也适用于随时间变化的变力,对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
2、动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
3、动量定理不仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
动量定理的优点:不考虑中间过程,只考虑初末状态
探究新知
课堂小结
谢 谢
人教版 / 高中 / 物理
1.2 动量定理
让粉笔从相同的高度分别落到水泥地上和铺在地上的厚布上,观察会有怎样的现象发生。
结果:落在水泥地上的粉笔断了,而落在垫有厚布的地上却没有断。
演示实验:粉笔落地
导入新课
思考:为什么会产生这两种不同的现象?
在前面所学的动能定理中,我们知道,动能的变化是由于力的位移积累即力做功的结果,那么,动量的变化又是什么原因引起的呢?
温故知新
探究新知
汽车以速度V运动,急刹车到停止。若对车施加很大的阻力,则车停止时间很短;如果对车施加很小的阻力,则车停止时间较长。
两种情况下,汽车的_______变化相同。可见,引起运动状态改变,要考虑_______和_________这两个因素。
情境探究
动量
受力
时间
f1
探究新知
问题情景:假设一个质量为m的物体在恒定的合外力F作用下,做匀变速直线运动,初速度为 v,经过一段时间t后,速度变为v′,试探究合外力F的表达式。
理论探究
由牛顿第二定律知:F = ma
加速度:
推导 Ft = mv' – mv0=Δp
即:
合力
末动量
初动量
探究新知
Ft = mv' – mv0=Δp
末动能
初动能
功
末动量
初动量
?
冲量
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I = Ft
3.单位: 牛·秒(N·s)
探究新知
4.意义:
(1)冲量是矢量,作用力的方向不变时其方向与力的方向相同。
(2)冲量是过程量,是力对时间的积累效应。
冲量
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I = FΔt
3.单位: 牛·秒(N·s)
探究新知
t0
F0
F
t
O
I = F0t
探究新知
思考:根据图像求出恒力F0在时间t内的冲量?
若F为变力,如何求其冲量?
将该段时间
无限分割
F
t/s
4
3
2
1
0
2
4
6
10
8
t/s
4
3
2
1
0
2
4
6
10
8
F
t/s
4
3
2
1
0
2
4
6
10
8
F
一段时间内的变力
近似认为物体在每一时段以受到某一恒力
一段时间内的变力的冲量
微分求和
微元法
由图可知F-t图线与时间轴之间所围的“面积”的大小表示对应时间t0内,力F0的冲量的大小。
探究新知
我们可以把碰撞过程细分为很多短暂过程,每个短暂过程中物体所受得力没有很大的变化,这样对于每个短暂过程就能够应用 Ft =Δp ,把应用于每个短暂过程的关系式相加,就得到整个过程的动量定理。在应用Ft =Δp处理变力问题时,式中F应该理解为变力在作用时间内的平均值。
探究新知
4.意义:
(1)冲量是矢量,作用力的方向不变时其方向与力的方向相同。
(2)冲量是过程量,是力对时间的积累效应。
(3)冲量和功不同,恒力在一段时间内可能不作功,但一定有冲量。
(4)冲量的计算要明确求哪个力的冲量,还是物体的合外力的冲量。
I = Ft 只能求恒力的冲量。若合外力是变力,则F 应该理解为变力平均值。
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I = FΔt 3.单位: 牛·秒(N·s)
探究新知
冲量
Ft = mv' – mv0=Δp
动能定理
动量定理
1、内容:物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量。
2、表达式:
探究新知
3、理解:
(1)表明合外力的冲量是动量变化的原因;
(2)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同。
探究新知
(3)动量的变化率:动量的变化跟发生这一变化所用的时间的比值。由动量定理,得 ,可见,动量的变化率等于物体所受的合力。当动量变化较快时,物体所受合力较大,反之较小;当动量均匀变化时,物体所受合力为恒力。
粉笔从某一高度下落,分别与水泥地面和厚布垫接触前的速度是相同的,也即初动量相同,碰撞后速度均变为零,即末动量均为零,因而在相互作用过程中粉笔的动量变化量相同。而两种情况下的相互作用时间不同,与水泥地面碰时作用时间短,与厚布垫相碰时作用时间较长,由 Ft =Δp 知,粉笔与水泥地面相碰时作用大,会被摔断,与厚布相碰时作用力较小,因而不会被摔断。
想一想
让粉笔从相同的高度分别落到水泥地上和铺在地上的厚布上,观察会有怎样的现象发生。
结果:落在水泥地上的粉笔断了,而落在垫有厚布的地上却没有断。
探究新知
举例说明生活中还有那些现象利用了动量定理?
探究新知
动量定理解释生活现象
由Ft=ΔP可知:
①△P一定,t短则F大,t长则F小;
——缓冲装置
②t一定,F大则△P大,F小则△P小;
③F一定,t长则△P大,t短则△P小。
探究新知
一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后,反向水平飞回,速度的大小为45m/s。设球棒与垒球的作用时间t =0.002s,球棒对垒球的平均作用力是多大
分析:球棒对垒球的作用力是变力,力的作用时间很短。在这个短时间内,力先是急剧增大,然后又急剧的减小为0,在冲击、碰撞这类问题中,相互作用的时间很短,力的变化都具有这个特点。动量定理适用于变力作用的过程,因此,可以用动量定理计算棒对垒球的平均作用力。
例题
探究新知
一个质量为0.18kg的垒球,以25m/s 的水平速度飞向球棒,被球棒打击后,反向水平飞回,速度的大小为45m/s。设球棒与垒球的作用时间 t = 0.002 s,球棒对垒球的平均作用力是多大
例题
探究新知
解:沿垒球飞向球棒时的方向建立坐标轴,垒球的初动量为
p=mv=0.18×25kg.m/s=4.5kg.m/s
垒球的末动量为
由动量定理知垒球所受的平均力为
垒球所受的平均作用力的大小为6300N,符号表示力的方向与坐标轴的方向相反,即力的方向与垒球飞来的方向相反。
探究新知
运用动量定理解题的一般步骤
5. 根据动量定理列方程求解。
1. 确定研究对象
2. 对研究对象进行受力分析,确定全部外力及作用时间;
3. 找出物体的初末状态并确定相应的动量;
4. 如果初、末动量在同一直线上,则选定正方向,并给每个力的冲量和初末动量带上正负号,以表示和正方向同向或反向;如果初、末动量不在同一直线上,则用平行四边形定则求解;
探究新知
动量定理的适用范围
1、动量定理不但适用于恒力,也适用于随时间变化的变力,对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
2、动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
3、动量定理不仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
动量定理的优点:不考虑中间过程,只考虑初末状态
探究新知
课堂小结
谢 谢
