2022年高中名校自主招生初升高衔接数学讲义8 几何计算(Word版含答案)
文档属性
| 名称 | 2022年高中名校自主招生初升高衔接数学讲义8 几何计算(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 00:00:00 | ||
图片预览


文档简介
第八讲 几何计算
知识要点
在自招试卷中,有不少的几何计算问题,一般需要用到全等,相似,勾股定理等课本知识,同时也会考查到面积法,弧长等平时较少操练的章节.
本讲我们讲围绕几何计算展开学习.
例题精讲
1. 如图8-1,,点P、Q分别是边OA、OB上的两点,且.将沿PQ折叠,点O落在平面内点C处.
(1)①当时, ;
②当时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
2. 我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
(2)如图8-6,中,,点D在AC上,且,求证:BD是的“内似线”;
(3)如图8-7,在中,,,,点E、F分别在边AC、BC上,且EF是的“内似线”,求EF的长.
3. 将一个等腰三角形ABC划分成两个较小的等腰三角形,问这样的有几种形状?并将所有形状都列出来.
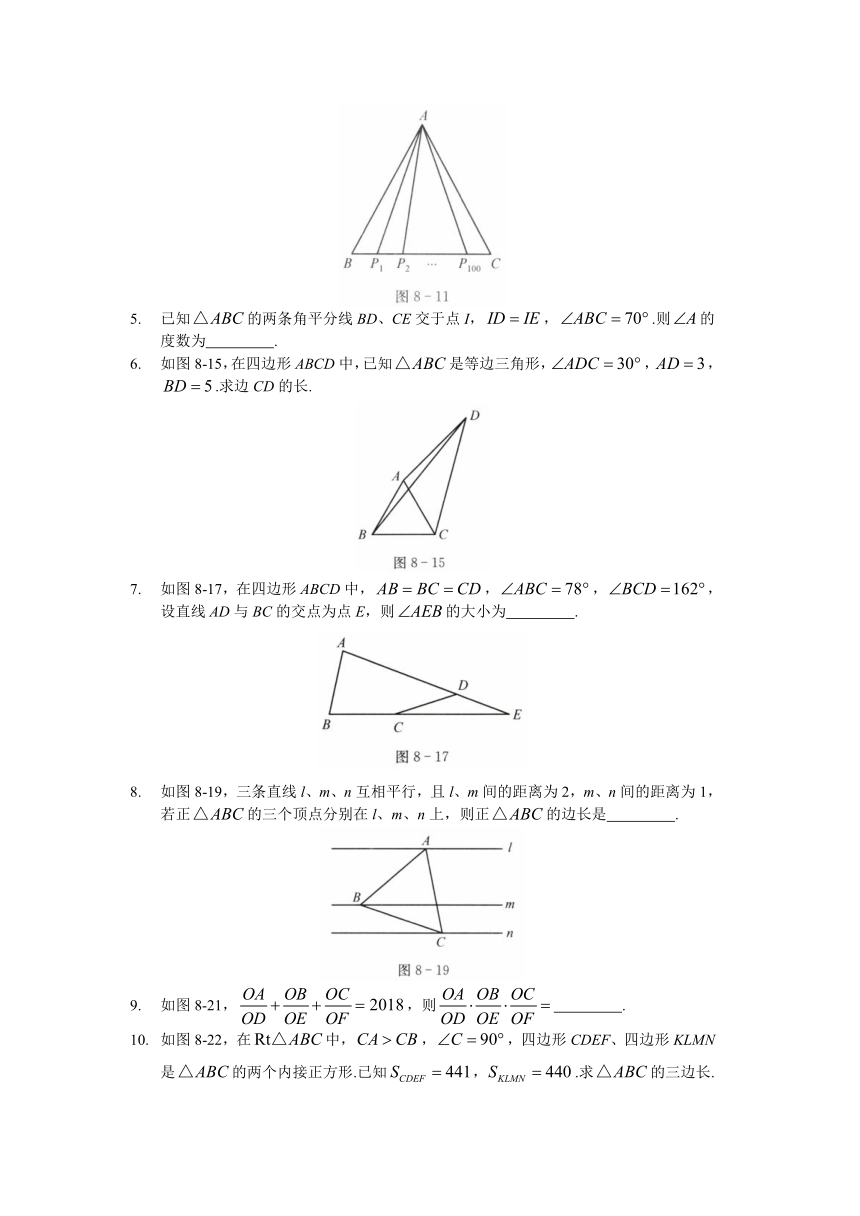
4. 如图8-11,中,,BC边上有100个不同的点,,,…,,记,求.
5. 已知的两条角平分线BD、CE交于点I,,.则的度数为 .
6. 如图8-15,在四边形ABCD中,已知是等边三角形,,,.求边CD的长.
7. 如图8-17,在四边形ABCD中,,,,设直线AD与BC的交点为点E,则的大小为 .
8. 如图8-19,三条直线l、m、n互相平行,且l、m间的距离为2,m、n间的距离为1,若正的三个顶点分别在l、m、n上,则正的边长是 .
9. 如图8-21,,则 .
10. 如图8-22,在中,,,四边形CDEF、四边形KLMN是的两个内接正方形.已知,.求的三边长.
习题巩固
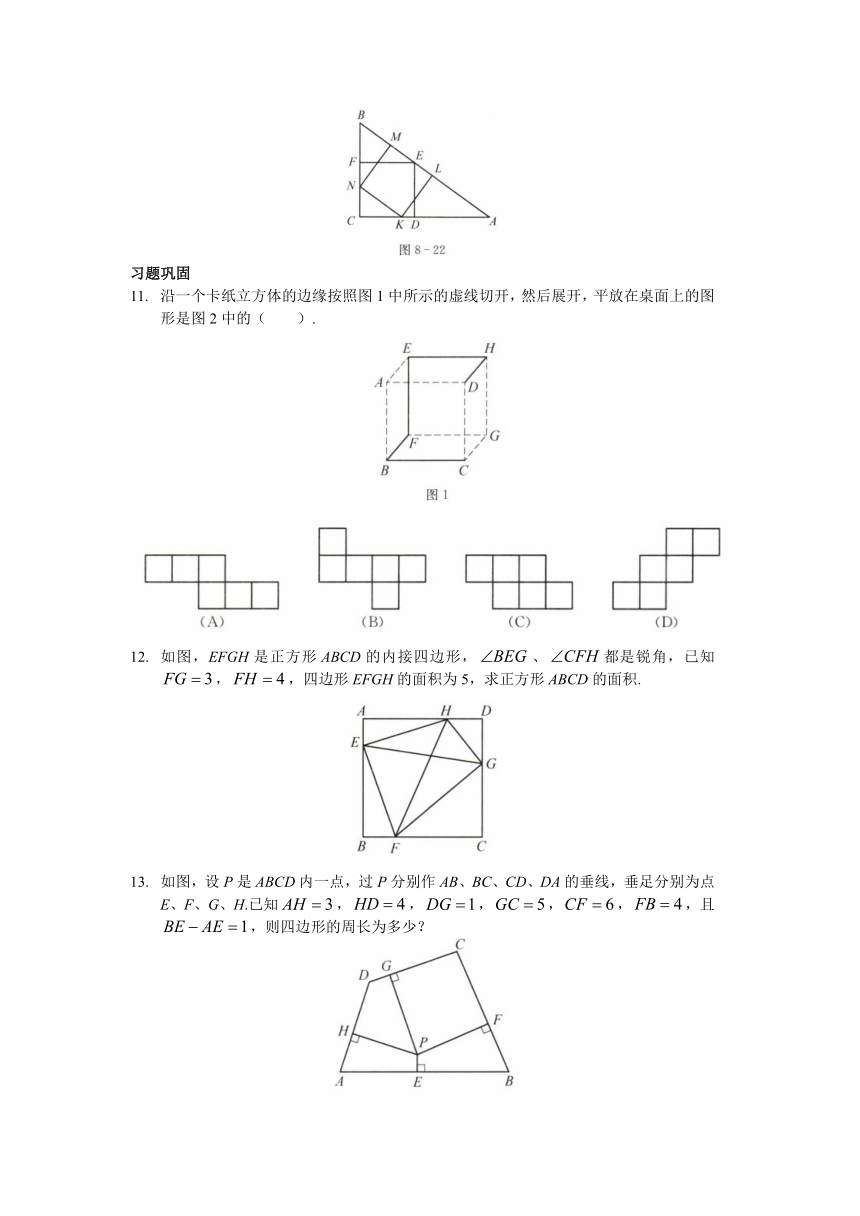
11. 沿一个卡纸立方体的边缘按照图1中所示的虚线切开,然后展开,平放在桌面上的图形是图2中的( ).
12. 如图,EFGH是正方形ABCD的内接四边形,、都是锐角,已知,,四边形EFGH的面积为5,求正方形ABCD的面积.
13. 如图,设P是ABCD内一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为点E、F、G、H.已知,,,,,,且,则四边形的周长为多少?
14. 在中,,,延长BC到D使.求.
15. 已知是等边三角形,它的高是4.若点P到边AB、AC的距离分别是1、2.则点P到边BC的距离是多少?
16. 在中,,,分别以AB、AC为边向外部作正、,连结DE分别交AC、AB于点F、G.则的值为多少?
17. 在中,,,.则外接圆的半径是多少?
18. 设的三边分别为a、b、c,且.若,求的值.
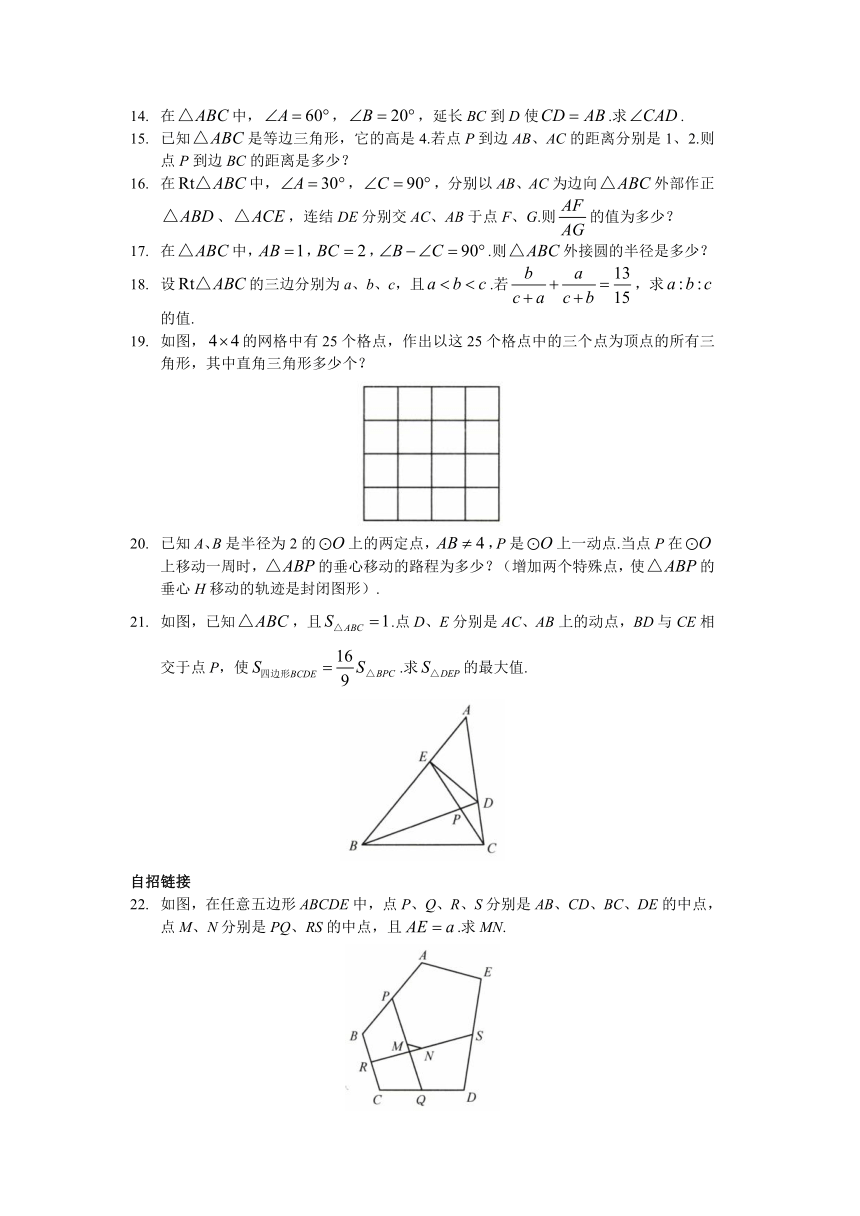
19. 如图,的网格中有25个格点,作出以这25个格点中的三个点为顶点的所有三角形,其中直角三角形多少个?
20. 已知A、B是半径为2的上的两定点,,P是上一动点.当点P在上移动一周时,的垂心移动的路程为多少?(增加两个特殊点,使的垂心H移动的轨迹是封闭图形).
21. 如图,已知,且.点D、E分别是AC、AB上的动点,BD与CE相交于点P,使.求的最大值.
自招链接
22. 如图,在任意五边形ABCDE中,点P、Q、R、S分别是AB、CD、BC、DE的中点,点M、N分别是PQ、RS的中点,且.求MN.
23. 已知中,,于点D,若,.求的面积.
参考答案
1. (1)①当时,,由折叠的性质得:,,所以,所以,所以四边形OPCQ是平行四边形,所以四边形OPCQ是菱形,所以.
故答案为:.
②当时,分两种情况:
(ⅰ)如图8-2所示,设,因为,所以是等腰直角三角形,所以,所以.
由折叠的性质得:,,所以是等腰直角三角形,所以,所以,解得:,即;
(ⅱ)如图8-3所示.同(ⅰ)得:;
综上所述:当时,QQ的长为,或.
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在的内部时,四边形OPCQ是菱形,;
②当点C在的一边上时,是等腰直角三角形,或;
③当点C在的外部时,分两种情况:
(ⅰ)如图8-4所示,,则,由折叠的性质得:.
设,则,在中,由三角形内角和定理得:,解得:,所以,作于点N,设,因为,则,,.
因为,所以,解得:,所以.
(ⅱ)如图8-5所示,,作于点N,同①得:.
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为或或,或或.
2. (1)等边三角形“内似线”的条数为3条;理由如下:
过等边三角形的内心分别作三边的平行线,如8-8所示:则,,,所以MN、EF、GH是等边三角形ABC的“内似线”.故答案为:3.
(2)因为,,所以,,所以.
又因为,所以,所以BD平分,即BD过的内心,所以BD是的“内似线”.
(3)设D是的内心,连结CD,则CD平分,因为EF是的“内似线”,所以与相似.
分两种情况:①当时,,因为,,,所以.
作于点N,如图8-9所示.则,DN是的内切圆半径,所以.
因为CD平分,所以.
因为,所以,所以.
因为,所以,所以,解得:.
②当时,同理得:.
综上所述,EF的长为.
3. 如图8-10所示.设等腰三角形ABC分成与.不妨假设;于是,等腰三角形ABD中,只能有.这时,而有三种情况.
(1)若时,则,为等腰直角三角形.
(2)若时,设,则,,,由于,则.
若,则,;
若,则,.
(3)若时,设,,,显然.
由,得,.
综上所述,总共有4组解;所求三角形的三个内角分别为(45°,45°,90°)、(36°,36°,108°)、,(36°,72°,72°).
4. 仔细观察,我们发现的结构与斯德瓦尔特定理非常相似,只是缺BC.从而可知,
,
故,从而有.也可以仿效前面几个例题作垂线,也可求出.
如图8-12,作于点D,则
.
从而可知,.
5. 答案:40°或60°.
如图8-13,在BC上截取,,连结、.
当点与不重合时,易证,.
则.
故.
又,则,.
当点与重合时,如图8-14.
同理,由,且,知.
所以,.
6. 如图8-16,以CD为边向四边形ABCD外作等边,连结AE.
由,,知
,所以,所以.
又,可知.
所以
,
从而有
,
所以
.
7. 如图8-18,过点B作,过点D作,BF、DF交于点F,连结AF.
因为,,,所以四边形BCDF是菱形,所以.
因为,所以.
因为,所以.
因为,所以.
因为,所以.
所以三角形ABF是等边三角形.
所以,,所以.
因为四边形BCDF是菱形,,所以,所以.
因为,,所以.
因为,所以,所以.
8. 如图8-20,过点A作于点D,在AD右侧作,并使,连结CE,交l于点F;过点C作于点G.
因为,,所以.
所以,即
因为所以,所以.
因为,所以,所以,所以.
因为,,所以,所以.
因为,所以.
因为,,所以,.
所以,所以
在中,,,所以.
在中,,,所以.
所以.
所以,即正三角形ABC的边长是.
9. 设,,,.则
,
,
;
所以
.
10. 设正方形CDEF的边长为x,正方形KLMN的边长为y,则,.
设,,,则.
因为,所以.
因为,得.
因为,得.
因为,所以.
则
.
所以.
所以,.
所以a、b是二次方程的两根.
因为,所以,.
习题巩固
11. 答案:D.
如图,在立方体的六个面中,只有ABCD和CDHG切开三条棱,保留一条棱连结,即只与一个面相连结,其他四个面切开两条棱,保留两条棱连结,即可与两个面相连结,连结顺序是
.
12. 如图,分别过点E、F、G、H作对边的垂线,得矩形PQRT.
设正方形ABCD的边长为x,,.由勾股定理,得,.
又,,,,且,所以,得
,解得,所以,即.
13. 如图,分别连结PA、PB、PC、PD.因为,,,,所以由勾股定理,得
,
,
,
,
以上四式相加并整理,得
,
因为,,,,,,所以
,
,
因为,所以,所以
.
14. 答案:80°.
如图,在边CD上取点E,使,连结AE.则
.
故.易知.所以,.
15. 如图1,设点P在的内部,AH是的高,P到三边的垂线分别为PD、PE、PF,并记的边长为a.
由面积关系得
,
于是,,即.
类似地,当点P不在的内部时,可知在图2中的位置.
因到AB、AC的距离之和小于4,所以,不是P.记到BC的距离分别为.则
,
,
.
解得,,.故点P到边BC的距离可能是1、3、5、7.
16. 如图,过E作于点M,延长EM交AB于点N,连结DN.则M是AC的中点,且.所以,N是AB的中点.于是,.
又,得,,所以,四边形ADNE是平行四边形.因此,
.
令,则,,.
在中,,.
由得,则,即.
所以,,故.
17. 如图,设O是外接圆的圆心,作直径AD,连结DB、DC.则.
由,,则,.
过点C作AD的垂线,垂足为点F.设,.
由勾股定理得
.
代入得
. ①
在中,由勾股定理得,即
. ②
由式①、②得,即.解得(负值舍去).
18. 因为,,所以
.
即.两边平方并整理得
或.
又,且,则.
19. 答案:596.
(1)当直角三角形的两直角边均在网格线上时,每个顶点为直角顶点,该直角顶点处有个直角三角形.此时,共有个直角三角形.
(2)当直角三角形的两直角边不在网格线上时.
如图,其中,(A)表示与A的地位相同的点,(B)、(C)、(D)与之类似.
以四角顶点为直角的直角三角形不存在;
以点A为直角顶点的直角三角形有(个);
以点B为直角顶点的直角三角形有(个);
以点C为直角顶点的直角三角形为(个);
以点D为直角顶点的直角三角形有(个);
以点O为直角顶点的直角三角形有(个).
综上,所求三角形的个数为(个).
20. 答案:.
当点P在优弧AB上,且为锐角三角形时,.当为钝角三角形时,.当为直角三角形时,垂心为A或B.
当点P在劣弧AB上时,.所以,H的轨迹为关于AB的对称圆(增加两个特殊点为A、B两点关于该圆的圆心的对称点).故的垂心H移动的路程为.
21. 设,,则.因为,所以,,在中,由梅涅劳斯定理,得,则
.
同理, .
所以 .
因为,所以,所以
.
因为,所以
,
.
令,则,从而
.
因为,所以,即,当且仅当时,,则
,
所以当且仅当,即时,.
自招链接
22. 如图,连结BE,并取其中点为O,再连结PO、SO、RO、SQ、RQ、OQ.
在中,由三角中位线定理得.
在四边形BCDE中,因R、Q、S、O分别为各边的中点,
易知四边形RQSO为平行四边形,其对角线RS、QO互相平分.
又N为RS的中点,则N也是OQ的中点.故.于是,.
23. 法一:如图1,将沿直线AB翻折得,将沿直线AC翻折得,延长EB、FC交于点G.
因为,所以,,因为,根据平行线间的距离相等,易得.又,.
设.则,,可列方程:
.
解得:(其中不合题意,舍去.)
所以的面积为:.
法二:将绕着点A逆时针旋转90°得,延长、DC交于点H,连结.
因为,所以,,根据平行线间的距离相等,得,且.所以.
设.则,,在中,由勾股定理得
.
解得(其中不合题意,舍去.)
所以的面积为:.
法三:正切和公式:.
设,则,解方程得(其中不合题意,舍去.)所以的面积为:.
知识要点
在自招试卷中,有不少的几何计算问题,一般需要用到全等,相似,勾股定理等课本知识,同时也会考查到面积法,弧长等平时较少操练的章节.
本讲我们讲围绕几何计算展开学习.
例题精讲
1. 如图8-1,,点P、Q分别是边OA、OB上的两点,且.将沿PQ折叠,点O落在平面内点C处.
(1)①当时, ;
②当时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
2. 我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
(2)如图8-6,中,,点D在AC上,且,求证:BD是的“内似线”;
(3)如图8-7,在中,,,,点E、F分别在边AC、BC上,且EF是的“内似线”,求EF的长.
3. 将一个等腰三角形ABC划分成两个较小的等腰三角形,问这样的有几种形状?并将所有形状都列出来.
4. 如图8-11,中,,BC边上有100个不同的点,,,…,,记,求.
5. 已知的两条角平分线BD、CE交于点I,,.则的度数为 .
6. 如图8-15,在四边形ABCD中,已知是等边三角形,,,.求边CD的长.
7. 如图8-17,在四边形ABCD中,,,,设直线AD与BC的交点为点E,则的大小为 .
8. 如图8-19,三条直线l、m、n互相平行,且l、m间的距离为2,m、n间的距离为1,若正的三个顶点分别在l、m、n上,则正的边长是 .
9. 如图8-21,,则 .
10. 如图8-22,在中,,,四边形CDEF、四边形KLMN是的两个内接正方形.已知,.求的三边长.
习题巩固
11. 沿一个卡纸立方体的边缘按照图1中所示的虚线切开,然后展开,平放在桌面上的图形是图2中的( ).
12. 如图,EFGH是正方形ABCD的内接四边形,、都是锐角,已知,,四边形EFGH的面积为5,求正方形ABCD的面积.
13. 如图,设P是ABCD内一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为点E、F、G、H.已知,,,,,,且,则四边形的周长为多少?
14. 在中,,,延长BC到D使.求.
15. 已知是等边三角形,它的高是4.若点P到边AB、AC的距离分别是1、2.则点P到边BC的距离是多少?
16. 在中,,,分别以AB、AC为边向外部作正、,连结DE分别交AC、AB于点F、G.则的值为多少?
17. 在中,,,.则外接圆的半径是多少?
18. 设的三边分别为a、b、c,且.若,求的值.
19. 如图,的网格中有25个格点,作出以这25个格点中的三个点为顶点的所有三角形,其中直角三角形多少个?
20. 已知A、B是半径为2的上的两定点,,P是上一动点.当点P在上移动一周时,的垂心移动的路程为多少?(增加两个特殊点,使的垂心H移动的轨迹是封闭图形).
21. 如图,已知,且.点D、E分别是AC、AB上的动点,BD与CE相交于点P,使.求的最大值.
自招链接
22. 如图,在任意五边形ABCDE中,点P、Q、R、S分别是AB、CD、BC、DE的中点,点M、N分别是PQ、RS的中点,且.求MN.
23. 已知中,,于点D,若,.求的面积.
参考答案
1. (1)①当时,,由折叠的性质得:,,所以,所以,所以四边形OPCQ是平行四边形,所以四边形OPCQ是菱形,所以.
故答案为:.
②当时,分两种情况:
(ⅰ)如图8-2所示,设,因为,所以是等腰直角三角形,所以,所以.
由折叠的性质得:,,所以是等腰直角三角形,所以,所以,解得:,即;
(ⅱ)如图8-3所示.同(ⅰ)得:;
综上所述:当时,QQ的长为,或.
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在的内部时,四边形OPCQ是菱形,;
②当点C在的一边上时,是等腰直角三角形,或;
③当点C在的外部时,分两种情况:
(ⅰ)如图8-4所示,,则,由折叠的性质得:.
设,则,在中,由三角形内角和定理得:,解得:,所以,作于点N,设,因为,则,,.
因为,所以,解得:,所以.
(ⅱ)如图8-5所示,,作于点N,同①得:.
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为或或,或或.
2. (1)等边三角形“内似线”的条数为3条;理由如下:
过等边三角形的内心分别作三边的平行线,如8-8所示:则,,,所以MN、EF、GH是等边三角形ABC的“内似线”.故答案为:3.
(2)因为,,所以,,所以.
又因为,所以,所以BD平分,即BD过的内心,所以BD是的“内似线”.
(3)设D是的内心,连结CD,则CD平分,因为EF是的“内似线”,所以与相似.
分两种情况:①当时,,因为,,,所以.
作于点N,如图8-9所示.则,DN是的内切圆半径,所以.
因为CD平分,所以.
因为,所以,所以.
因为,所以,所以,解得:.
②当时,同理得:.
综上所述,EF的长为.
3. 如图8-10所示.设等腰三角形ABC分成与.不妨假设;于是,等腰三角形ABD中,只能有.这时,而有三种情况.
(1)若时,则,为等腰直角三角形.
(2)若时,设,则,,,由于,则.
若,则,;
若,则,.
(3)若时,设,,,显然.
由,得,.
综上所述,总共有4组解;所求三角形的三个内角分别为(45°,45°,90°)、(36°,36°,108°)、,(36°,72°,72°).
4. 仔细观察,我们发现的结构与斯德瓦尔特定理非常相似,只是缺BC.从而可知,
,
故,从而有.也可以仿效前面几个例题作垂线,也可求出.
如图8-12,作于点D,则
.
从而可知,.
5. 答案:40°或60°.
如图8-13,在BC上截取,,连结、.
当点与不重合时,易证,.
则.
故.
又,则,.
当点与重合时,如图8-14.
同理,由,且,知.
所以,.
6. 如图8-16,以CD为边向四边形ABCD外作等边,连结AE.
由,,知
,所以,所以.
又,可知.
所以
,
从而有
,
所以
.
7. 如图8-18,过点B作,过点D作,BF、DF交于点F,连结AF.
因为,,,所以四边形BCDF是菱形,所以.
因为,所以.
因为,所以.
因为,所以.
因为,所以.
所以三角形ABF是等边三角形.
所以,,所以.
因为四边形BCDF是菱形,,所以,所以.
因为,,所以.
因为,所以,所以.
8. 如图8-20,过点A作于点D,在AD右侧作,并使,连结CE,交l于点F;过点C作于点G.
因为,,所以.
所以,即
因为所以,所以.
因为,所以,所以,所以.
因为,,所以,所以.
因为,所以.
因为,,所以,.
所以,所以
在中,,,所以.
在中,,,所以.
所以.
所以,即正三角形ABC的边长是.
9. 设,,,.则
,
,
;
所以
.
10. 设正方形CDEF的边长为x,正方形KLMN的边长为y,则,.
设,,,则.
因为,所以.
因为,得.
因为,得.
因为,所以.
则
.
所以.
所以,.
所以a、b是二次方程的两根.
因为,所以,.
习题巩固
11. 答案:D.
如图,在立方体的六个面中,只有ABCD和CDHG切开三条棱,保留一条棱连结,即只与一个面相连结,其他四个面切开两条棱,保留两条棱连结,即可与两个面相连结,连结顺序是
.
12. 如图,分别过点E、F、G、H作对边的垂线,得矩形PQRT.
设正方形ABCD的边长为x,,.由勾股定理,得,.
又,,,,且,所以,得
,解得,所以,即.
13. 如图,分别连结PA、PB、PC、PD.因为,,,,所以由勾股定理,得
,
,
,
,
以上四式相加并整理,得
,
因为,,,,,,所以
,
,
因为,所以,所以
.
14. 答案:80°.
如图,在边CD上取点E,使,连结AE.则
.
故.易知.所以,.
15. 如图1,设点P在的内部,AH是的高,P到三边的垂线分别为PD、PE、PF,并记的边长为a.
由面积关系得
,
于是,,即.
类似地,当点P不在的内部时,可知在图2中的位置.
因到AB、AC的距离之和小于4,所以,不是P.记到BC的距离分别为.则
,
,
.
解得,,.故点P到边BC的距离可能是1、3、5、7.
16. 如图,过E作于点M,延长EM交AB于点N,连结DN.则M是AC的中点,且.所以,N是AB的中点.于是,.
又,得,,所以,四边形ADNE是平行四边形.因此,
.
令,则,,.
在中,,.
由得,则,即.
所以,,故.
17. 如图,设O是外接圆的圆心,作直径AD,连结DB、DC.则.
由,,则,.
过点C作AD的垂线,垂足为点F.设,.
由勾股定理得
.
代入得
. ①
在中,由勾股定理得,即
. ②
由式①、②得,即.解得(负值舍去).
18. 因为,,所以
.
即.两边平方并整理得
或.
又,且,则.
19. 答案:596.
(1)当直角三角形的两直角边均在网格线上时,每个顶点为直角顶点,该直角顶点处有个直角三角形.此时,共有个直角三角形.
(2)当直角三角形的两直角边不在网格线上时.
如图,其中,(A)表示与A的地位相同的点,(B)、(C)、(D)与之类似.
以四角顶点为直角的直角三角形不存在;
以点A为直角顶点的直角三角形有(个);
以点B为直角顶点的直角三角形有(个);
以点C为直角顶点的直角三角形为(个);
以点D为直角顶点的直角三角形有(个);
以点O为直角顶点的直角三角形有(个).
综上,所求三角形的个数为(个).
20. 答案:.
当点P在优弧AB上,且为锐角三角形时,.当为钝角三角形时,.当为直角三角形时,垂心为A或B.
当点P在劣弧AB上时,.所以,H的轨迹为关于AB的对称圆(增加两个特殊点为A、B两点关于该圆的圆心的对称点).故的垂心H移动的路程为.
21. 设,,则.因为,所以,,在中,由梅涅劳斯定理,得,则
.
同理, .
所以 .
因为,所以,所以
.
因为,所以
,
.
令,则,从而
.
因为,所以,即,当且仅当时,,则
,
所以当且仅当,即时,.
自招链接
22. 如图,连结BE,并取其中点为O,再连结PO、SO、RO、SQ、RQ、OQ.
在中,由三角中位线定理得.
在四边形BCDE中,因R、Q、S、O分别为各边的中点,
易知四边形RQSO为平行四边形,其对角线RS、QO互相平分.
又N为RS的中点,则N也是OQ的中点.故.于是,.
23. 法一:如图1,将沿直线AB翻折得,将沿直线AC翻折得,延长EB、FC交于点G.
因为,所以,,因为,根据平行线间的距离相等,易得.又,.
设.则,,可列方程:
.
解得:(其中不合题意,舍去.)
所以的面积为:.
法二:将绕着点A逆时针旋转90°得,延长、DC交于点H,连结.
因为,所以,,根据平行线间的距离相等,得,且.所以.
设.则,,在中,由勾股定理得
.
解得(其中不合题意,舍去.)
所以的面积为:.
法三:正切和公式:.
设,则,解方程得(其中不合题意,舍去.)所以的面积为:.
同课章节目录
