2022年高中名校自主招生初升高衔接数学讲义11 组合(Word版含答案)
文档属性
| 名称 | 2022年高中名校自主招生初升高衔接数学讲义11 组合(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 00:00:00 | ||
图片预览




文档简介
第十一讲 组合
知识要点
组合问题非常考验同学们的思维能力,其中组合计数、概率等问题是自招考试的高频考点,抽屉原理、染色问题、极端原理等偶尔也会出现.
一、乘法原理
一般地,如果完成一件事需要n个步骤(缺一不可),第1步有m1种不同的方法,第2步有m2种不同的方法,第3步有m3种不同的方法……第n步有mn种不同的方法,则完成这件事一共有种不同的方法.
乘法原理运用的范围:这件事要分几个彼此互不影响的独立步骤来完成,这几步是完成这件任务缺一不可,这样的问题可以使用乘法原理解决.我们可以简记为:“乘法分步,步步相关”.
二、加法原理
一般地,如果完成一件事有n类步骤(每一类中的任何一种方法都能独立完成这件事情),第1类有m1,种不同的方法,第2类有m2种不同的方法,第3类有m3种不同的方法……第n类有mn种不同的方法,则完成这件事一共有种不同的方法.
加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.
三、排列
在实际生活中经常会遇到这样的问题,就是要把一些事物排在一起,构成一列,计算有多少种排法,就是排列问题.在排的过程中,不仅与参与排列的事物有关,而且与各事物所在的先后顺序有关.
根据排列的定义,两个排列相同,指的是两个排列的元素完全相同,并且元素的排列顺序也相同.如果两个排列中,元素不完全相同,它们是不同的排列;如果两个排列中,虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.
排列的基本问题是计算排列的总个数.
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素的排列中取出m个元素的排列数,我们把它记做或.
.
四、组合
一般地,从n个不同元素中取出m个(m≤n)元素组成一组不计较组内各元素的次序,叫做从n个不同元素中取出m个元素的一个组合.
从排列和组合的定义可以知道,排列与元素的顺序有关,而组合与顺序无关.如果两个组合中的元素完全相同,那么不管元素的顺序如何,都是相同的组合,只有当两个组合中的元素不完全相同时.才是不同的组合.
从n个不同元素中取出m个元素(m≤n)的所有组合的个数,叫做从n个不同元素中取出m个不同元素的组合数.记作或.
例题精讲
1. 回答下列问题:
(1)在1~5的自然数可以组成的五位数共有几个?
(2)有3种染料给三行144列的方格网染色,一共有多少种染色方法(只列式,不计算)?至少取多少列方格,才能保证有两列方格染色完全相同?
(3)从十位同学中任意选取2名同学,一共有多少种选法?
(4)爸爸、妈妈、客人和我四人围着圆桌喝茶.若只考虑每人左邻的情况,问共有多少种不同的入座方法?
(5)图11-l中有六个点,任意三个点都不在一条直线上.请问:以这些点为顶点,一共可以连出多少个三角形?
(6)某铁路线上,在起点和终点之间原有7个车站,现在新增加了3个车站,这样需要增加几种不同的车票?
2. 6人同时被邀请参加一项活动.必须有人去,去几个人自行决定,共有多少种不同的去法?
3. 小明的妈妈给了小明9块一样的糖,让他在接下来的4天正好吃完,每天至少吃一块,则小明有多少种不同的吃糖方案?
4. 4个人进行篮球训练,互相传球接球,要求每个人接球后马上传给别人,开始由甲发球,并作为第一次传球,第五次传球后,球又回到甲手中,问有多少种传球方法?
5. 游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?
6. 给定一个15×15的方格表,将其中有公共边的方格称为相邻的.将某些相邻方格的中心用线段相连,得到一条不白交的闭折线.现知该折线关于方格表的一条对角线对称.证明:折线的长度不大于200.
7. 物体A和B放在坐标平面上同时移动,且每次移动一个单位长度,A从(0,0)开始移动每次以相同的可能性向右或向上移动,物体B从(5,7)开始移动,每次以相同的可能性向左或向下移动,问两物体相遇的可能性是多少?
8. 摄影师给8名同学照相,有两人合影,也有三人合影,若任意两名同学都恰好合影一次,问最少要拍多少张照片?
9. 某同学在暑假里做数学竞赛题,每天至少做一题,每星期至多做12题,一共做了7个星期,求证:该同学在连续的若干天里恰好做了12道题.
10. 平面上有20个点,在他们之间已连了n线段,若任意三点之间都至少有一条线段.求n的最小值.
11. 20个红球、17个白球,重量都是正整数.红球与白球重量之和相等,且都小于340.证明:一定可以取出一些红球和一些白球,使得这些红球重量之和等于这些白球重量之和(不能全取).
习题巩固
12. 某件工作需要钳工2人和电工2人共同完成.现有钳工3人、电工3人,另有1人钳工、电工都会.从7人中挑选4人完成这项工作,共有多少种方法?
13. 平面上10个两两相交的圆最多能将平面分割成多少个区域?
14. 在图中(单位:厘米):
(1)一共有几个长方形?
(2)所有这些长方形面积的和是多少?
15. 有11名外语翻译人员,其中5名是英语翻译员,4名是日语翻译员,另外两名英语、日语都精通.从中找出8人,使他们组成两个翻译小组,其中4人翻译英文,另4人翻译日文,这两个小组能同时工作.问这样的分配名单共可以开出多少张?
16. 假如电子计时器所显示的十个数字是“0126093028”这样一串数,它表示的是1月26日9时30分28秒.在这串数里,“0”出现了3次,“2”出现了2次,“1”、“3”、“6”、“8”、“9”各出现1次,而“4”、“5”、“7”没有出现.如果在电子计时器所显示的这串数里.“0”、“1”、“2”、“3”、“4”、“5”、“6”、“7”、“8”、“9”这十个数字都只出现一次,称它所表示的时刻为“十全时”.那么2016年一共有几个这样的“十全时”?
17. 从1,2,…,2011中选取n个数,使得其中任意两数的差都不等于4或7.求n的最大值.
18. 7名学生参加演出,学校为他们安排了m次演出,每次由其中3名同学同时登台演出,请你设计一种方案,使得7名学生中,任意两名同台演出的次数一样多,且使m最小.
19. 求证:任意9个整数中,必有5个整数,它们的和被5整除.
20. 有红、黄、蓝卡片各6张,分别写有数字1、2、3、4、5、6.从中选取6张,要求三色俱全,且数字1、2、3、4、5、6各一张,则不同的选法有多少种?
自招链接
21. 在右图中,不包含☆的长方形有 个.
22. 第二季“中国好声音”杨坤组某一学员和那英组某一学员进行一对一PK,9位专业评委依次给两位学员投票,最终杨坤组学员拿到5票,那英组学员拿到4票.请问在依次投票的过程中,杨坤组学员得票数一直严格大于那英组学员得票数的概率是多少?
参考答案
1. (1)根据乘法原理,5×5×5×5×5=3125.共有3125个.
(2)根据乘法原理,.
抽屉原理,从最坏的情况考虑取到的第一个是列.
(3).
(4)4个相异元素的环形排列问题,共有种不同的入座方法.
(5)因为任意三个点都不在一条直线上;
所以以这些点为顶点,一共可以连出个三角形.
(6)原来有车站7+2=9,现在有车站9+3=12.
考虑每两个站点之间的往返车票起始站和终点站互异,所以新增的车票种类为
种.
2. (法一)可以分为一人去、两人去、三人去、四人去、五人去、六人去六种情况,每种情况都是组合问题.
第一种情况有6种去法;
第二种情况有种去法;
第三种情况有种去法;
第四种情况有种去法;
第五种情况有种去法;
第六种情况有种去法.
根据加法原理,共有6+15+20+15+6+1=63种不同的去法.
(法二)每个人都有去或不去两种可能,因此共有26种可能,但必须有人去,即所有人都不去的情况必须排除,因此有种.
3. 插板法:9块一样的糖有8个间隔,要分成4份,需要3个问隔,所以有种方案.
4. 设第n次传球后,球又回到甲手中的传球方法有an种.可以想象前次传球,如果每一次传球都任选其他三人中的一人进行传球,即每次传球都有3种可能,由乘法原理,共有(种)传球方法.这些传球方法并不是都符合要求的,它们可以分为两类,一类是第次恰好传到甲手中,这有种传法,它们不符合要求,因为这样第n次无法再把球传给甲;另一类是第次传球,球不在甲手中,第n次持球人再将球传给甲,有an种传法.根据加法原理,有.
由于甲是发球者,一次传球后球又回到甲手中的传球方法是不存在的,所以.
利用递推关系可以得到:,,,.
这说明经过5次传球后,球仍回到甲手中的传球方法有60种.
本题也可以列表求解.
由于第n次传球后,球不在甲手中的传球方法,第n+1次传球后球就可能回到甲手中,所以只需求出第四次传球后,球不在甲手中的传法共有多少种.
第n次传球 传球的方法 球在甲手中的传球方法 球不在甲手中的传球方法
1 3 0 3
2 9 3 6
3 27 6 21
4 81 21 60
5 243 60 183
从表中可以看出经过五次传球后,球仍回到甲手中的传球方法共有60种.
5. 与类似题目找对应关系.
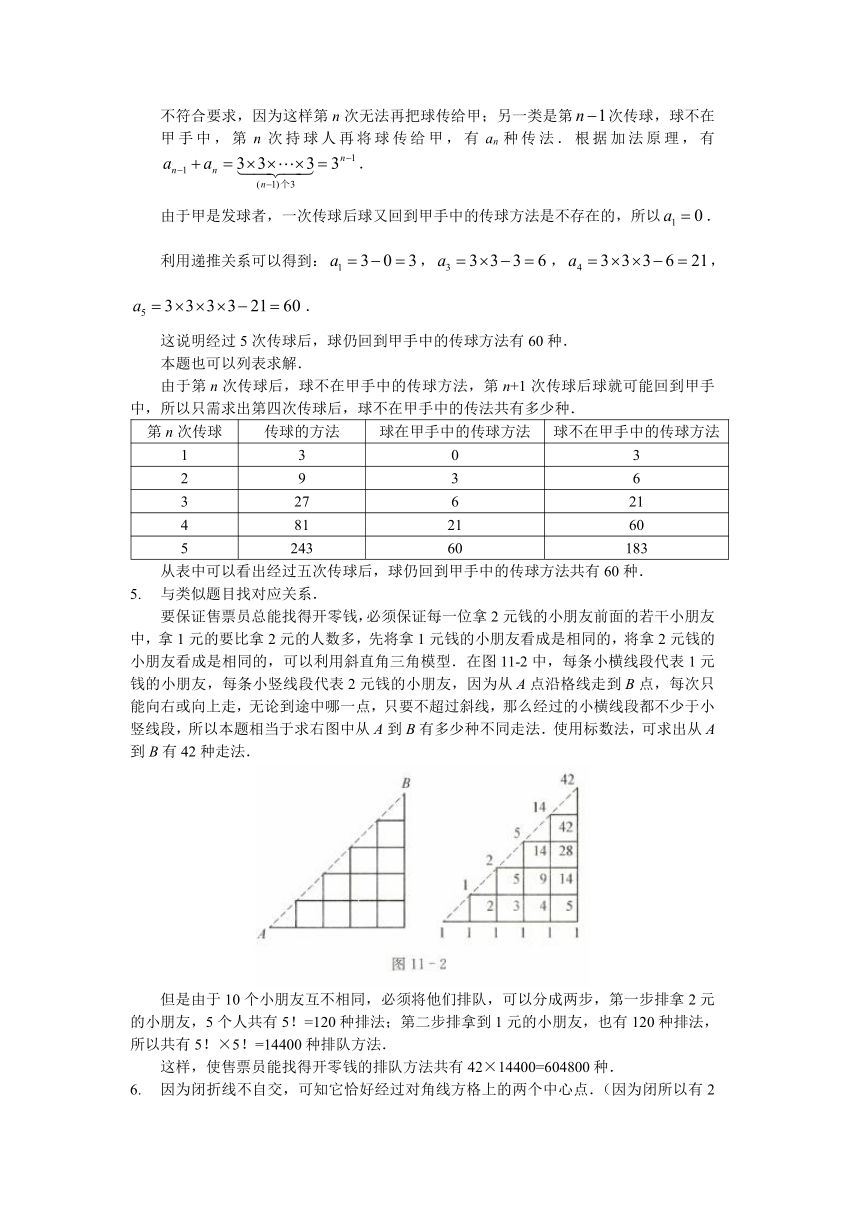
要保证售票员总能找得开零钱,必须保证每一位拿2元钱的小朋友前面的若干小朋友中,拿1元的要比拿2元的人数多,先将拿1元钱的小朋友看成是相同的,将拿2元钱的小朋友看成是相同的,可以利用斜直角三角模型.在图11-2中,每条小横线段代表1元钱的小朋友,每条小竖线段代表2元钱的小朋友,因为从A点沿格线走到B点,每次只能向右或向上走,无论到途中哪一点,只要不超过斜线,那么经过的小横线段都不少于小竖线段,所以本题相当于求右图中从A到B有多少种不同走法.使用标数法,可求出从A到B有42种走法.
但是由于10个小朋友互不相同,必须将他们排队,可以分成两步,第一步排拿2元的小朋友,5个人共有5!=120种排法;第二步排拿到1元的小朋友,也有120种排法,所以共有5!×5!=14400种排队方法.
这样,使售票员能找得开零钱的排队方法共有42×14400=604800种.
6. 因为闭折线不自交,可知它恰好经过对角线方格上的两个中心点.(因为闭所以有2个,因为不自交所以只能为2个.)那么可以得到这条闭折现一定不经过其他的13个对角线方格的中心点.将15×15的方格表黑白二染色,对角线染黑色,则黑色小方格一定比白色小方格多一个.又因为折线上的中心点所在的小方格是黑白交替出现的,所以闭折曲线上的黑点和白点个数是相等的.如果闭折线不经过13个黑点,那么他必然不经过12个白点.所以闭折线经过的中心点的个数最多不超过;也就是说,折线的长度不大于200.
7. 因为从A到B的距离为12,所以要移动6次,物体A和B才能相遇.
在6次移动中,不同的移动方式有种.
其中A和B能相遇的移动方式有
.
故A和B相遇的可能性为.
8. 设3人合影的有x张,两人合影的有y张,则
.
因为每两人都恰好合影一张,所以每人至多可拍3张合影.故等则x≤8,所以
.
将8人编号为1,2,3,4,5,6,7,8;
8张三人合影为:(1,2,4),(2,3,5),(3,4,6),(4,5,7),(5,6,8),(6,7,9),(7,8,2),(8,1,3);
4张二人合影为:(1,5),(2,6),(3,7),(4,8);
显然这12张照片满足条件,所以最少要拍12张.
9. 设前n天做了an;那么
,
.
上面这98个数不同的取值最多96种.所以其中必有两数相等.
不妨设,则.
这表明从第(i+1)天开始,到第j天这连续若干天里恰好做了12道题.
10. 设A点连出的线段数最少,且为k条(0≤k≤19);将20个点分为两组,一组为A点和所有与A相连的k个点,共(k+1)个点;另外一组为余下的点,为是个点;对于第一组的(k+1)个点,因为A点连出的最少为k,所以他们连出的最少为;对于第二组的是个点,他们都不和A点相连,那么如果选取A点和他们其中的两个点,那么这三点之间至少有一条直线,于是第二组的是个点必须两两相连,共有条线.两者相加最少为.所以.
整理得:当且仅当k=9时取“=”.
下面构造一种方法证明90是可以的:20个点分为2组,每组10个点.同组的两两相连,不同组的不连.共连满足题意;
综上:n的最小值为90.
11. 对20个红球、17个白球的重量做排序,,记,由已知条件知.
考虑共340个元素,由抽屉原理,它们模339必有两个是同余的,不妨设
,
那么.
又因为,,所以,也就是得到了
,
命题得证.
习题巩固
12. 分两类情况讨论:
(1)都会的这1人被挑选中,则有:
①如果这人做钳工的话,则再按乘法原理,先选一名钳工有3种方法,再选2名电工也有3种方法,所以有33=9种方法.
②同样,这人做电工,也有9种方法.
(2)都会的这一人没有被挑选,则从3名钳工中选2人,有3种方法,从3名电工中选2人,也有3种方法,一共有33=9种方法.
所以,根据加法原理,一共有9+9+9=27种方法.
13. 先考虑最简单的情形,为了叙述方便,设平面上k个圆最多能将平面分割成ak个部分.
从图1中可以看出,,,,,…
可以发现ak满足下列关系式:.
实际上,当平面上的个圆把平面分成个区域时,如果再在平面上出现第k个圆,为了保证划分平面的区域尽可能多,新添的第k个圆不能通过平面上前个圆之间的交点.这样,第k个圆与前面个圆共产生个交点,如图2:
这个交点把第k个圆分成了段圆弧,而这段圆弧中的每一段都将所在的区域一分为二,所以也就是整个平面的区域数增加了个部分.所以,.
那么,
故10个圆最多能将平面分成92部分.
14. (1)一共有(个)长方形;
(2)所求的和是
(平方厘米).
15. 针对两名英语、日语都精通人员(以下称多面手)的参与情况分成三类:
(1)多面手不参加,则需从5名英语翻译员中选出4人,有种选择,需从4名日语翻译员中选出4人,有1种选择.由乘法原理,有种选择.
(2)多面手中有一人参加,有2种选择,而选出的这个人又有参加英文或日文翻译两种可能:
①如果参加英文翻译,则需从5名英语翻译员中再选出3人,有选择,需从4名日语翻译员中选出4人,有1种选择,由乘法原理,有种选择;
②如果参加日文翻译,则需从5名英语翻译员中选出4人,有种选择,需从4名日语翻译员中再选出3名,有种选择,由乘法原理,有种选择.
根据加法原理,多面手中有一人参加,有种选择.
(3)多面手中两人均参加,有一种选择,但此时又分三种情况:
①两人都译英文,②两人都译日文,③两人各译一个语种.
情况①中,还需从5名英语翻译员中选出2人,有种选择,需从4名日语翻译员中选4人,有1种选择.由乘法原理,有种选择.
情况②中,需从5名英语翻译员中选出4人,有种选择,还需从4名日语翻译员中选出2人,有种选择.
根据乘法原理,共有种选择.
情况③中,两人各译一个语种,有两种安排即两种选择,剩下的需从5名英语翻译员中选出3人,有种选择,需从4名日语翻译员中选出3名,有种选择,由乘法原理,有种选择.
根据加法原理,多面手中两人均参加,一共有种选择.
综上所述,由加法原理,这样的分配名单共可以开出张.
16. (1)容易验证在1、2、10、11、12月内没有“十全时”
(2)3月里只有形式032 1 □ □ 符合条件,其中2个方格中可以填4或5,4条横线上可以填6或7或8或9,所以3月里有个“十全时”.
同理,4、5月里各有48个“十全时”.
(3)6月里有2种形式:①061 23□ □ ,②062 1 □ □ .
①061 23□ □ 中,2个方格中可以填4或5,3条横线上可以填7或8或9,
②062 1 □ □ 中,2个方格中可以填3或4或5,4条横线上可以填7或8或9或3、4、5中余下的某一个.
所以6月里有个“十全时”.
同理,7、8、9月里各有156个“十全时”.
综上所述,2016年一共有个这样的“十全时”.
17. 将1,2,3,…,11;排成一圈,发现从中至多只能选取5个数保证菘中任意两数的差都不等于4或7;,所以我们尽可能选取1到9之间的数,以便使多一个完整的周期.经尝试选取数为:1,3,4,6,9;检验,,,,发现相邻周期间也不存在不满足题意的两数.所以当时,,,,,这915个数满足条件且为最多.
18. 设任意两名同台演出n次,;当时,m最小为7,将7人编号为1,2,…,7,7场演出如下:(1,2,4),(2,3,5),(3,4,6),(4,5,7),(5,6,1),(6,7,2),(7,1,3).
19. 提示:通过余数进行讨论.
20. 数字1、2、3、4、5、6各一张的选法有36种,其中三色不全的选法有.
故满足条件的选法有种.
自招链接
21. 根据乘法原理,所有长方形总数为(个),包含☆的长方形有(个),所以不包含☆的长方形有(个).
22. 我们把所有的比分,画到直角坐标系里面.形成下图:
每个点可以向右或者向上走,即标数法.
所以一共14种可能性,而,所以,所求概率为.
知识要点
组合问题非常考验同学们的思维能力,其中组合计数、概率等问题是自招考试的高频考点,抽屉原理、染色问题、极端原理等偶尔也会出现.
一、乘法原理
一般地,如果完成一件事需要n个步骤(缺一不可),第1步有m1种不同的方法,第2步有m2种不同的方法,第3步有m3种不同的方法……第n步有mn种不同的方法,则完成这件事一共有种不同的方法.
乘法原理运用的范围:这件事要分几个彼此互不影响的独立步骤来完成,这几步是完成这件任务缺一不可,这样的问题可以使用乘法原理解决.我们可以简记为:“乘法分步,步步相关”.
二、加法原理
一般地,如果完成一件事有n类步骤(每一类中的任何一种方法都能独立完成这件事情),第1类有m1,种不同的方法,第2类有m2种不同的方法,第3类有m3种不同的方法……第n类有mn种不同的方法,则完成这件事一共有种不同的方法.
加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.
三、排列
在实际生活中经常会遇到这样的问题,就是要把一些事物排在一起,构成一列,计算有多少种排法,就是排列问题.在排的过程中,不仅与参与排列的事物有关,而且与各事物所在的先后顺序有关.
根据排列的定义,两个排列相同,指的是两个排列的元素完全相同,并且元素的排列顺序也相同.如果两个排列中,元素不完全相同,它们是不同的排列;如果两个排列中,虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.
排列的基本问题是计算排列的总个数.
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素的排列中取出m个元素的排列数,我们把它记做或.
.
四、组合
一般地,从n个不同元素中取出m个(m≤n)元素组成一组不计较组内各元素的次序,叫做从n个不同元素中取出m个元素的一个组合.
从排列和组合的定义可以知道,排列与元素的顺序有关,而组合与顺序无关.如果两个组合中的元素完全相同,那么不管元素的顺序如何,都是相同的组合,只有当两个组合中的元素不完全相同时.才是不同的组合.
从n个不同元素中取出m个元素(m≤n)的所有组合的个数,叫做从n个不同元素中取出m个不同元素的组合数.记作或.
例题精讲
1. 回答下列问题:
(1)在1~5的自然数可以组成的五位数共有几个?
(2)有3种染料给三行144列的方格网染色,一共有多少种染色方法(只列式,不计算)?至少取多少列方格,才能保证有两列方格染色完全相同?
(3)从十位同学中任意选取2名同学,一共有多少种选法?
(4)爸爸、妈妈、客人和我四人围着圆桌喝茶.若只考虑每人左邻的情况,问共有多少种不同的入座方法?
(5)图11-l中有六个点,任意三个点都不在一条直线上.请问:以这些点为顶点,一共可以连出多少个三角形?
(6)某铁路线上,在起点和终点之间原有7个车站,现在新增加了3个车站,这样需要增加几种不同的车票?
2. 6人同时被邀请参加一项活动.必须有人去,去几个人自行决定,共有多少种不同的去法?
3. 小明的妈妈给了小明9块一样的糖,让他在接下来的4天正好吃完,每天至少吃一块,则小明有多少种不同的吃糖方案?
4. 4个人进行篮球训练,互相传球接球,要求每个人接球后马上传给别人,开始由甲发球,并作为第一次传球,第五次传球后,球又回到甲手中,问有多少种传球方法?
5. 游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?
6. 给定一个15×15的方格表,将其中有公共边的方格称为相邻的.将某些相邻方格的中心用线段相连,得到一条不白交的闭折线.现知该折线关于方格表的一条对角线对称.证明:折线的长度不大于200.
7. 物体A和B放在坐标平面上同时移动,且每次移动一个单位长度,A从(0,0)开始移动每次以相同的可能性向右或向上移动,物体B从(5,7)开始移动,每次以相同的可能性向左或向下移动,问两物体相遇的可能性是多少?
8. 摄影师给8名同学照相,有两人合影,也有三人合影,若任意两名同学都恰好合影一次,问最少要拍多少张照片?
9. 某同学在暑假里做数学竞赛题,每天至少做一题,每星期至多做12题,一共做了7个星期,求证:该同学在连续的若干天里恰好做了12道题.
10. 平面上有20个点,在他们之间已连了n线段,若任意三点之间都至少有一条线段.求n的最小值.
11. 20个红球、17个白球,重量都是正整数.红球与白球重量之和相等,且都小于340.证明:一定可以取出一些红球和一些白球,使得这些红球重量之和等于这些白球重量之和(不能全取).
习题巩固
12. 某件工作需要钳工2人和电工2人共同完成.现有钳工3人、电工3人,另有1人钳工、电工都会.从7人中挑选4人完成这项工作,共有多少种方法?
13. 平面上10个两两相交的圆最多能将平面分割成多少个区域?
14. 在图中(单位:厘米):
(1)一共有几个长方形?
(2)所有这些长方形面积的和是多少?
15. 有11名外语翻译人员,其中5名是英语翻译员,4名是日语翻译员,另外两名英语、日语都精通.从中找出8人,使他们组成两个翻译小组,其中4人翻译英文,另4人翻译日文,这两个小组能同时工作.问这样的分配名单共可以开出多少张?
16. 假如电子计时器所显示的十个数字是“0126093028”这样一串数,它表示的是1月26日9时30分28秒.在这串数里,“0”出现了3次,“2”出现了2次,“1”、“3”、“6”、“8”、“9”各出现1次,而“4”、“5”、“7”没有出现.如果在电子计时器所显示的这串数里.“0”、“1”、“2”、“3”、“4”、“5”、“6”、“7”、“8”、“9”这十个数字都只出现一次,称它所表示的时刻为“十全时”.那么2016年一共有几个这样的“十全时”?
17. 从1,2,…,2011中选取n个数,使得其中任意两数的差都不等于4或7.求n的最大值.
18. 7名学生参加演出,学校为他们安排了m次演出,每次由其中3名同学同时登台演出,请你设计一种方案,使得7名学生中,任意两名同台演出的次数一样多,且使m最小.
19. 求证:任意9个整数中,必有5个整数,它们的和被5整除.
20. 有红、黄、蓝卡片各6张,分别写有数字1、2、3、4、5、6.从中选取6张,要求三色俱全,且数字1、2、3、4、5、6各一张,则不同的选法有多少种?
自招链接
21. 在右图中,不包含☆的长方形有 个.
22. 第二季“中国好声音”杨坤组某一学员和那英组某一学员进行一对一PK,9位专业评委依次给两位学员投票,最终杨坤组学员拿到5票,那英组学员拿到4票.请问在依次投票的过程中,杨坤组学员得票数一直严格大于那英组学员得票数的概率是多少?
参考答案
1. (1)根据乘法原理,5×5×5×5×5=3125.共有3125个.
(2)根据乘法原理,.
抽屉原理,从最坏的情况考虑取到的第一个是列.
(3).
(4)4个相异元素的环形排列问题,共有种不同的入座方法.
(5)因为任意三个点都不在一条直线上;
所以以这些点为顶点,一共可以连出个三角形.
(6)原来有车站7+2=9,现在有车站9+3=12.
考虑每两个站点之间的往返车票起始站和终点站互异,所以新增的车票种类为
种.
2. (法一)可以分为一人去、两人去、三人去、四人去、五人去、六人去六种情况,每种情况都是组合问题.
第一种情况有6种去法;
第二种情况有种去法;
第三种情况有种去法;
第四种情况有种去法;
第五种情况有种去法;
第六种情况有种去法.
根据加法原理,共有6+15+20+15+6+1=63种不同的去法.
(法二)每个人都有去或不去两种可能,因此共有26种可能,但必须有人去,即所有人都不去的情况必须排除,因此有种.
3. 插板法:9块一样的糖有8个间隔,要分成4份,需要3个问隔,所以有种方案.
4. 设第n次传球后,球又回到甲手中的传球方法有an种.可以想象前次传球,如果每一次传球都任选其他三人中的一人进行传球,即每次传球都有3种可能,由乘法原理,共有(种)传球方法.这些传球方法并不是都符合要求的,它们可以分为两类,一类是第次恰好传到甲手中,这有种传法,它们不符合要求,因为这样第n次无法再把球传给甲;另一类是第次传球,球不在甲手中,第n次持球人再将球传给甲,有an种传法.根据加法原理,有.
由于甲是发球者,一次传球后球又回到甲手中的传球方法是不存在的,所以.
利用递推关系可以得到:,,,.
这说明经过5次传球后,球仍回到甲手中的传球方法有60种.
本题也可以列表求解.
由于第n次传球后,球不在甲手中的传球方法,第n+1次传球后球就可能回到甲手中,所以只需求出第四次传球后,球不在甲手中的传法共有多少种.
第n次传球 传球的方法 球在甲手中的传球方法 球不在甲手中的传球方法
1 3 0 3
2 9 3 6
3 27 6 21
4 81 21 60
5 243 60 183
从表中可以看出经过五次传球后,球仍回到甲手中的传球方法共有60种.
5. 与类似题目找对应关系.
要保证售票员总能找得开零钱,必须保证每一位拿2元钱的小朋友前面的若干小朋友中,拿1元的要比拿2元的人数多,先将拿1元钱的小朋友看成是相同的,将拿2元钱的小朋友看成是相同的,可以利用斜直角三角模型.在图11-2中,每条小横线段代表1元钱的小朋友,每条小竖线段代表2元钱的小朋友,因为从A点沿格线走到B点,每次只能向右或向上走,无论到途中哪一点,只要不超过斜线,那么经过的小横线段都不少于小竖线段,所以本题相当于求右图中从A到B有多少种不同走法.使用标数法,可求出从A到B有42种走法.
但是由于10个小朋友互不相同,必须将他们排队,可以分成两步,第一步排拿2元的小朋友,5个人共有5!=120种排法;第二步排拿到1元的小朋友,也有120种排法,所以共有5!×5!=14400种排队方法.
这样,使售票员能找得开零钱的排队方法共有42×14400=604800种.
6. 因为闭折线不自交,可知它恰好经过对角线方格上的两个中心点.(因为闭所以有2个,因为不自交所以只能为2个.)那么可以得到这条闭折现一定不经过其他的13个对角线方格的中心点.将15×15的方格表黑白二染色,对角线染黑色,则黑色小方格一定比白色小方格多一个.又因为折线上的中心点所在的小方格是黑白交替出现的,所以闭折曲线上的黑点和白点个数是相等的.如果闭折线不经过13个黑点,那么他必然不经过12个白点.所以闭折线经过的中心点的个数最多不超过;也就是说,折线的长度不大于200.
7. 因为从A到B的距离为12,所以要移动6次,物体A和B才能相遇.
在6次移动中,不同的移动方式有种.
其中A和B能相遇的移动方式有
.
故A和B相遇的可能性为.
8. 设3人合影的有x张,两人合影的有y张,则
.
因为每两人都恰好合影一张,所以每人至多可拍3张合影.故等则x≤8,所以
.
将8人编号为1,2,3,4,5,6,7,8;
8张三人合影为:(1,2,4),(2,3,5),(3,4,6),(4,5,7),(5,6,8),(6,7,9),(7,8,2),(8,1,3);
4张二人合影为:(1,5),(2,6),(3,7),(4,8);
显然这12张照片满足条件,所以最少要拍12张.
9. 设前n天做了an;那么
,
.
上面这98个数不同的取值最多96种.所以其中必有两数相等.
不妨设,则.
这表明从第(i+1)天开始,到第j天这连续若干天里恰好做了12道题.
10. 设A点连出的线段数最少,且为k条(0≤k≤19);将20个点分为两组,一组为A点和所有与A相连的k个点,共(k+1)个点;另外一组为余下的点,为是个点;对于第一组的(k+1)个点,因为A点连出的最少为k,所以他们连出的最少为;对于第二组的是个点,他们都不和A点相连,那么如果选取A点和他们其中的两个点,那么这三点之间至少有一条直线,于是第二组的是个点必须两两相连,共有条线.两者相加最少为.所以.
整理得:当且仅当k=9时取“=”.
下面构造一种方法证明90是可以的:20个点分为2组,每组10个点.同组的两两相连,不同组的不连.共连满足题意;
综上:n的最小值为90.
11. 对20个红球、17个白球的重量做排序,,记,由已知条件知.
考虑共340个元素,由抽屉原理,它们模339必有两个是同余的,不妨设
,
那么.
又因为,,所以,也就是得到了
,
命题得证.
习题巩固
12. 分两类情况讨论:
(1)都会的这1人被挑选中,则有:
①如果这人做钳工的话,则再按乘法原理,先选一名钳工有3种方法,再选2名电工也有3种方法,所以有33=9种方法.
②同样,这人做电工,也有9种方法.
(2)都会的这一人没有被挑选,则从3名钳工中选2人,有3种方法,从3名电工中选2人,也有3种方法,一共有33=9种方法.
所以,根据加法原理,一共有9+9+9=27种方法.
13. 先考虑最简单的情形,为了叙述方便,设平面上k个圆最多能将平面分割成ak个部分.
从图1中可以看出,,,,,…
可以发现ak满足下列关系式:.
实际上,当平面上的个圆把平面分成个区域时,如果再在平面上出现第k个圆,为了保证划分平面的区域尽可能多,新添的第k个圆不能通过平面上前个圆之间的交点.这样,第k个圆与前面个圆共产生个交点,如图2:
这个交点把第k个圆分成了段圆弧,而这段圆弧中的每一段都将所在的区域一分为二,所以也就是整个平面的区域数增加了个部分.所以,.
那么,
故10个圆最多能将平面分成92部分.
14. (1)一共有(个)长方形;
(2)所求的和是
(平方厘米).
15. 针对两名英语、日语都精通人员(以下称多面手)的参与情况分成三类:
(1)多面手不参加,则需从5名英语翻译员中选出4人,有种选择,需从4名日语翻译员中选出4人,有1种选择.由乘法原理,有种选择.
(2)多面手中有一人参加,有2种选择,而选出的这个人又有参加英文或日文翻译两种可能:
①如果参加英文翻译,则需从5名英语翻译员中再选出3人,有选择,需从4名日语翻译员中选出4人,有1种选择,由乘法原理,有种选择;
②如果参加日文翻译,则需从5名英语翻译员中选出4人,有种选择,需从4名日语翻译员中再选出3名,有种选择,由乘法原理,有种选择.
根据加法原理,多面手中有一人参加,有种选择.
(3)多面手中两人均参加,有一种选择,但此时又分三种情况:
①两人都译英文,②两人都译日文,③两人各译一个语种.
情况①中,还需从5名英语翻译员中选出2人,有种选择,需从4名日语翻译员中选4人,有1种选择.由乘法原理,有种选择.
情况②中,需从5名英语翻译员中选出4人,有种选择,还需从4名日语翻译员中选出2人,有种选择.
根据乘法原理,共有种选择.
情况③中,两人各译一个语种,有两种安排即两种选择,剩下的需从5名英语翻译员中选出3人,有种选择,需从4名日语翻译员中选出3名,有种选择,由乘法原理,有种选择.
根据加法原理,多面手中两人均参加,一共有种选择.
综上所述,由加法原理,这样的分配名单共可以开出张.
16. (1)容易验证在1、2、10、11、12月内没有“十全时”
(2)3月里只有形式032 1 □ □ 符合条件,其中2个方格中可以填4或5,4条横线上可以填6或7或8或9,所以3月里有个“十全时”.
同理,4、5月里各有48个“十全时”.
(3)6月里有2种形式:①061 23□ □ ,②062 1 □ □ .
①061 23□ □ 中,2个方格中可以填4或5,3条横线上可以填7或8或9,
②062 1 □ □ 中,2个方格中可以填3或4或5,4条横线上可以填7或8或9或3、4、5中余下的某一个.
所以6月里有个“十全时”.
同理,7、8、9月里各有156个“十全时”.
综上所述,2016年一共有个这样的“十全时”.
17. 将1,2,3,…,11;排成一圈,发现从中至多只能选取5个数保证菘中任意两数的差都不等于4或7;,所以我们尽可能选取1到9之间的数,以便使多一个完整的周期.经尝试选取数为:1,3,4,6,9;检验,,,,发现相邻周期间也不存在不满足题意的两数.所以当时,,,,,这915个数满足条件且为最多.
18. 设任意两名同台演出n次,;当时,m最小为7,将7人编号为1,2,…,7,7场演出如下:(1,2,4),(2,3,5),(3,4,6),(4,5,7),(5,6,1),(6,7,2),(7,1,3).
19. 提示:通过余数进行讨论.
20. 数字1、2、3、4、5、6各一张的选法有36种,其中三色不全的选法有.
故满足条件的选法有种.
自招链接
21. 根据乘法原理,所有长方形总数为(个),包含☆的长方形有(个),所以不包含☆的长方形有(个).
22. 我们把所有的比分,画到直角坐标系里面.形成下图:
每个点可以向右或者向上走,即标数法.
所以一共14种可能性,而,所以,所求概率为.
同课章节目录
