人教A版(2019)选择性必修第一册1.4.1.3空间中直线、平面的垂直 同步练习(Word版含答案)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册1.4.1.3空间中直线、平面的垂直 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 00:00:00 | ||
图片预览

文档简介
空间中直线、平面的垂直2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册
基础题
1.已知两直线的方向向量为a,b,则下列选项中能使两直线垂直的为( )
A.a=(1,0,0),b=(-3,0,0)
B.a=(0,1,0),b=(1,0,1)
C.a=(0,1,-1),b=(0,-1,1)
D.a=(1,0,0),b=(-1,0,0)
2.设直线l1,l2的方向向量分别为a=(-2,2,1),b=(3,-2,m),若l1⊥l2,则m等于( )
A.-2 B.2
C.6 D.10
3.已知平面α的法向量为a=(1,2,-2),平面β的法向量为b=(-2,-4,k),若α⊥β,则k等于( )
A.4 B.-4
C.5 D.-5
4.已知点A(0,1,0),B(-1,0,-1),C(2,1,1),P(x,0,z),若PA⊥平面ABC,则点P的坐标为( )
A.(1,0,-2) B.(1,0,2)
C.(-1,0,2) D.(2,0,-1)
5.(多选)给出下列命题,其中是真命题的是( )
A.若直线l的方向向量a=(1,-1,2),直线m的方向向量b=(2,1,-),则l与m垂直
B.若直线l的方向向量a=(0,1,-1),平面α的法向量n=(1,-1,-1),则l⊥α
C.若平面α,β的法向量分别为n1=(0,1,3),n2=(1,0,2),则α⊥β
D.若平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则u+t=1
6.已知直线l与平面α垂直,直线l的一个方向向量u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z=________.
7.在空间直角坐标系中,已知直角三角形ABC的三个顶点为A(-3,-2,1),B(-1,-1,-1),C(-5,x,0),则x的值为________.
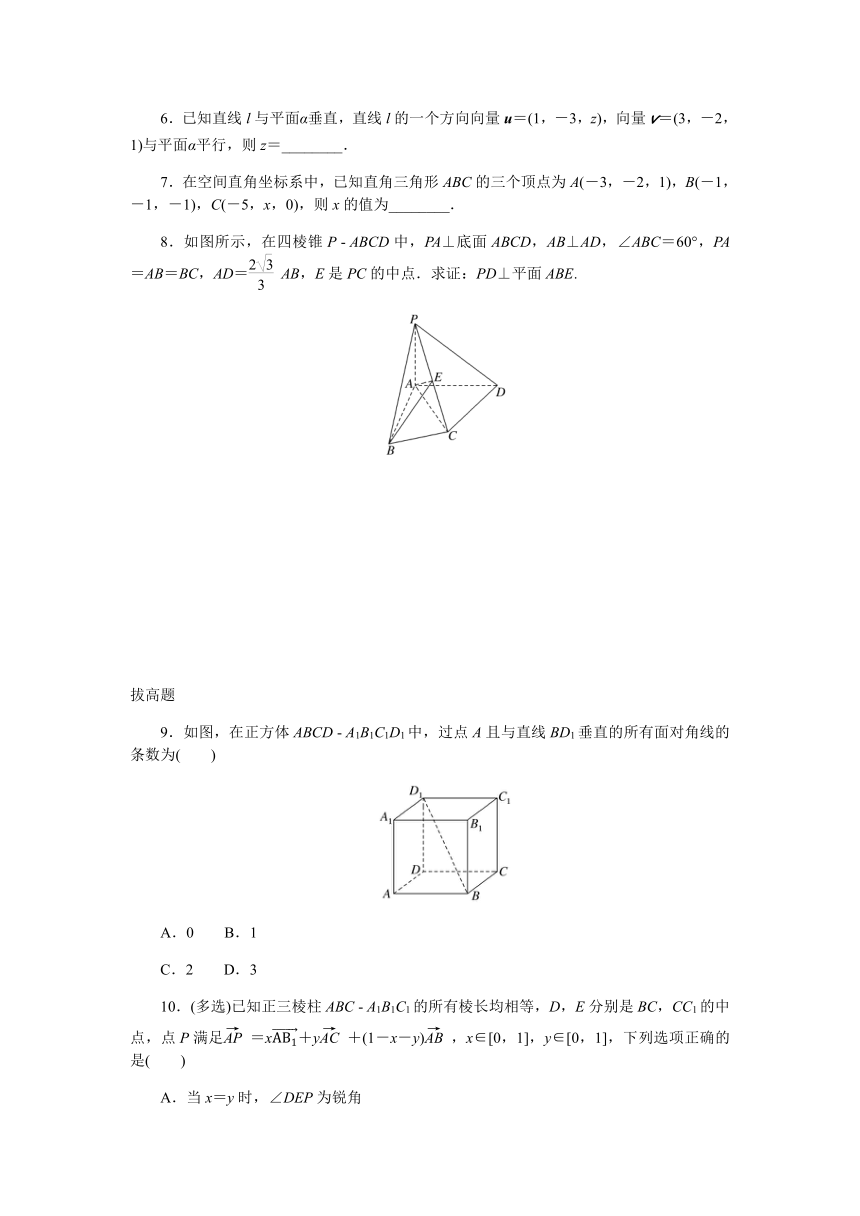
8.如图所示,在四棱锥P ABCD中,PA⊥底面ABCD,AB⊥AD,∠ABC=60°,PA=AB=BC,AD=AB,E是PC的中点.求证:PD⊥平面ABE.
拔高题
9.如图,在正方体ABCD A1B1C1D1中,过点A且与直线BD1垂直的所有面对角线的条数为( )
A.0 B.1
C.2 D.3
10.(多选)已知正三棱柱ABC A1B1C1的所有棱长均相等,D,E分别是BC,CC1的中点,点P满足=x+y+(1-x-y),x∈[0,1],y∈[0,1],下列选项正确的是( )
A.当x=y时,∠DEP为锐角
B.当x+2y=1时,AP⊥BE
C.当y=时,有且仅有一个点P,使得A1P⊥BP
D.当x-y=时,A1P∥平面ADE
11.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n与平面ABC垂直,且|n|=,则n的坐标为______________.
12.已知正方体ABCD A1B1C1D1中,E为棱CC1上的动点.
(1)求证:A1E⊥BD;
(2)若平面A1BD⊥平面EBD,试确定E点的位置.
能力题
13.(多选)如图,在三棱柱ABC A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是直线AD与A1C1的交点.若点Q在直线B1P上,则下列结论不正确的是( )
A.当点Q为线段B1P的中点时,DQ⊥平面A1BD
B.当点Q为线段B1P的三等分点(靠近点P)时,DQ⊥平面A1BD
C.在线段B1P的延长线上,存在一点Q,使得DQ⊥平面A1BD
D.在直线B1P上不存在点Q,使得DQ⊥平面A1BD
答案
1.B
2.D
3.D
4.C
5.AD
6.-9
7.0或9
8.证明:∵PA⊥底面ABCD,AB⊥AD,
∴AB,AD,AP两两垂直,建立如图所示的空间直角坐标系,设PA=AB=BC=1,则P(0,0,1),A(0,0,0),B(1,0,0),D
∵∠ABC=60°,
∴△ABC为正三角形.
∴C,E.
∴=(1,0,0),=,
∴设平面ABE的一个法向量为n=(x,y,z),
则,即,
令y=2,则z=-,∴n=(0,2,-).
∵=,显然=n,
∴∥n,
∴⊥平面ABE,即PD⊥平面ABE.
9.C
10.BD
11.(-2,4,1)或(2,-4,-1)
12.以D为坐标原点,以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图,
设正方体的棱长为a,则A(a,0,0),B(a,a,0),C(0,a,0),A1(a,0,a),C1(0,a,a).
设E(0,a,e)(0≤e≤a).
(1)证明:=(-a,a,e-a),=(-a,-a,0),
∵·=a2-a2+(e-a)·0=0,
∴⊥,即A1E⊥BD;
(2)设平面A1BD,平面EBD的法向量分别为n1=(x1,y1,z1),n2=(x2,y2,z2).
∵=(a,a,0),DA1=(a,0,a),=(0,a,e)
∴n1·=0,n1·DA1=0,n2·=0,n2·=0.
∴
取x1=x2=1,得n1=(1,-1,-1),n2=(1,-1,).
由平面A1BD⊥平面EBD得n1⊥n2.
∴2-=0,即e=.
∴当E为CC1的中点时,平面A1BD⊥平面EBD.
13.ABC
基础题
1.已知两直线的方向向量为a,b,则下列选项中能使两直线垂直的为( )
A.a=(1,0,0),b=(-3,0,0)
B.a=(0,1,0),b=(1,0,1)
C.a=(0,1,-1),b=(0,-1,1)
D.a=(1,0,0),b=(-1,0,0)
2.设直线l1,l2的方向向量分别为a=(-2,2,1),b=(3,-2,m),若l1⊥l2,则m等于( )
A.-2 B.2
C.6 D.10
3.已知平面α的法向量为a=(1,2,-2),平面β的法向量为b=(-2,-4,k),若α⊥β,则k等于( )
A.4 B.-4
C.5 D.-5
4.已知点A(0,1,0),B(-1,0,-1),C(2,1,1),P(x,0,z),若PA⊥平面ABC,则点P的坐标为( )
A.(1,0,-2) B.(1,0,2)
C.(-1,0,2) D.(2,0,-1)
5.(多选)给出下列命题,其中是真命题的是( )
A.若直线l的方向向量a=(1,-1,2),直线m的方向向量b=(2,1,-),则l与m垂直
B.若直线l的方向向量a=(0,1,-1),平面α的法向量n=(1,-1,-1),则l⊥α
C.若平面α,β的法向量分别为n1=(0,1,3),n2=(1,0,2),则α⊥β
D.若平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则u+t=1
6.已知直线l与平面α垂直,直线l的一个方向向量u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z=________.
7.在空间直角坐标系中,已知直角三角形ABC的三个顶点为A(-3,-2,1),B(-1,-1,-1),C(-5,x,0),则x的值为________.
8.如图所示,在四棱锥P ABCD中,PA⊥底面ABCD,AB⊥AD,∠ABC=60°,PA=AB=BC,AD=AB,E是PC的中点.求证:PD⊥平面ABE.
拔高题
9.如图,在正方体ABCD A1B1C1D1中,过点A且与直线BD1垂直的所有面对角线的条数为( )
A.0 B.1
C.2 D.3
10.(多选)已知正三棱柱ABC A1B1C1的所有棱长均相等,D,E分别是BC,CC1的中点,点P满足=x+y+(1-x-y),x∈[0,1],y∈[0,1],下列选项正确的是( )
A.当x=y时,∠DEP为锐角
B.当x+2y=1时,AP⊥BE
C.当y=时,有且仅有一个点P,使得A1P⊥BP
D.当x-y=时,A1P∥平面ADE
11.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n与平面ABC垂直,且|n|=,则n的坐标为______________.
12.已知正方体ABCD A1B1C1D1中,E为棱CC1上的动点.
(1)求证:A1E⊥BD;
(2)若平面A1BD⊥平面EBD,试确定E点的位置.
能力题
13.(多选)如图,在三棱柱ABC A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是直线AD与A1C1的交点.若点Q在直线B1P上,则下列结论不正确的是( )
A.当点Q为线段B1P的中点时,DQ⊥平面A1BD
B.当点Q为线段B1P的三等分点(靠近点P)时,DQ⊥平面A1BD
C.在线段B1P的延长线上,存在一点Q,使得DQ⊥平面A1BD
D.在直线B1P上不存在点Q,使得DQ⊥平面A1BD
答案
1.B
2.D
3.D
4.C
5.AD
6.-9
7.0或9
8.证明:∵PA⊥底面ABCD,AB⊥AD,
∴AB,AD,AP两两垂直,建立如图所示的空间直角坐标系,设PA=AB=BC=1,则P(0,0,1),A(0,0,0),B(1,0,0),D
∵∠ABC=60°,
∴△ABC为正三角形.
∴C,E.
∴=(1,0,0),=,
∴设平面ABE的一个法向量为n=(x,y,z),
则,即,
令y=2,则z=-,∴n=(0,2,-).
∵=,显然=n,
∴∥n,
∴⊥平面ABE,即PD⊥平面ABE.
9.C
10.BD
11.(-2,4,1)或(2,-4,-1)
12.以D为坐标原点,以DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,如图,
设正方体的棱长为a,则A(a,0,0),B(a,a,0),C(0,a,0),A1(a,0,a),C1(0,a,a).
设E(0,a,e)(0≤e≤a).
(1)证明:=(-a,a,e-a),=(-a,-a,0),
∵·=a2-a2+(e-a)·0=0,
∴⊥,即A1E⊥BD;
(2)设平面A1BD,平面EBD的法向量分别为n1=(x1,y1,z1),n2=(x2,y2,z2).
∵=(a,a,0),DA1=(a,0,a),=(0,a,e)
∴n1·=0,n1·DA1=0,n2·=0,n2·=0.
∴
取x1=x2=1,得n1=(1,-1,-1),n2=(1,-1,).
由平面A1BD⊥平面EBD得n1⊥n2.
∴2-=0,即e=.
∴当E为CC1的中点时,平面A1BD⊥平面EBD.
13.ABC
