人教版九年级上册24.1.3 弧、弦、圆心角课件(共26张PPT)
文档属性
| 名称 | 人教版九年级上册24.1.3 弧、弦、圆心角课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
课程:数学
《弧、弦、圆心角》
人教版
九年级上册 第3课时
第 24 章 圆
教学目标
1
2
3
知识与技能
1.理解圆心角概念和圆的旋转不变性.
2.掌握在同圆或等圆中,圆心角、弧、弦之间的关系,以及它们在解题过程中的应用.
过程与方法
通过学生动手或计算机演示使学生感受圆的旋转不变性,发展学生的观察分析能力.
情感态度和价值观
渗透初步的辩证唯物主义思想教育,使学生受到数学思想方法的熏陶,培养乐于学习、乐于探究的学习态度。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
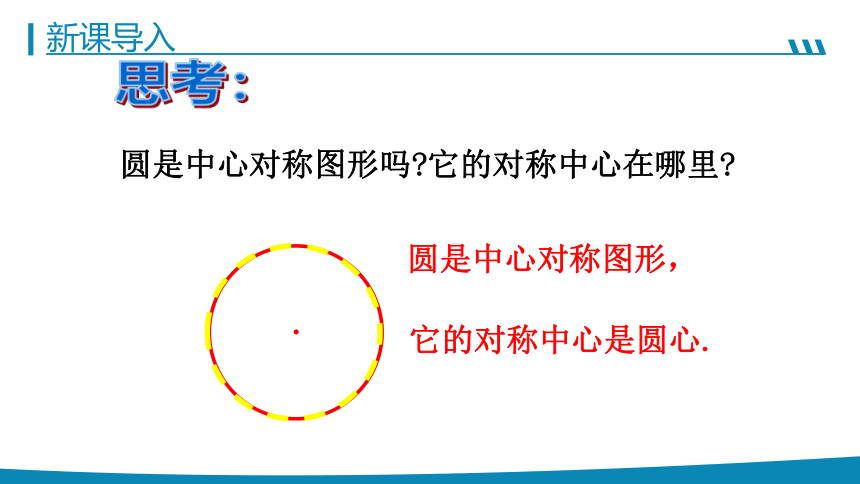
新课导入
圆是中心对称图形吗 它的对称中心在哪里
·
圆是中心对称图形,
它的对称中心是圆心.
思考:
02
PART TWO
探究新知
Explore new knowledge
圆心角:我们把 的角叫做圆心角.
探究新知
·
O
B
A
∠AOB是圆心角吗?
概念:
圆心角∠AOB所对的弦为AB,所对的弧为AB。
⌒
顶点在圆心
是
探究新知
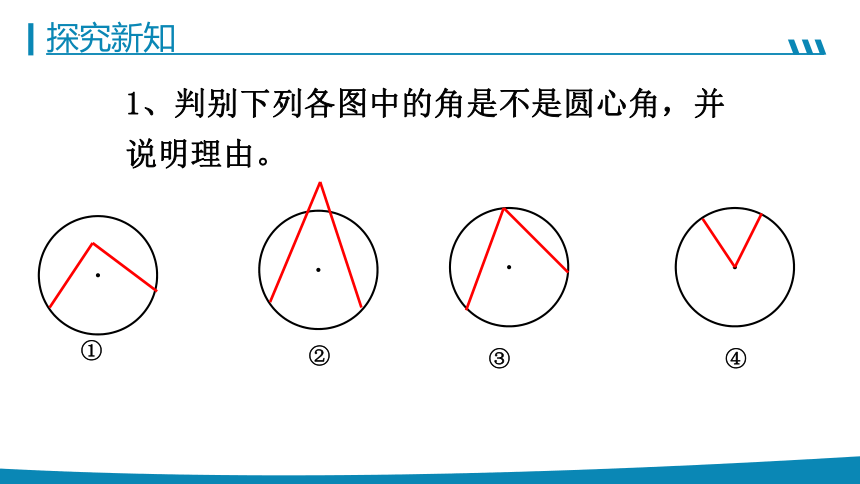
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
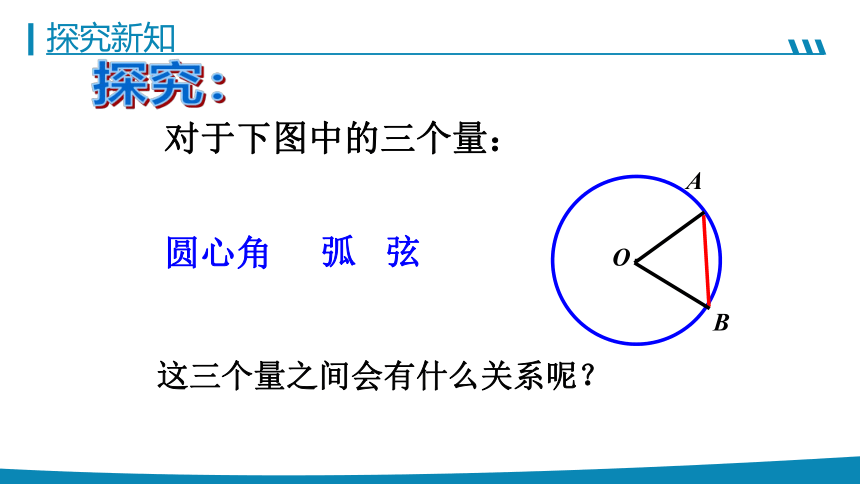
探究新知
对于下图中的三个量:
圆心角
弧
弦
·
O
B
A
探究:
这三个量之间会有什么关系呢?
探究新知
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
C
探究新知
·
O
A
B
探究一
思考:如图,在等圆中,如果∠AOB=∠A′O ′ B′,
你发现的等量关系是否依然成立?为什么?
·
O ′
A′
B′
由∠AOB=∠A′O ′ B′可得到:
探究新知
下面的说法正确吗 为什么
如图,因为
根据圆心角、弧、弦、
的关系可知:
⌒
⌒
探究新知
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
归纳:
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
圆心角定理
探究新知
(1)、如果 那么∠AOB=∠A′OB′, 成立吗
探究二
在同圆中,
(1)
成 立
探究新知
(2)、如果 那么∠AOB=∠A′OB′, 成立吗
探究二
在同圆中,
(2)
成 立
探究新知
(1) 圆心角
(2) 弧
(3) 弦
知一得二
等对等定理整体理解:
O
α
A
B
A1
B1
α
PART THREE
课堂练习
class exercise
03
课堂练习
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
OE﹦OF
探究新知
证明:
∴ AB=AC.⊿ABC是等腰三角形
又∠ACB=60°,
∴ ⊿ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC
60°
⌒ ⌒
∵
探究新知
3、如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
∵
探究新知
拓展点二与弧、弦、圆心角之间的关系有关的计算题
例2 如图,在△AOB中,AO=AB,以点O为圆心,OB为半径的圆交AB于点D,交AO于点E,AD=OB.试说明 ,并求∠A的度数.
探究新知
解:连接OD,如图所示,设∠A=x,
∵AD=OB,∴DO=DA,
∴∠DOA=x,
∴∠BDO=2x,
∴∠B=2x,又∵AO=AB,
∴∠BOE=∠B=2x,
∴∠BOD=2x-x=x=∠DOE,
∴ .在△OBD中,x+2x+2x=180°,
∴x=36°,即∠A=36°.
探究新知
如图,已知BD,CE是☉O的两条弦,OA平分∠DAE.求证:AB=AC.
分析:作OM⊥BD于M,ON⊥CE于N,根据角平分线的性质得到OM=ON,根据圆心角、弧、弦之间的关系得到BD=CE,证明△AMO≌△ANO,得到AM=AN,得到答案.
探究新知
证明:作OM⊥BD于M,ON⊥CE于N,
∵OA平分∠DAE,∴OM=ON,∴BD=CE.
∵OM⊥BD,ON⊥CE,
∴△AMO≌△ANO,∴AM=AN,∴AB=AC.
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
弧、弦与圆心角的关系定理
1、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角
相等
弧
相等
弦
相等
2、在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
3、在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.
相等
相等
相等
相等
在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
课程:数学
《弧、弦、圆心角》
人教版
九年级上册 第3课时
第 24 章 圆
教学目标
1
2
3
知识与技能
1.理解圆心角概念和圆的旋转不变性.
2.掌握在同圆或等圆中,圆心角、弧、弦之间的关系,以及它们在解题过程中的应用.
过程与方法
通过学生动手或计算机演示使学生感受圆的旋转不变性,发展学生的观察分析能力.
情感态度和价值观
渗透初步的辩证唯物主义思想教育,使学生受到数学思想方法的熏陶,培养乐于学习、乐于探究的学习态度。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
圆是中心对称图形吗 它的对称中心在哪里
·
圆是中心对称图形,
它的对称中心是圆心.
思考:
02
PART TWO
探究新知
Explore new knowledge
圆心角:我们把 的角叫做圆心角.
探究新知
·
O
B
A
∠AOB是圆心角吗?
概念:
圆心角∠AOB所对的弦为AB,所对的弧为AB。
⌒
顶点在圆心
是
探究新知
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
探究新知
对于下图中的三个量:
圆心角
弧
弦
·
O
B
A
探究:
这三个量之间会有什么关系呢?
探究新知
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
C
探究新知
·
O
A
B
探究一
思考:如图,在等圆中,如果∠AOB=∠A′O ′ B′,
你发现的等量关系是否依然成立?为什么?
·
O ′
A′
B′
由∠AOB=∠A′O ′ B′可得到:
探究新知
下面的说法正确吗 为什么
如图,因为
根据圆心角、弧、弦、
的关系可知:
⌒
⌒
探究新知
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
归纳:
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
圆心角定理
探究新知
(1)、如果 那么∠AOB=∠A′OB′, 成立吗
探究二
在同圆中,
(1)
成 立
探究新知
(2)、如果 那么∠AOB=∠A′OB′, 成立吗
探究二
在同圆中,
(2)
成 立
探究新知
(1) 圆心角
(2) 弧
(3) 弦
知一得二
等对等定理整体理解:
O
α
A
B
A1
B1
α
PART THREE
课堂练习
class exercise
03
课堂练习
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
OE﹦OF
探究新知
证明:
∴ AB=AC.⊿ABC是等腰三角形
又∠ACB=60°,
∴ ⊿ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC
60°
⌒ ⌒
∵
探究新知
3、如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
解:
∵
探究新知
拓展点二与弧、弦、圆心角之间的关系有关的计算题
例2 如图,在△AOB中,AO=AB,以点O为圆心,OB为半径的圆交AB于点D,交AO于点E,AD=OB.试说明 ,并求∠A的度数.
探究新知
解:连接OD,如图所示,设∠A=x,
∵AD=OB,∴DO=DA,
∴∠DOA=x,
∴∠BDO=2x,
∴∠B=2x,又∵AO=AB,
∴∠BOE=∠B=2x,
∴∠BOD=2x-x=x=∠DOE,
∴ .在△OBD中,x+2x+2x=180°,
∴x=36°,即∠A=36°.
探究新知
如图,已知BD,CE是☉O的两条弦,OA平分∠DAE.求证:AB=AC.
分析:作OM⊥BD于M,ON⊥CE于N,根据角平分线的性质得到OM=ON,根据圆心角、弧、弦之间的关系得到BD=CE,证明△AMO≌△ANO,得到AM=AN,得到答案.
探究新知
证明:作OM⊥BD于M,ON⊥CE于N,
∵OA平分∠DAE,∴OM=ON,∴BD=CE.
∵OM⊥BD,ON⊥CE,
∴△AMO≌△ANO,∴AM=AN,∴AB=AC.
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
弧、弦与圆心角的关系定理
1、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角
相等
弧
相等
弦
相等
2、在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
3、在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.
相等
相等
相等
相等
在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
同课章节目录
