2022—2023学年人教版数学九年级上册 24.2.1点和圆的位置关系 课件(共37张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册 24.2.1点和圆的位置关系 课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 08:26:51 | ||
图片预览





文档简介
(共37张PPT)
课程:数学
《点和圆的位置关系》
人教版
九年级上册 第5课时
第 24 章 圆
教学目标
1
2
3
知识与技能
理解点与圆的位置关系由点到圆心的距离决定,理解不在同一条直线上的三个点确定一个圆,会画三角形的外接圆,熟识相关概念.
过程与方法
经历探索点与圆的位置关系的过程,体会数学分类思考的数学思想.
情感态度和价值观
通过本节课的数学,渗透数形结合的思想和运动变化的观点的教育.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
A
B
C
D
E
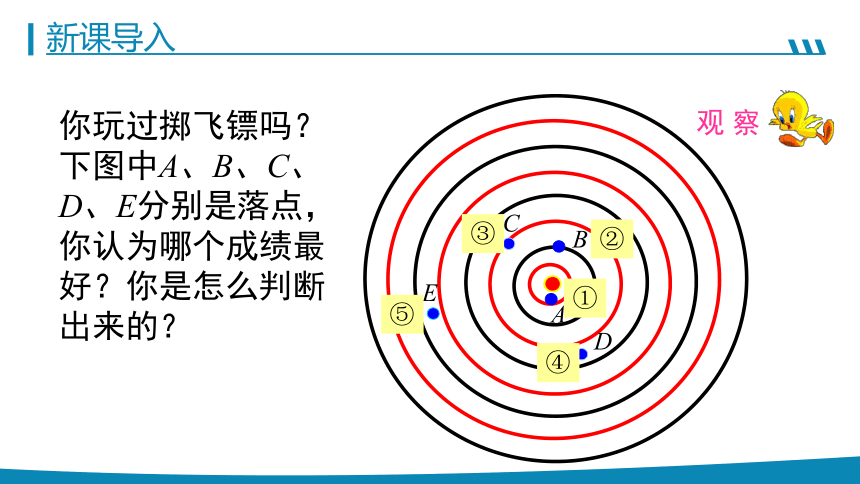
你玩过掷飞镖吗?下图中A、B、C、D、E分别是落点,你认为哪个成绩最好?你是怎么判断出来的?
观 察
①
②
③
④
⑤
02
PART TWO
探究新知
Explore new knowledge
探究新知
O
r
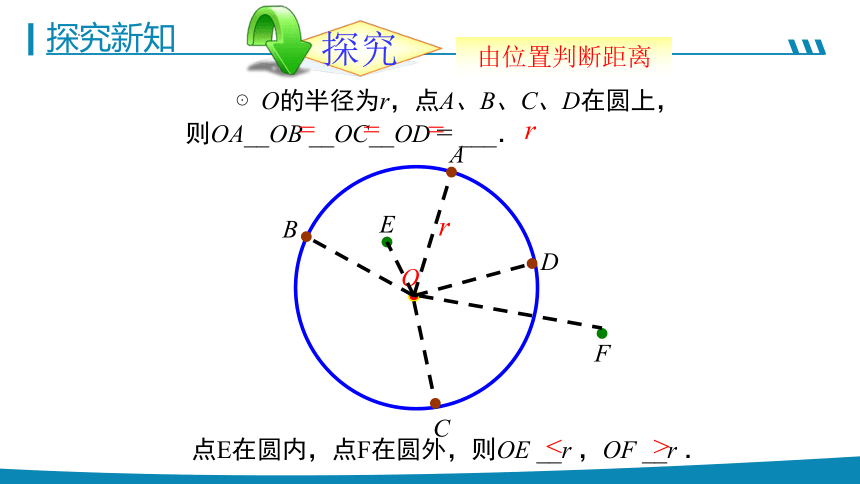
⊙O的半径为r,点A、B、C、D在圆上,则OA__OB __OC__OD = ___.
=
=
=
r
B
A
D
C
E
F
点E在圆内,点F在圆外,则OE __r ,OF __r .
<
>
探究
由位置判断距离
探究新知
O
探究
A
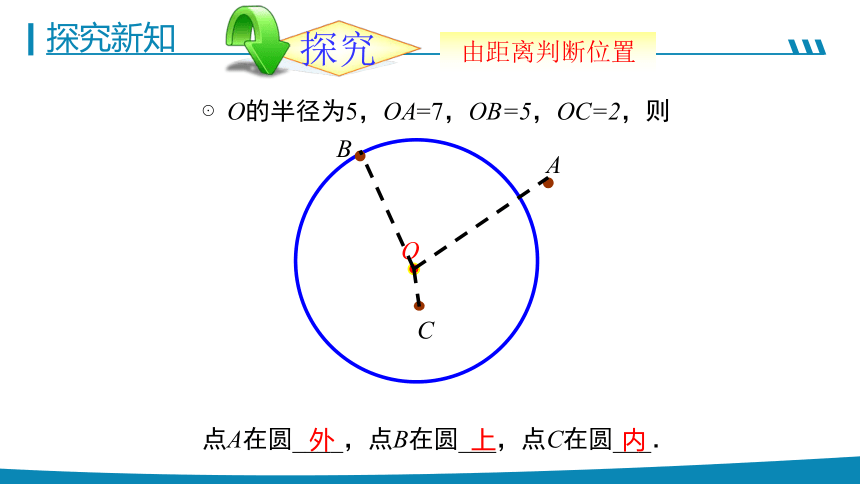
点A在圆____,点B在圆___,点C在圆___.
内
外
由距离判断位置
B
C
⊙O的半径为5,OA=7,OB=5,OC=2,则
上
探究新知
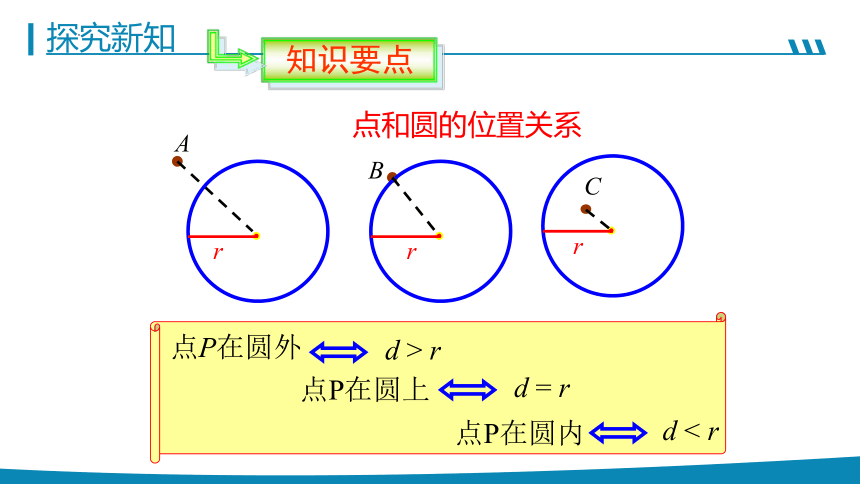
点P在圆外
点P在圆上
点P在圆内
d < r
d = r
d > r
知识要点
点和圆的位置关系
A
B
C
r
r
r
探究新知
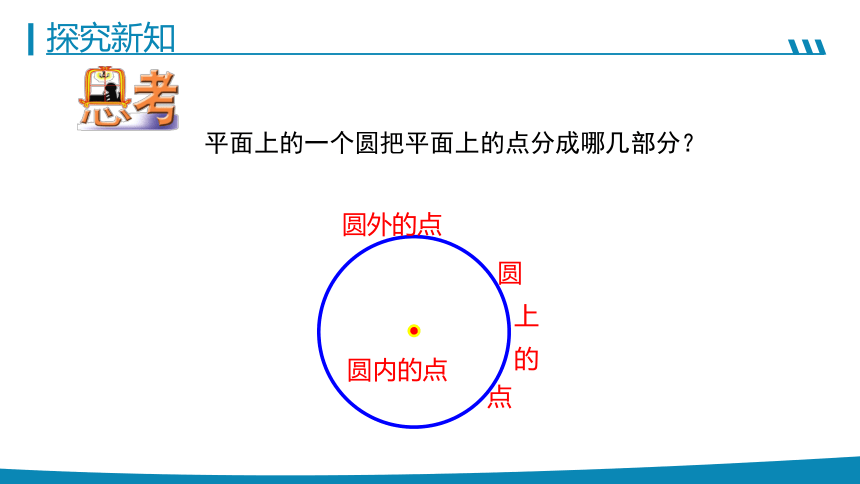
圆外的点
圆内的点
平面上的一个圆把平面上的点分成哪几部分?
圆
上
的
点
探究新知
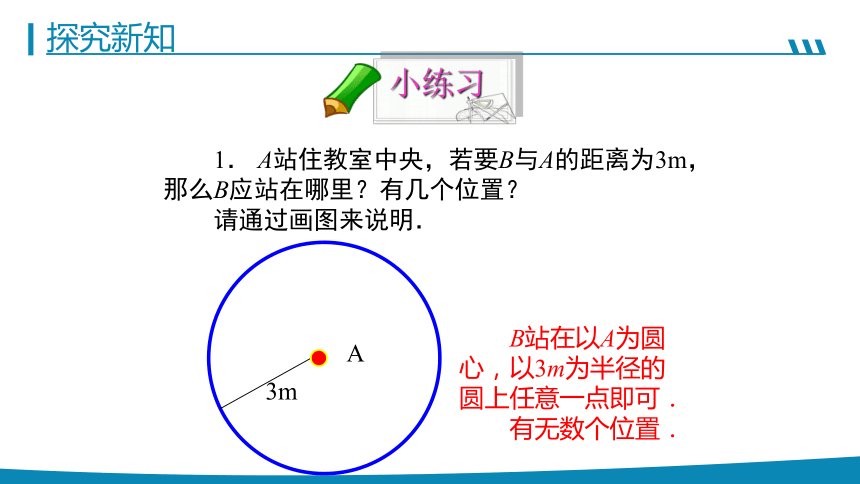
1. A站住教室中央,若要B与A的距离为3m,那么B应站在哪里?有几个位置?
请通过画图来说明.
小练习
3m
A
B站在以A为圆心,以3m为半径的圆上任意一点即可.
有无数个位置.
探究新知
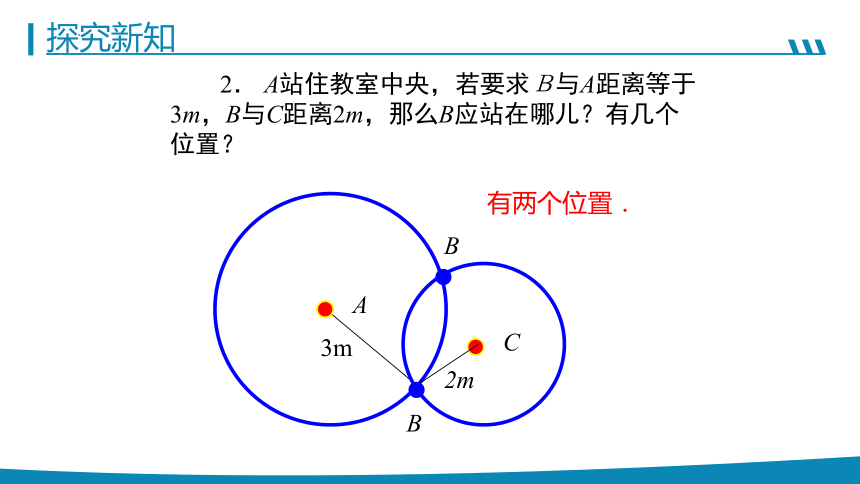
2. A站住教室中央,若要求B与A距离等于3m,B与C距离2m,那么B应站在哪儿?有几个位置?
3m
A
C
2m
B
B
有两个位置.
探究新知
3. 现在要求B与A距离3m以外,B与C距离2m以外,那么B应站在哪儿?有几个位置?
A
C
3m
2m
B应站在⊙A和⊙C的圆外 ,有无数个位置.
探究新知
画圆的关键是什么?
确定半径的大小
回 顾
确定圆心
探究新知
1. 过一点可以作几个圆
●O
●A
●O
●O
●O
●O
探究
无数个
点A以外任意一点
这点与点A的距离
圆心:
半径:
探究新知
2. 过两点可以作几个圆?
●A
●B
●O
●O
●O
●O
无数个
这点到A或B的距离
线段AB的垂直平分线上
圆心:
半径:
探究新知
3. 过不在同一条直线上的三点可以作几个圆
A
B
C
探究新知
经过A、B两点的圆的圆心在线段AB的垂直平分线上.
分析
A
B
C
步骤1
探究新知
经过B、C两点的圆的圆心在线段BC的垂直平分线上.
A
B
C
步骤2
探究新知
经过A、B、C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
A
B
C
步骤3
探究新知
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
知识要点
探究新知
O
外接圆、外心
A
B
C
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆(circumcircle of triangle).
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心(circumcenter).
探究新知
O
内接三角形
△ABC叫这个圆的内接三角形.
A
B
C
探究新知
A
B
C
不在同一直线上的三个点确定一个圆.
为什么要这样强调?经过同一直线的三点能作出一个圆吗?
探究新知
l
l1
l2
A
B
C
O
探究
证明:假设经过同一直线 l 的三个点能作出
一个圆,圆心 为O.
则O应在AB的垂直平分线l1上,
且O在BC的垂直平分线上l2上,
l1⊥ l
l2⊥ l
所以l1、 l2同时垂直于l,
这与“过一点有且只有一条直线垂直于已知直线”矛盾,
所以经过同一直线的三点不能作圆.
探究新知
反证法
假设命题的结论不成立,由此经过推理得出矛盾,由矛盾判定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
经过同一直线的三点不能作出一个圆.
命题:
假设:
经过同一直线的三点能作出一个圆.
矛盾:
过一点有且只有一条直线垂直于已知直线
过一点有两条直线垂直于已知直线.
定理:
例如:
探究新知
分别画锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,各三角形与它的外心有什么位置关系?
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
探究
PART THREE
课堂练习
class exercise
03
课堂练习
1. 判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆 ( )
(2)任意一个圆有且只有一个内接三角形 ( )
(3)经过三点一定可以确定一个圆 ( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
√
×
课堂练习
2. 若一个三角形的外心在一边上,则此三角形的形状为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
B
探究新知
3. ⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在_____;点B在_____ ;点C在________ .
4. ⊙O的半径6cm,当OP=6时,点A在____ ;当OP _____时点P在圆内;当OP _____ 时,点P不在圆外.
圆内
圆上
圆外
圆上
<6
≤6
探究新知
6. 已知AB为⊙O的直径P为⊙O 上任意一点,则点关于AB的对称点P′与⊙O的位置为( )
A. 在⊙O内 B. 在⊙O 外
C. 在⊙O 上 D. 不能确定
C
5. 正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A _____ ;点C在⊙A ____;点D在⊙A _____ .
上
外
上
探究新知
7. 已知⊙O的面积为9π,判断点P与⊙O的位置关系.
(1)若PO=4.5,则点P在_____;
(2)若PO=2,则点P在_____;
(3)若PO= _____,则点P在圆上.
圆外
圆内
3
8. 爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的的安全区域,已知这个导火索的长度为18cm,如果点导火索的人以每秒6.5m的速度撤离,那么是否安全?为什么?
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
点P在圆外
点P在圆上
点P在圆内
d < r
d = r
d > r
1. 点和圆的位置关系
A
B
C
r
r
r
课堂小结
这节课你们都学会了哪些知识?
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
2. 三点定圆
A
B
C
课堂小结
这节课你们都学会了哪些知识?
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫这个圆的内接三角形.
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
3. 外接圆、内接三角形
4. 外心
A
B
C
课程:数学
《点和圆的位置关系》
人教版
九年级上册 第5课时
第 24 章 圆
教学目标
1
2
3
知识与技能
理解点与圆的位置关系由点到圆心的距离决定,理解不在同一条直线上的三个点确定一个圆,会画三角形的外接圆,熟识相关概念.
过程与方法
经历探索点与圆的位置关系的过程,体会数学分类思考的数学思想.
情感态度和价值观
通过本节课的数学,渗透数形结合的思想和运动变化的观点的教育.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
A
B
C
D
E
你玩过掷飞镖吗?下图中A、B、C、D、E分别是落点,你认为哪个成绩最好?你是怎么判断出来的?
观 察
①
②
③
④
⑤
02
PART TWO
探究新知
Explore new knowledge
探究新知
O
r
⊙O的半径为r,点A、B、C、D在圆上,则OA__OB __OC__OD = ___.
=
=
=
r
B
A
D
C
E
F
点E在圆内,点F在圆外,则OE __r ,OF __r .
<
>
探究
由位置判断距离
探究新知
O
探究
A
点A在圆____,点B在圆___,点C在圆___.
内
外
由距离判断位置
B
C
⊙O的半径为5,OA=7,OB=5,OC=2,则
上
探究新知
点P在圆外
点P在圆上
点P在圆内
d < r
d = r
d > r
知识要点
点和圆的位置关系
A
B
C
r
r
r
探究新知
圆外的点
圆内的点
平面上的一个圆把平面上的点分成哪几部分?
圆
上
的
点
探究新知
1. A站住教室中央,若要B与A的距离为3m,那么B应站在哪里?有几个位置?
请通过画图来说明.
小练习
3m
A
B站在以A为圆心,以3m为半径的圆上任意一点即可.
有无数个位置.
探究新知
2. A站住教室中央,若要求B与A距离等于3m,B与C距离2m,那么B应站在哪儿?有几个位置?
3m
A
C
2m
B
B
有两个位置.
探究新知
3. 现在要求B与A距离3m以外,B与C距离2m以外,那么B应站在哪儿?有几个位置?
A
C
3m
2m
B应站在⊙A和⊙C的圆外 ,有无数个位置.
探究新知
画圆的关键是什么?
确定半径的大小
回 顾
确定圆心
探究新知
1. 过一点可以作几个圆
●O
●A
●O
●O
●O
●O
探究
无数个
点A以外任意一点
这点与点A的距离
圆心:
半径:
探究新知
2. 过两点可以作几个圆?
●A
●B
●O
●O
●O
●O
无数个
这点到A或B的距离
线段AB的垂直平分线上
圆心:
半径:
探究新知
3. 过不在同一条直线上的三点可以作几个圆
A
B
C
探究新知
经过A、B两点的圆的圆心在线段AB的垂直平分线上.
分析
A
B
C
步骤1
探究新知
经过B、C两点的圆的圆心在线段BC的垂直平分线上.
A
B
C
步骤2
探究新知
经过A、B、C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
A
B
C
步骤3
探究新知
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
知识要点
探究新知
O
外接圆、外心
A
B
C
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆(circumcircle of triangle).
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心(circumcenter).
探究新知
O
内接三角形
△ABC叫这个圆的内接三角形.
A
B
C
探究新知
A
B
C
不在同一直线上的三个点确定一个圆.
为什么要这样强调?经过同一直线的三点能作出一个圆吗?
探究新知
l
l1
l2
A
B
C
O
探究
证明:假设经过同一直线 l 的三个点能作出
一个圆,圆心 为O.
则O应在AB的垂直平分线l1上,
且O在BC的垂直平分线上l2上,
l1⊥ l
l2⊥ l
所以l1、 l2同时垂直于l,
这与“过一点有且只有一条直线垂直于已知直线”矛盾,
所以经过同一直线的三点不能作圆.
探究新知
反证法
假设命题的结论不成立,由此经过推理得出矛盾,由矛盾判定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
经过同一直线的三点不能作出一个圆.
命题:
假设:
经过同一直线的三点能作出一个圆.
矛盾:
过一点有且只有一条直线垂直于已知直线
过一点有两条直线垂直于已知直线.
定理:
例如:
探究新知
分别画锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,各三角形与它的外心有什么位置关系?
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
探究
PART THREE
课堂练习
class exercise
03
课堂练习
1. 判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆 ( )
(2)任意一个圆有且只有一个内接三角形 ( )
(3)经过三点一定可以确定一个圆 ( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
√
×
课堂练习
2. 若一个三角形的外心在一边上,则此三角形的形状为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
B
探究新知
3. ⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在_____;点B在_____ ;点C在________ .
4. ⊙O的半径6cm,当OP=6时,点A在____ ;当OP _____时点P在圆内;当OP _____ 时,点P不在圆外.
圆内
圆上
圆外
圆上
<6
≤6
探究新知
6. 已知AB为⊙O的直径P为⊙O 上任意一点,则点关于AB的对称点P′与⊙O的位置为( )
A. 在⊙O内 B. 在⊙O 外
C. 在⊙O 上 D. 不能确定
C
5. 正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A _____ ;点C在⊙A ____;点D在⊙A _____ .
上
外
上
探究新知
7. 已知⊙O的面积为9π,判断点P与⊙O的位置关系.
(1)若PO=4.5,则点P在_____;
(2)若PO=2,则点P在_____;
(3)若PO= _____,则点P在圆上.
圆外
圆内
3
8. 爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的的安全区域,已知这个导火索的长度为18cm,如果点导火索的人以每秒6.5m的速度撤离,那么是否安全?为什么?
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
点P在圆外
点P在圆上
点P在圆内
d < r
d = r
d > r
1. 点和圆的位置关系
A
B
C
r
r
r
课堂小结
这节课你们都学会了哪些知识?
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
2. 三点定圆
A
B
C
课堂小结
这节课你们都学会了哪些知识?
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫这个圆的内接三角形.
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
3. 外接圆、内接三角形
4. 外心
A
B
C
同课章节目录
