2022—2023学年人教版数学九年级上册 24.3正多边形和圆 课件 (共36张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册 24.3正多边形和圆 课件 (共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 08:36:15 | ||
图片预览





文档简介
(共36张PPT)
课程:数学
《正多边形和圆》
人教版
九年级上册 第8课时
第 24 章 圆
教学目标
1
2
3
知识与技能
使学生理解正多边形概念,了解依次连结圆的n等分点所得的多边形是正多边形;过圆的n等分点作圆的切线,以相邻切线的交点为顶点的多边形是正多边形。
过程与方法
通过正多边形定义教学培养学生归纳能力:通过正多边形与圆关系定理的教学培养学生观察、猜想、推理、迁移能力
情感态度和价值观
向学生渗透“特殊——一般”再“一般——特殊”的唯物辩证法思想。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
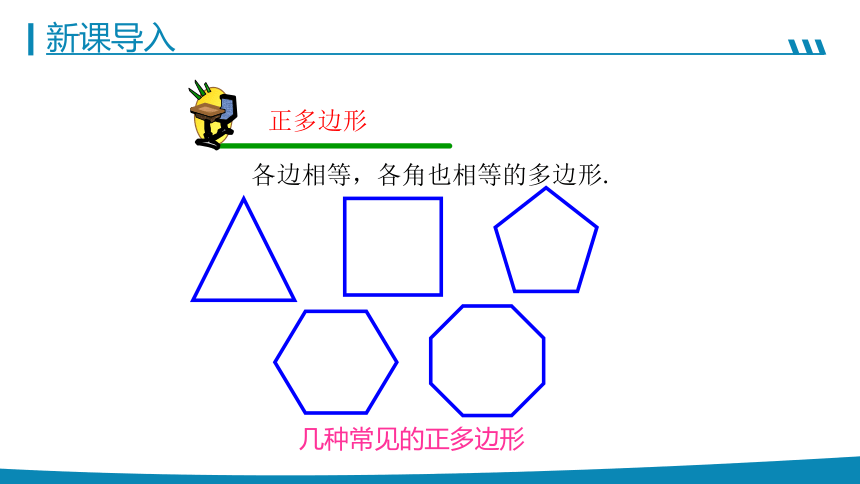
正多边形
各边相等,各角也相等的多边形.
几种常见的正多边形
02
PART TWO
探究新知
Explore new knowledge
探究新知
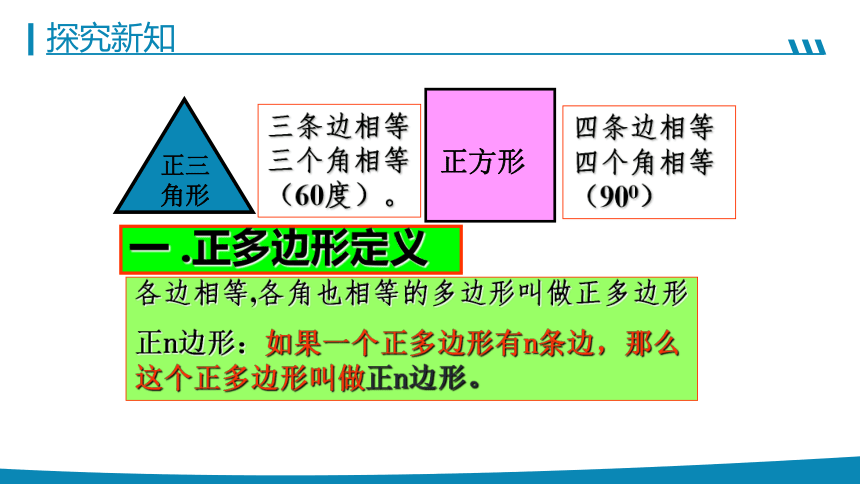
各边相等,各角也相等的多边形叫做正多边形
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
三条边相等三个角相等(60度)。
四条边相等四个角相等(900)
正三角形
正方形
一 .正多边形定义
探究新知
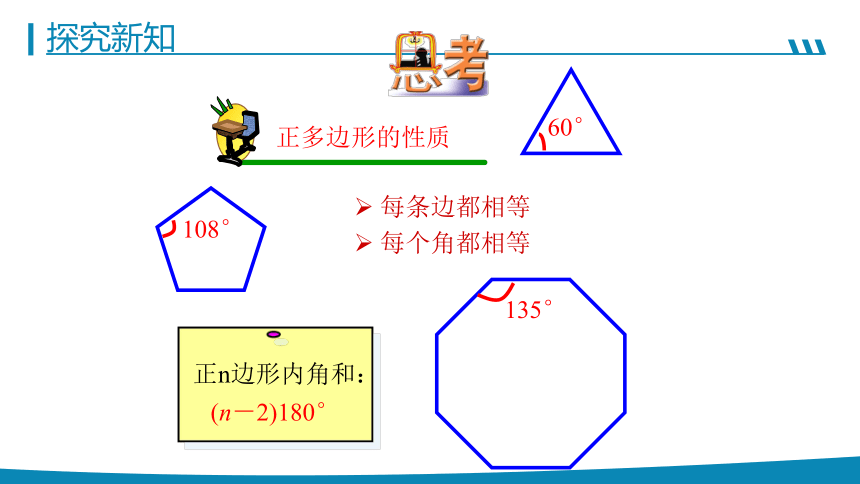
正多边形的性质
60°
正n边形内角和:
(n-2)180°
108°
每条边都相等
每个角都相等
135°
探究新知
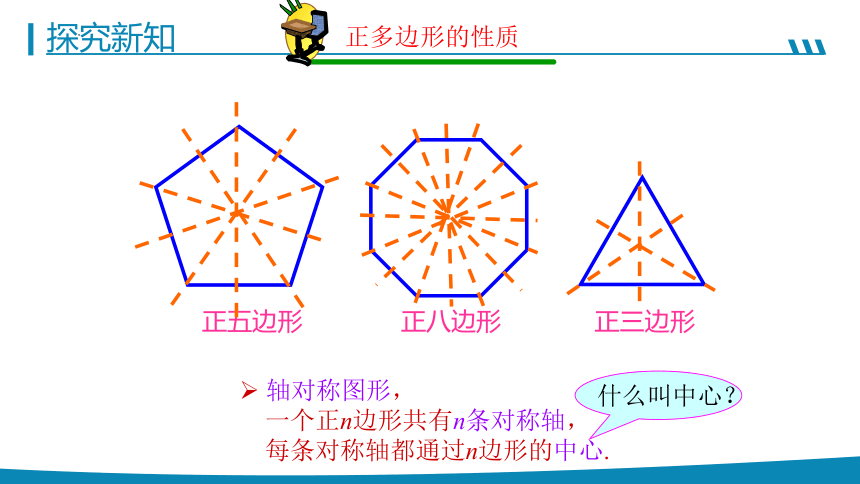
轴对称图形,
一个正n边形共有n条对称轴,
每条对称轴都通过n边形的中心.
正多边形的性质
正五边形
正八边形
正三边形
什么叫中心?
探究新知
边数是偶数的正多边形
是中心对称图形,
它的中心就是对称中心.
正八边形
正六边形
正多边形的性质
探究新知
菱形是正多边形吗?矩形是正多边形吗?
小练习
×
×
菱形的四个角不相等.
矩形的四条边不相等.
探究新知
C
A
B
D
E
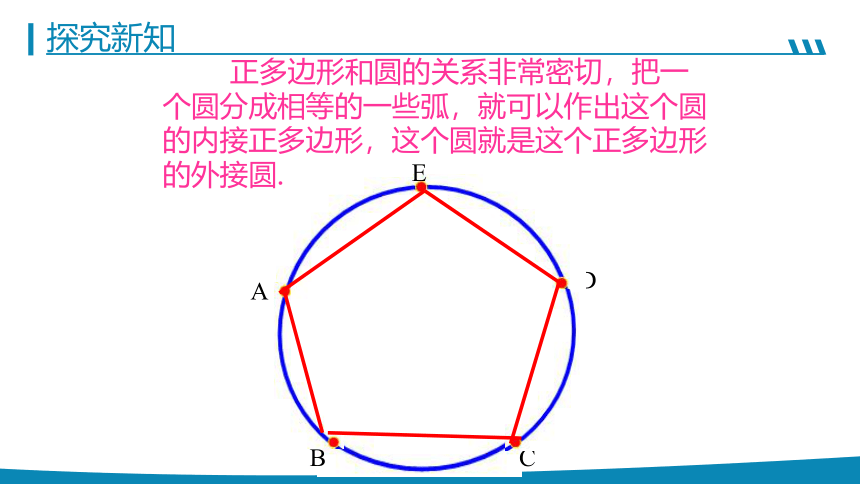
正多边形和圆的关系非常密切,把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
探究新知
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
证明:∵AB=BC=CD=DE=EA
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
∴∠1=∠2
同理∠2=∠3=∠4=∠5
又∵顶点A、B、C、D、E都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
⊙O是五边形ABCDE的外接圆.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
定理证明
探究新知
把圆分成 n(n≥3)等份:
依次连结各分点所得的多边形是这个圆的内接正多边形.
内接正多边形
探究新知
E
F
C
D
.
.
O
中心角
半径R
边心距
r
中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径.
正多边形的中心角:
正多边形的每一条边
所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
中心
正多边形及外接圆中的有关概念
探究新知
E
F
C
D
.
.
O
中心角
A
B
G
边心距OG把△AOB分成
2个全等的直角三角形.
设正多边形的边长为a,半径为R,它的周长为L = na.
R
a
正多边形的有关计算
探究新知
A
B
C
D
正多边形 外接圆
弦相等
多边形的边相等
多边形的角相等
圆周角相等
内接正多边形与外接圆的联系
探究新知
把正n边形的边数无限增多,
正多边形
……
就接近于圆.
圆
由圆怎样得到正多边形?
探究新知
把一个圆4等分,并依次连接这些点,得到正多边形吗
探究
正方形
探究新知
已知⊙O的半径为2cm,求作圆的内接正三角形
120 °
A
O
C
B
探究
①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
一题多解
量角器作图
探究新知
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
小练习
探究新知
你能用尺规作出正四边形、正八边形吗?
·
A
B
C
D
O
探究
尺规作图
作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
探究新知
你能用尺规作出正六边形、正三角形、正十二边形吗?
O
A
B
C
E
F
·
D
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
探究新知
有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
例题
探究新知
A
B
C
D
E
O
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接正五边形和外切正五边形.
小练习
探究新知
把圆分成 n(n≥3)等份:
经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正多边形.
外切正多边形
探究新知
又∵五边形PQRST的各边都与⊙O相切,
∴五边形PQRST的是O外切正五边形。
证明:连结OA、OB、OC,则:
∠OAB=∠OBA=∠OBC=∠OCB
∵TP、PQ、QR分别是以A、B、C
为切点的⊙O的切线
∴∠OAP=∠OBP=∠OBQ=∠OCQ
∴∠PAB=∠PBA=∠QBC=∠QCB
又∵AB=BC
∴AB=BC
∴△PAB与△QBC是全等的等腰三角形。
∴∠P=∠Q PQ=2PA
同理∠Q=∠R=∠S=∠T
QR=RS=ST=TP=2PA
⌒
⌒
A
B
C
D
E
P
Q
R
S
T
O
定理证明
PART THREE
课堂练习
class exercise
03
课堂练习
1. 正n边形的一个内角的度数是____________;
中心角是___________;正多边形的中心角与外角的
大小关系是________.
相等
2. O是正△ABC的中心,它是△ABC的________圆与________圆的圆心.
外接
内切
探究新知
3. OB叫正△ABC的________ ,它是正△ABC的________圆的半径.
4. OD叫作正△ABC的________ ,它是正△ABC的________ 圆的半径。
A
B
C
.O
D
半径
外接
边心距
内切
探究新知
A
B
C
D
E
5. 求证:正五边形的对角线相等.
证明:连结BD、CE,则
在△BCD和△CDE中
∵BC=CD
∠BCD=∠CDE
CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证对角线相等.
探究新知
6. 正六边形ABCDEF外切于⊙O,⊙O的半径为R,则该正六边形的周长和面积各是多少?
A
B
C
D
E
F
O
M
R
探究新知
7. 已知圆内接正 n 边形的边长为 a, 求同圆外切正 n 边形的边长b为多少? (用三角函数表示).
●
A
B
C
D
O
E
探究新知
8. 正六边形ABCDEF的边长是a,分别以C、F为圆心,a为半径作弧,则图中阴影部分的周长是_____.
A
B
C
D
E
F
⌒
⌒
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
正多边形
概念
计算
画法
应用
正多边形与圆的关系
正多边形的中心、半径、边心距、中心角
正多边形的对称性、相似性
半径、边心距、中心角的计算
边长、面积的计算
量角器等分圆周画正多边形
尺规作正方形、正六边形等
圆的周长、弧长及组合图形周长的计算
圆面积、扇形面积及组合图形面积的计算
课程:数学
《正多边形和圆》
人教版
九年级上册 第8课时
第 24 章 圆
教学目标
1
2
3
知识与技能
使学生理解正多边形概念,了解依次连结圆的n等分点所得的多边形是正多边形;过圆的n等分点作圆的切线,以相邻切线的交点为顶点的多边形是正多边形。
过程与方法
通过正多边形定义教学培养学生归纳能力:通过正多边形与圆关系定理的教学培养学生观察、猜想、推理、迁移能力
情感态度和价值观
向学生渗透“特殊——一般”再“一般——特殊”的唯物辩证法思想。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
正多边形
各边相等,各角也相等的多边形.
几种常见的正多边形
02
PART TWO
探究新知
Explore new knowledge
探究新知
各边相等,各角也相等的多边形叫做正多边形
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
三条边相等三个角相等(60度)。
四条边相等四个角相等(900)
正三角形
正方形
一 .正多边形定义
探究新知
正多边形的性质
60°
正n边形内角和:
(n-2)180°
108°
每条边都相等
每个角都相等
135°
探究新知
轴对称图形,
一个正n边形共有n条对称轴,
每条对称轴都通过n边形的中心.
正多边形的性质
正五边形
正八边形
正三边形
什么叫中心?
探究新知
边数是偶数的正多边形
是中心对称图形,
它的中心就是对称中心.
正八边形
正六边形
正多边形的性质
探究新知
菱形是正多边形吗?矩形是正多边形吗?
小练习
×
×
菱形的四个角不相等.
矩形的四条边不相等.
探究新知
C
A
B
D
E
正多边形和圆的关系非常密切,把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
探究新知
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
证明:∵AB=BC=CD=DE=EA
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
∴∠1=∠2
同理∠2=∠3=∠4=∠5
又∵顶点A、B、C、D、E都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
⊙O是五边形ABCDE的外接圆.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
定理证明
探究新知
把圆分成 n(n≥3)等份:
依次连结各分点所得的多边形是这个圆的内接正多边形.
内接正多边形
探究新知
E
F
C
D
.
.
O
中心角
半径R
边心距
r
中心:
一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径.
正多边形的中心角:
正多边形的每一条边
所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
中心
正多边形及外接圆中的有关概念
探究新知
E
F
C
D
.
.
O
中心角
A
B
G
边心距OG把△AOB分成
2个全等的直角三角形.
设正多边形的边长为a,半径为R,它的周长为L = na.
R
a
正多边形的有关计算
探究新知
A
B
C
D
正多边形 外接圆
弦相等
多边形的边相等
多边形的角相等
圆周角相等
内接正多边形与外接圆的联系
探究新知
把正n边形的边数无限增多,
正多边形
……
就接近于圆.
圆
由圆怎样得到正多边形?
探究新知
把一个圆4等分,并依次连接这些点,得到正多边形吗
探究
正方形
探究新知
已知⊙O的半径为2cm,求作圆的内接正三角形
120 °
A
O
C
B
探究
①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
一题多解
量角器作图
探究新知
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
小练习
探究新知
你能用尺规作出正四边形、正八边形吗?
·
A
B
C
D
O
探究
尺规作图
作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
探究新知
你能用尺规作出正六边形、正三角形、正十二边形吗?
O
A
B
C
E
F
·
D
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
探究新知
有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
例题
探究新知
A
B
C
D
E
O
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接正五边形和外切正五边形.
小练习
探究新知
把圆分成 n(n≥3)等份:
经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正多边形.
外切正多边形
探究新知
又∵五边形PQRST的各边都与⊙O相切,
∴五边形PQRST的是O外切正五边形。
证明:连结OA、OB、OC,则:
∠OAB=∠OBA=∠OBC=∠OCB
∵TP、PQ、QR分别是以A、B、C
为切点的⊙O的切线
∴∠OAP=∠OBP=∠OBQ=∠OCQ
∴∠PAB=∠PBA=∠QBC=∠QCB
又∵AB=BC
∴AB=BC
∴△PAB与△QBC是全等的等腰三角形。
∴∠P=∠Q PQ=2PA
同理∠Q=∠R=∠S=∠T
QR=RS=ST=TP=2PA
⌒
⌒
A
B
C
D
E
P
Q
R
S
T
O
定理证明
PART THREE
课堂练习
class exercise
03
课堂练习
1. 正n边形的一个内角的度数是____________;
中心角是___________;正多边形的中心角与外角的
大小关系是________.
相等
2. O是正△ABC的中心,它是△ABC的________圆与________圆的圆心.
外接
内切
探究新知
3. OB叫正△ABC的________ ,它是正△ABC的________圆的半径.
4. OD叫作正△ABC的________ ,它是正△ABC的________ 圆的半径。
A
B
C
.O
D
半径
外接
边心距
内切
探究新知
A
B
C
D
E
5. 求证:正五边形的对角线相等.
证明:连结BD、CE,则
在△BCD和△CDE中
∵BC=CD
∠BCD=∠CDE
CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证对角线相等.
探究新知
6. 正六边形ABCDEF外切于⊙O,⊙O的半径为R,则该正六边形的周长和面积各是多少?
A
B
C
D
E
F
O
M
R
探究新知
7. 已知圆内接正 n 边形的边长为 a, 求同圆外切正 n 边形的边长b为多少? (用三角函数表示).
●
A
B
C
D
O
E
探究新知
8. 正六边形ABCDEF的边长是a,分别以C、F为圆心,a为半径作弧,则图中阴影部分的周长是_____.
A
B
C
D
E
F
⌒
⌒
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
正多边形
概念
计算
画法
应用
正多边形与圆的关系
正多边形的中心、半径、边心距、中心角
正多边形的对称性、相似性
半径、边心距、中心角的计算
边长、面积的计算
量角器等分圆周画正多边形
尺规作正方形、正六边形等
圆的周长、弧长及组合图形周长的计算
圆面积、扇形面积及组合图形面积的计算
同课章节目录
