2022—2023学年人教版数学九年级上册 24.4弧长和扇形面积 课件(共26张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册 24.4弧长和扇形面积 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 08:37:44 | ||
图片预览







文档简介
(共26张PPT)
课程:数学
《弧长和扇形面积》
人教版
九年级上册 第9课时
第 24 章 圆
教学目标
1
2
3
知识与技能
经历探索弧长计算公式的过程,培养学生的探索能力;了解弧长计算公式,并会应用弧长公式解决问题,提高学生的应用能力·
过程与方法
通过等分圆周的方法,体验弧长扇形面积公式的推导过程,培养学生抽象、理解、概括、归纳能力和迁移能力·
情感态度和价值观
通过图形的转通过对弧长和扇形面积公式的推导,理解整体和局部的关系化,体会转化在数学解题中的妙用.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
弧
圆上任意两点间的部分叫做圆弧,简称弧
02
PART TWO
探究新知
Explore new knowledge
探究新知
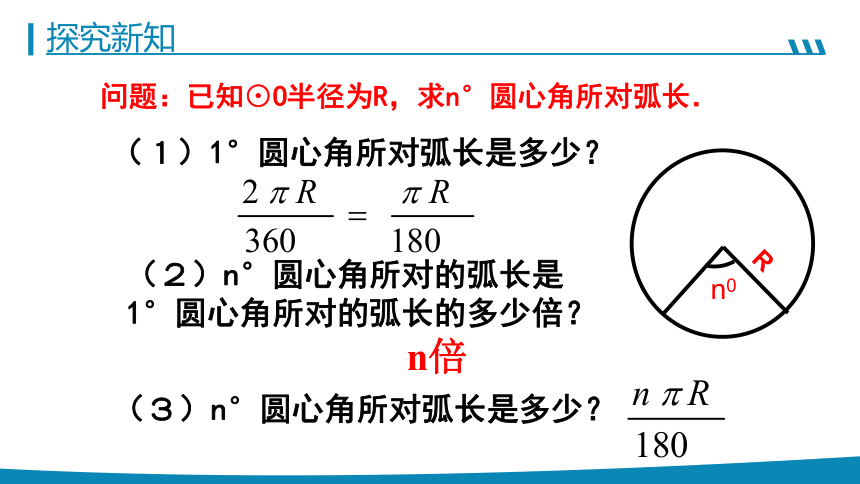
问题:已知⊙O半径为R,求n°圆心角所对弧长.
(1)1°圆心角所对弧长是多少?
(2)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
(3)n°圆心角所对弧长是多少?
n0
R
探究新知
若设⊙O半径为R, n°的圆心角所对的弧长为L,则
(1)在应用弧长公式L , 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
注意:
弧长公式
探究新知
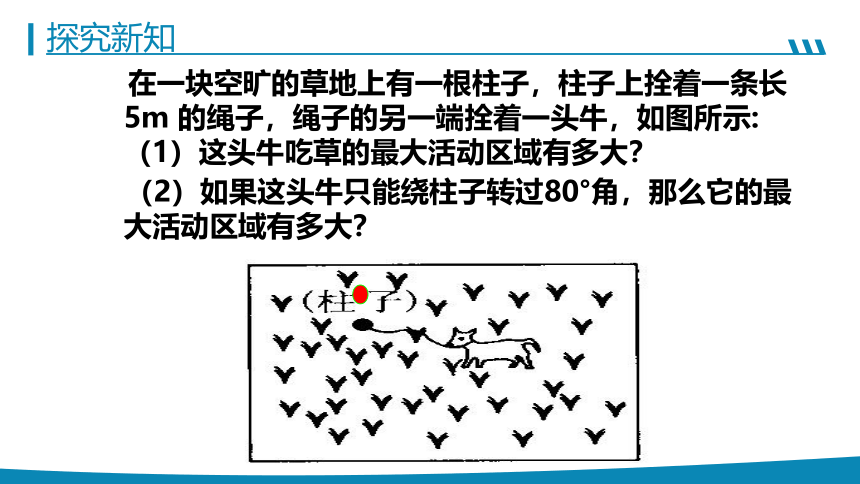
在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?
探究新知
扇形的定义
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
A
B
O
图中阴影部分的图形叫什么呢?
扇形
C
探究新知
已知⊙O半径为R,求圆心角n°的扇形的面积
(1)圆面积可以看作是多少度的圆心角所对的扇形的面积?
360°
(2)圆心角为1°的扇形的面积是多少
(3)圆心角为n°的扇形的面积是圆心角为
1°的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少
探究新知
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形=
注意:
在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.
n表示1°圆心角的倍数,它是不带单位的
探究新知
比较弧长公式与扇形面积公式
l 弧
= πR
180
n
S扇形
360
n
= πR2
在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l 和S之间也有一定的关系,你能猜得出吗
探究新知
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,
可得弧AB 的长
l (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
探究新知
例:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m2)。
0
B
A
C
D
弓形的面积 = S扇- S⊿
提示:要求的面积,可以通过哪些图形面积的和或差求得
探究新知
解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:
∴OD=OC-DC=0.6-0.3=0.3
∴∠AOD=60°, ∠ AOB=120°
在Rt△ OAD中,∵OD=0.5OA
0.6
0.3
0
B
A
C
D
∴∠ OAD=30°
有水部分的面积为=
探究新知
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
探究新知
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
规律提升
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
PART THREE
课堂练习
class exercise
03
课堂练习
2、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为_______
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇=_ .
112π
探究新知
3、某扇形的周长是28cm,面积为49平方厘米,则这个扇形的半径是______
4、如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则S阴影=_______
7cm
2.5π-4
探究新知
5、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积,S扇= .
6、一扇形的弧长是 ,面积为
那么扇形的圆心角为 .
150度
探究新知
B
C
A
7、⊙A, ⊙B, ⊙C 两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少 弧长的和为多少
解:∵三个扇形的圆心角是三角形的三个内角
∴三个扇形的圆心角之和是180°
∴三个扇形的面积相当于半径是1cm,圆
心角为180°的圆
∴三个扇形的面积之和是
S=
S=cm2
∴
∴弧长之和是
l=
l=πcm
∴
探究新知
7.如图,正三角形ABC的边长为a,分别以A、B、 C 为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积.
A
B
C
F
E
D
解:连接AD,则
垂足为D
根据勾股定理,得
AD⊥BC
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
2.扇形面积公式与弧长公式与圆的知识的联系:
S扇形= S圆
360
n
l弧= C圆
360
n
1.扇形的弧长和面积大小与哪些因素有关?
(2)与半径的长短有关
(1)与圆心角的大小有关
课程:数学
《弧长和扇形面积》
人教版
九年级上册 第9课时
第 24 章 圆
教学目标
1
2
3
知识与技能
经历探索弧长计算公式的过程,培养学生的探索能力;了解弧长计算公式,并会应用弧长公式解决问题,提高学生的应用能力·
过程与方法
通过等分圆周的方法,体验弧长扇形面积公式的推导过程,培养学生抽象、理解、概括、归纳能力和迁移能力·
情感态度和价值观
通过图形的转通过对弧长和扇形面积公式的推导,理解整体和局部的关系化,体会转化在数学解题中的妙用.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
弧
圆上任意两点间的部分叫做圆弧,简称弧
02
PART TWO
探究新知
Explore new knowledge
探究新知
问题:已知⊙O半径为R,求n°圆心角所对弧长.
(1)1°圆心角所对弧长是多少?
(2)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
(3)n°圆心角所对弧长是多少?
n0
R
探究新知
若设⊙O半径为R, n°的圆心角所对的弧长为L,则
(1)在应用弧长公式L , 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
注意:
弧长公式
探究新知
在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?
探究新知
扇形的定义
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
A
B
O
图中阴影部分的图形叫什么呢?
扇形
C
探究新知
已知⊙O半径为R,求圆心角n°的扇形的面积
(1)圆面积可以看作是多少度的圆心角所对的扇形的面积?
360°
(2)圆心角为1°的扇形的面积是多少
(3)圆心角为n°的扇形的面积是圆心角为
1°的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少
探究新知
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形=
注意:
在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.
n表示1°圆心角的倍数,它是不带单位的
探究新知
比较弧长公式与扇形面积公式
l 弧
= πR
180
n
S扇形
360
n
= πR2
在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l 和S之间也有一定的关系,你能猜得出吗
探究新知
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,
可得弧AB 的长
l (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
探究新知
例:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m2)。
0
B
A
C
D
弓形的面积 = S扇- S⊿
提示:要求的面积,可以通过哪些图形面积的和或差求得
探究新知
解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:
∴OD=OC-DC=0.6-0.3=0.3
∴∠AOD=60°, ∠ AOB=120°
在Rt△ OAD中,∵OD=0.5OA
0.6
0.3
0
B
A
C
D
∴∠ OAD=30°
有水部分的面积为=
探究新知
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
探究新知
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
规律提升
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
PART THREE
课堂练习
class exercise
03
课堂练习
2、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为_______
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇=_ .
112π
探究新知
3、某扇形的周长是28cm,面积为49平方厘米,则这个扇形的半径是______
4、如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则S阴影=_______
7cm
2.5π-4
探究新知
5、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积,S扇= .
6、一扇形的弧长是 ,面积为
那么扇形的圆心角为 .
150度
探究新知
B
C
A
7、⊙A, ⊙B, ⊙C 两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少 弧长的和为多少
解:∵三个扇形的圆心角是三角形的三个内角
∴三个扇形的圆心角之和是180°
∴三个扇形的面积相当于半径是1cm,圆
心角为180°的圆
∴三个扇形的面积之和是
S=
S=cm2
∴
∴弧长之和是
l=
l=πcm
∴
探究新知
7.如图,正三角形ABC的边长为a,分别以A、B、 C 为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积.
A
B
C
F
E
D
解:连接AD,则
垂足为D
根据勾股定理,得
AD⊥BC
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
2.扇形面积公式与弧长公式与圆的知识的联系:
S扇形= S圆
360
n
l弧= C圆
360
n
1.扇形的弧长和面积大小与哪些因素有关?
(2)与半径的长短有关
(1)与圆心角的大小有关
同课章节目录
