2021-2022学年人教版九年级上册数学 21.3实际问题与一元二次方程—传染问题 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版九年级上册数学 21.3实际问题与一元二次方程—传染问题 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 08:48:32 | ||
图片预览








文档简介
(共21张PPT)
课程:数学
《实际问题与一元二次方程
一传播问题》
人教版
九年级上册 第10课时
第 21 章 一元二次方程
教学目标
1
2
3
知识与技能
1.能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型.
2.能根据具体问题的实际意义,检验结果是否合理.
过程与方法
通过解决封面设计与草坪规划的实际问题,学会将实际应用问题转化为数学问题,体验解决问题策略的多样性,发展实践应用意识.
情感态度和价值观
通过用一元二次方程解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣,了解数学对促进社会进步和发展人类理性精神的作用.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
02
PART TWO
探究新知
Explore new knowledge
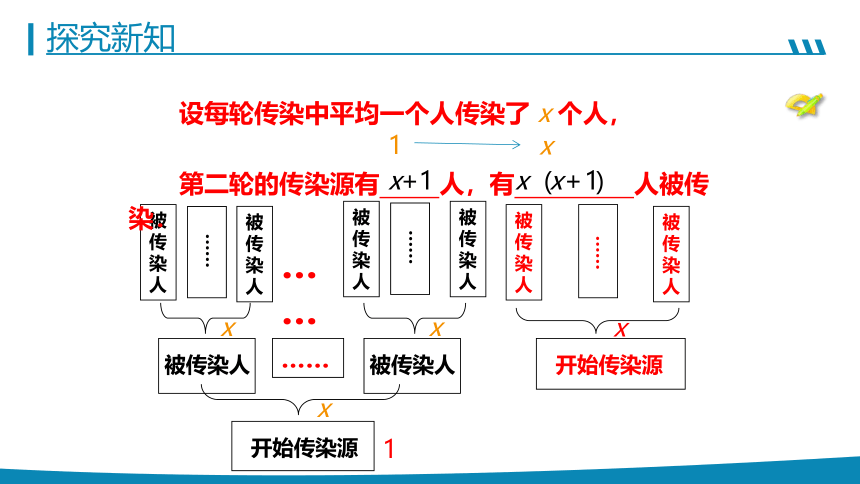
探究新知
探究 有一个人患了新冠,经过两轮传染后共有 121个人患了新冠,每轮传染中平均一个人传染了几个
人?
(2)每一轮的传染源和传染之后的患新冠人数是
多少?
(1)本题中的数量关系是什么?
分析:
探究新知
……
被传染人
被传染人
……
被传染人
被传染人
……
……
x
x
开始传染源
1
被传染人
被传染人
x
设每轮传染中平均一个人传染了 x 个人,
开始传染源
被传染人
被传染人
……
x
第二轮的传染源有 人,有 人被传染.
1
x
x+1
x x + 1
( )
探究新知
传染源数、第一轮被传染数和第二轮被传染数的总和是 121 个人.
探究 有一个人患了新冠,经过两轮传染后共有 121个人患了新冠,每轮传染中平均一个人传染了几个
人?
(3)如何理解经过两轮传染后共有 121 个人患了
新冠?
分析:
探究新知
解:设每轮传染中平均一个人传染了 x 个人.
x1 =______,x2 =______
答:平均一个人传染了 10 个人.
10
(不合题意,舍去) .
-12
探究 有一个人患了新冠,经过两轮传染后共有 121个人患了新冠,每轮传染中平均一个人传染了几个
人?
(4)如何利用已知数量关系列出方程,并解方程
得出结论?
分析:
1 + x + x 1 + x = 121
( )
探究新知
(5)如果按照这样的传染速度,三轮传染后有多
少个人患新冠?
121+121×10 = 1 331(人)
(6)通过对这个问题的探究,你对类似的传播问
题中的数量关系有新的认识吗?
探究新知
有关“动点”的运动问题”
1)关键—— 以静代动
把动的点进行转换,变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;
由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.
3)常找的数量关系——
面积,勾股定理等;
探究新知
例1 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后⊿ PBQ的面积等于8cm2?
解:设x秒后⊿ PBQ的面积等于8cm2
根据题意,得
整理,得
解这个方程,得
所以2秒或4秒后⊿ PBQ的面积等于8cm2
探究新知
例2:等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2
PART THREE
课堂练习
class exercise
03
课堂练习
1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为 .
B
探究新知
3:△ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P是AB上的一动点(不与A,B重合),且AP=x,过点P作直线l与AB垂直.
i)设△ ABC位于直线l左侧部分的面积为S,写出S与x之间的函数关系式;
ii)当x为何值时,直线l平分⊿ ABC的面积
探究新知
例4:客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮,两船若同时起航,并同时到达折线A-B-C上的某点E处,已知AB=BC=200海里, ∠ABC=90°,客轮速度是货轮速度的2倍.
(1)选择:两船相遇之处E点( )
A.在线段AB上;
B.在线段BC上;
C.可以在线段AB上,也可以在线段BC上;
探究新知
ii)求货轮从出发到两船相遇共航行了多少海里 (结果保留根号)
解:设货轮从出发到两船相遇共航行了x海里,过D作DF⊥ CB,交BD于F,则DE=x,AB+BE=2x,DF=100,EF=300-2x
在Rt⊿DEF 中,
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
1、平均增长(降低)率公式
2、注意:
(1)1与x的位置不要调换
(2)解这类问题列出的方程一般
用 直接开平方法
课程:数学
《实际问题与一元二次方程
一传播问题》
人教版
九年级上册 第10课时
第 21 章 一元二次方程
教学目标
1
2
3
知识与技能
1.能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型.
2.能根据具体问题的实际意义,检验结果是否合理.
过程与方法
通过解决封面设计与草坪规划的实际问题,学会将实际应用问题转化为数学问题,体验解决问题策略的多样性,发展实践应用意识.
情感态度和价值观
通过用一元二次方程解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣,了解数学对促进社会进步和发展人类理性精神的作用.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
02
PART TWO
探究新知
Explore new knowledge
探究新知
探究 有一个人患了新冠,经过两轮传染后共有 121个人患了新冠,每轮传染中平均一个人传染了几个
人?
(2)每一轮的传染源和传染之后的患新冠人数是
多少?
(1)本题中的数量关系是什么?
分析:
探究新知
……
被传染人
被传染人
……
被传染人
被传染人
……
……
x
x
开始传染源
1
被传染人
被传染人
x
设每轮传染中平均一个人传染了 x 个人,
开始传染源
被传染人
被传染人
……
x
第二轮的传染源有 人,有 人被传染.
1
x
x+1
x x + 1
( )
探究新知
传染源数、第一轮被传染数和第二轮被传染数的总和是 121 个人.
探究 有一个人患了新冠,经过两轮传染后共有 121个人患了新冠,每轮传染中平均一个人传染了几个
人?
(3)如何理解经过两轮传染后共有 121 个人患了
新冠?
分析:
探究新知
解:设每轮传染中平均一个人传染了 x 个人.
x1 =______,x2 =______
答:平均一个人传染了 10 个人.
10
(不合题意,舍去) .
-12
探究 有一个人患了新冠,经过两轮传染后共有 121个人患了新冠,每轮传染中平均一个人传染了几个
人?
(4)如何利用已知数量关系列出方程,并解方程
得出结论?
分析:
1 + x + x 1 + x = 121
( )
探究新知
(5)如果按照这样的传染速度,三轮传染后有多
少个人患新冠?
121+121×10 = 1 331(人)
(6)通过对这个问题的探究,你对类似的传播问
题中的数量关系有新的认识吗?
探究新知
有关“动点”的运动问题”
1)关键—— 以静代动
把动的点进行转换,变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;
由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.
3)常找的数量关系——
面积,勾股定理等;
探究新知
例1 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后⊿ PBQ的面积等于8cm2?
解:设x秒后⊿ PBQ的面积等于8cm2
根据题意,得
整理,得
解这个方程,得
所以2秒或4秒后⊿ PBQ的面积等于8cm2
探究新知
例2:等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2
PART THREE
课堂练习
class exercise
03
课堂练习
1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为 .
B
探究新知
3:△ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P是AB上的一动点(不与A,B重合),且AP=x,过点P作直线l与AB垂直.
i)设△ ABC位于直线l左侧部分的面积为S,写出S与x之间的函数关系式;
ii)当x为何值时,直线l平分⊿ ABC的面积
探究新知
例4:客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮,两船若同时起航,并同时到达折线A-B-C上的某点E处,已知AB=BC=200海里, ∠ABC=90°,客轮速度是货轮速度的2倍.
(1)选择:两船相遇之处E点( )
A.在线段AB上;
B.在线段BC上;
C.可以在线段AB上,也可以在线段BC上;
探究新知
ii)求货轮从出发到两船相遇共航行了多少海里 (结果保留根号)
解:设货轮从出发到两船相遇共航行了x海里,过D作DF⊥ CB,交BD于F,则DE=x,AB+BE=2x,DF=100,EF=300-2x
在Rt⊿DEF 中,
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
1、平均增长(降低)率公式
2、注意:
(1)1与x的位置不要调换
(2)解这类问题列出的方程一般
用 直接开平方法
同课章节目录
