2022-2023学年人教版数学九年级上册21.1 一元二次方程(第2课时)课件 (共25张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册21.1 一元二次方程(第2课时)课件 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 08:55:18 | ||
图片预览







文档简介
(共25张PPT)
《一元二次方程(2)》
人教版
九年级上册 第2课时
课程:九年级数学
第 21章 一元二次方程
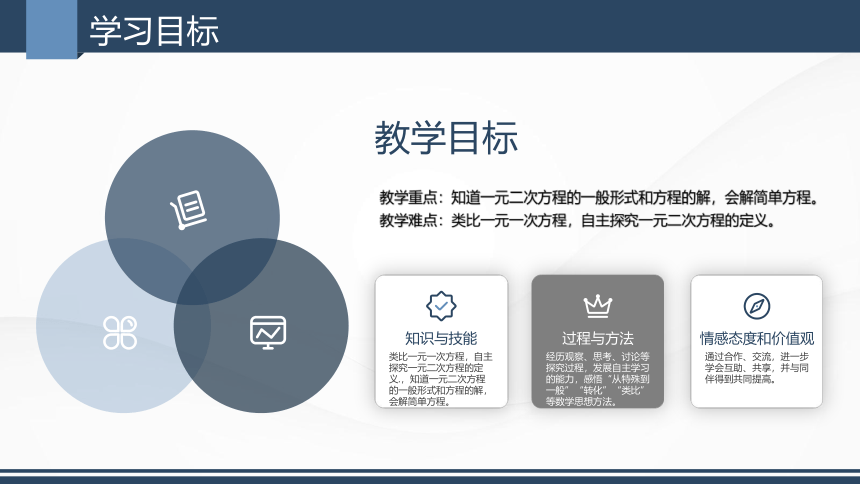
学习目标
教学目标
教学重点:知道一元二次方程的一般形式和方程的解,会解简单方程。教学难点:类比一元一次方程,自主探究一元二次方程的定义。
知识与技能
类比一元一次方程,自主探究一元二次方程的定义.,知道一元二次方程的一般形式和方程的解,会解简单方程。
过程与方法
情感态度和价值观
经历观察、思考、讨论等探究过程,发展自主学习的能力,感悟“从特殊到一般”“转化”“类比”等数学思想方法。
通过合作、交流,进一步学会互助、共享,并与同伴得到共同提高。
目录
CONTENTS
01情景导入
Scenario importt
03典型例题
Typical examples
02探究新知
Explore new knowledge
04课后小结
Class summary
情景导入
01
Scenario importt
情景导入
01
1.一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
复习巩固
探究新知
02
Explore new knowledge
探究新知
02
上一节我们认识了一元二次方程,接下来我们就要探求一元二次方程的解.
方程解的定义是怎样的呢
能使方程左右两边相等的未知数的值就叫方程的解
探 究
探究新知
02
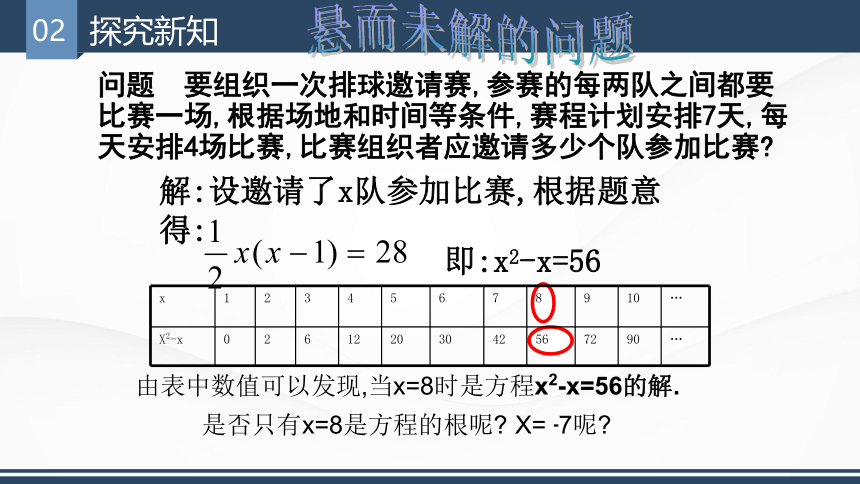
悬而未解的问题
问题 要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
解:设邀请了x队参加比赛,根据题意得:
即:x2-x=56
x 1 2 3 4 5 6 7 8 9 10 …
X2-x 0 2 6 12 20 30 42 56 72 90 …
由表中数值可以发现,当x=8时是方程x2-x=56的解.
是否只有x=8是方程的根呢
X= -7呢
探究新知
02
思考:
你能否说出下列方程的解
1)
2)
3)
一元二次方程的根的情况与一元一次方程有什么不同吗
探究新知
02
练习:
1)下面哪些数是方程 的根
-4 -3 -2 -1 0 1 2 3 4
2)你能写出方程 的根吗
即:平方后是它本身的数是哪些
0或1
探究新知
02
例题讲解
A.1 B.-1 C.1或-1 D.0
B
探究新知
02
例题讲解
一元二次方程
探究新知
02
探究新知
02
例题讲解
例题讲解
方程
一元二次方程
探究新知
02
探究新知
02
例题讲解
例题讲解
探究新知
02
典型例题
03
Typical examples
典型例题
03
1.已知方程x2+mx-12=0的一个根是x=-2,求m的值。
3.方程(x2-1)(2x+5)=0的解为____________。
2.方程(x-1)(x+3)(x -2)=0的解为____________.
4.已知m是方程x2+x-2009=0的一个根,
求m2+m的值为 。
m=-4
x1=1,x2=-3,x3=2
x1=1,x2=-1,x3=2.5
2009
典型例题
03
5.方程x2-2007x-2008=0的解为( )
1;2 B. 2;2008
C. -1;2008 D. 1;-2008
6. 已知6和-7是某一个方程的两个根,则该方程可以是( )
(x-7)(x+6)=0 B. (x+7)(x+6)=0
C. x2-x+42=0 D. x2+x-42=0
c
D
典型例题
03
X=-1
X=1
典型例题
03
x 3.23 3.24 3.25 3.26
-0.06 -0.02 0.03 0.07
A 3<x <3.23
C 3.24<x <3.25
D 3.25<x <3.26
B 3.23<x <3.24
C
X=2
典型例题
03
提高题:
若方程x2a+b-2xa-b+3=0是关于x的一元二次方程,则a、b的值各是多少?
课后小结
04
Class summary
课后小结
04
这节课你们都学会了哪些知识?
1.一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
3、模仿一元二次方程的定义你能对一元三次
方程下个定义吗?请你试试看!
《一元二次方程(2)》
人教版
九年级上册 第2课时
课程:九年级数学
第 21章 一元二次方程
学习目标
教学目标
教学重点:知道一元二次方程的一般形式和方程的解,会解简单方程。教学难点:类比一元一次方程,自主探究一元二次方程的定义。
知识与技能
类比一元一次方程,自主探究一元二次方程的定义.,知道一元二次方程的一般形式和方程的解,会解简单方程。
过程与方法
情感态度和价值观
经历观察、思考、讨论等探究过程,发展自主学习的能力,感悟“从特殊到一般”“转化”“类比”等数学思想方法。
通过合作、交流,进一步学会互助、共享,并与同伴得到共同提高。
目录
CONTENTS
01情景导入
Scenario importt
03典型例题
Typical examples
02探究新知
Explore new knowledge
04课后小结
Class summary
情景导入
01
Scenario importt
情景导入
01
1.一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
复习巩固
探究新知
02
Explore new knowledge
探究新知
02
上一节我们认识了一元二次方程,接下来我们就要探求一元二次方程的解.
方程解的定义是怎样的呢
能使方程左右两边相等的未知数的值就叫方程的解
探 究
探究新知
02
悬而未解的问题
问题 要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
解:设邀请了x队参加比赛,根据题意得:
即:x2-x=56
x 1 2 3 4 5 6 7 8 9 10 …
X2-x 0 2 6 12 20 30 42 56 72 90 …
由表中数值可以发现,当x=8时是方程x2-x=56的解.
是否只有x=8是方程的根呢
X= -7呢
探究新知
02
思考:
你能否说出下列方程的解
1)
2)
3)
一元二次方程的根的情况与一元一次方程有什么不同吗
探究新知
02
练习:
1)下面哪些数是方程 的根
-4 -3 -2 -1 0 1 2 3 4
2)你能写出方程 的根吗
即:平方后是它本身的数是哪些
0或1
探究新知
02
例题讲解
A.1 B.-1 C.1或-1 D.0
B
探究新知
02
例题讲解
一元二次方程
探究新知
02
探究新知
02
例题讲解
例题讲解
方程
一元二次方程
探究新知
02
探究新知
02
例题讲解
例题讲解
探究新知
02
典型例题
03
Typical examples
典型例题
03
1.已知方程x2+mx-12=0的一个根是x=-2,求m的值。
3.方程(x2-1)(2x+5)=0的解为____________。
2.方程(x-1)(x+3)(x -2)=0的解为____________.
4.已知m是方程x2+x-2009=0的一个根,
求m2+m的值为 。
m=-4
x1=1,x2=-3,x3=2
x1=1,x2=-1,x3=2.5
2009
典型例题
03
5.方程x2-2007x-2008=0的解为( )
1;2 B. 2;2008
C. -1;2008 D. 1;-2008
6. 已知6和-7是某一个方程的两个根,则该方程可以是( )
(x-7)(x+6)=0 B. (x+7)(x+6)=0
C. x2-x+42=0 D. x2+x-42=0
c
D
典型例题
03
X=-1
X=1
典型例题
03
x 3.23 3.24 3.25 3.26
-0.06 -0.02 0.03 0.07
A 3<x <3.23
C 3.24<x <3.25
D 3.25<x <3.26
B 3.23<x <3.24
C
X=2
典型例题
03
提高题:
若方程x2a+b-2xa-b+3=0是关于x的一元二次方程,则a、b的值各是多少?
课后小结
04
Class summary
课后小结
04
这节课你们都学会了哪些知识?
1.一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
3、模仿一元二次方程的定义你能对一元三次
方程下个定义吗?请你试试看!
同课章节目录
