2022-2023学年人教版数学九年级上册第 21.2.1直接开平方法解一元二次方程 课件 (共27张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册第 21.2.1直接开平方法解一元二次方程 课件 (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 08:57:31 | ||
图片预览








文档简介
(共27张PPT)
课 程:数 学
《直接开平方法解一元二次方程》
人教版
九年级上册 第3课时
第 21 章 一元二次方程
教学目标
1、使学生知道形如x2=a(a≥0)的一元二次方程可以用直接开平方法求解;
2、使学生知道直接开平方法求一元二次方程的解的依据是数的开平方;
3、使学生能够熟练而准确的运用直接开平方法求一元二次方程的解。
知识与技能
在学习与探究中使学生体会“化归”、“换元”与“分类讨论”的数学思想及运用类比进行学习的方法。
过程与方法
使学生在学习中体会愉悦与成功感,感受数学学习的价值。
情感态度和价值观
新课导入
New class introduction
01
探究新知
Explore new knowledge
02
课堂练习
class exercise
03
课堂小结
Class summary
04
目/录
CONTENTS
新课导入
01
New class introduction
新课导入
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
1、一元二次方程的概念
2、一元二次方程的一般形式
新课导入
1.什么叫做平方根
如果一个数的平方等于a,那么这个数就叫
做a的平方根.
若x2=a,则x=
如:9的平方根是______,
±3
的平方根是______
2.平方根有哪些性质?
(1)一个正数有两个平方根,这两个平方根
互为相反数的;
(2)零的平方根是零;
(3)负数没有平方根.
即x= 或x=
探究新知
02
Explore new knowledge
探究新知
问题1 在设计人体雕像时,使雕像的上部(腰以
上)与下部(腰以下)的高度比,等于下部与全部(全
身)的高度比,可以增加视觉美感.按此比例,如果雕
像的高为 2 m,那么它的下部应设计为多高?
解:设雕像的下部高为 x m,
据题意,列方程得
整理得 x 2 + 2x - 4 = 0.
A
C
B
x 2 = 2 2 - x ,
( )
探究新知
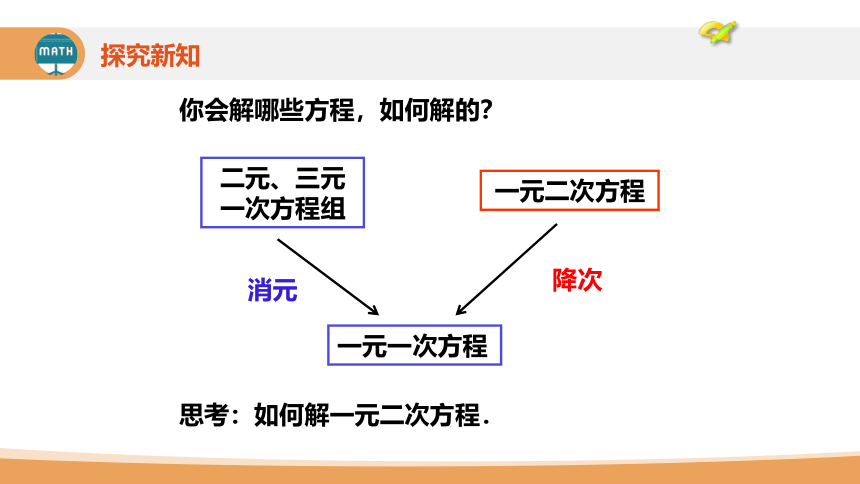
你会解哪些方程,如何解的?
二元、三元一次方程组
一元一次方程
一元二次方程
消元
降次
思考:如何解一元二次方程.
探究新知
问题2 解方程 x 2 = 25,依据是什么?
解得 x 1 = 5,x 2 = - 5.
平方根的意义
请解下列方程: x 2 = 3,2x 2 - 8=0,x 2 = 0,x 2 = - 2…
这些方程有什么共同的特征?
结构特征:方程可化成 x 2 = p 的形式,
平方根的意义
降次
(当 p≥0 时)
问题3 解方程:(x + 3)= 5.
2
探究新知
问题4 怎样解方程 x 2 + 6x + 4 = 0 ①?
x 2 + 6x + 9 = 5 ②
(x + 3)= 5
2
探究新知
试一试:与方程 x2 + 6x + 9 = 5 ② 比较,
怎样解方程 x2 + 6x + 4 = 0 ① ?
怎样把方程①化成方程②的形式呢?
怎样保证变形的正确性呢?
即
由此可得…
解:
左边写成平方形式
移项
x2 + 6x = -4 ③
两边加 9
= -4 + 9
x2 + 6x + 9
(x + 3)= 5
2
探究新知
回顾解方程过程:
两边加 9,左边
配成完全平方式
移项
左边写成完全
平方形式
降次
解一次方程
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
,
(x + 3)= 5
2
探究新知
想一想:以上解法中,为什么在方程③两边加 9?
加其他数可以吗?如果不可以,说明理由.
两边加 9
一般地,当二次项系数为 1 时,二次式加上一次项系数一半的平方,二次式就可以写成完全平方的形式.
x2 + 6x = -4 ③
x2 + 6x + 9 = -4 + 9
(x + 3)= 5
2
9,即 2 = 3 2 = 9
( )
探究新知
议一议:结合方程①的解答过程,说出解一般二次
项系数为 1 的一元二次方程的基本思路是什么?具体步
骤是什么?
配成完全平方形式
通过 来解一元二次方程的方法,
叫做配方法.
配方
具体步骤:
(1)移项;
(2)在方程两边都加上一次项系数一半的平方.
探究新知
平方根的意义
降次
(当 p≥0 时)
问题5 通过解方程 x 2 + 6x + 4=0 ,请归纳这类方程是怎样解的?
结构特征:方程可化成 的形式,
(x + n)= p
2
探究新知
(2)配方法解一元二次方程的一般步骤有哪些
(1)用配方法解一元二次方程的基本思路是什么?
把方程配方为 的形式,运用开平方法,
降次求解.
(x + n)= p
2
探究新知
解一元二次方程的一般步骤:
两边加 9,左边
配成完全平方式
移项
左边写成完全
平方形式
降次
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
(x + 3)= 5
2
解一次方程
,
课堂练习
03
class exercise
课堂练习
;x2=
(D)(2x+3)2=25,解方程,得2x+3=±5,x1= 1;x2=-4
1、下列解方程的过程中,正确的是( )
(A)x2=-2,解方程,得x=±
(B)(x-2)2=4,解方程,得x-2=2,x=4
(C)4(x-1)2=9,解方程,得4(x-1)= ±3, x1=
D
课堂练习
A.n=0 B.m、n异号
C.n是m的整数倍 D.m、n同号
2、已知一元二次方程mx2+n=0(m≠0),若方
程可以用直接开平方法求解,且有两个
实数根,则m、n必须满足的条件是( )
B
课堂练习
3、小试身手 :
1) x2=2 ( )
2) p2 - 49=0 ( )
3) 6 x2=3 ( )
4) (5x+9)2+16=0 ( )
5) 121-(y+3) 2 =0 ( )
×
√
√
√
√
课堂练习
4、解下列方程
(1)x2-1.21=0 (2)4x2-1=0
解:(1)移项,得x2=1.21
∵x是1.21的平方根
∴x=±1.1
即 x1=1.1,x2=-1.1
(2)移项,得4x2=1
两边都除以4,得
∵x是 的平方根
∴x=
即x1= ,x2=
x2=
课堂练习
即x1=-1+
,x2=-1-
5、解下列方程:
⑴(x+1)2= 2
分析:只要将(x+1)看成是一个整体,
就可以运用直接开平方法求解;
解:(1)∵x+1是2的平方根
∴x+1=
∴x+1=
或x+1=
课堂练习
⑵ (x-1)2-4 = 0
∴ x1=3,x2=-1
解:移项,得(x-1)2=4
∵x-1是4的平方根
∴x-1=±2
即x-1=+2 或x-1=-2
⑶ 12(3-2x)2-3 = 0
∴x1= ,
x2=
解:移项,得12(3-2x)2=3
两边都除以12,得(3-2x)2=0.25
∵3-2x是0.25的平方根
∴3-2x=±0.5
即3-2x=0.5或3-2x=-0.5
课堂小结
04
Class summary
课堂小结
首先将一元二次方程化为左边是含有未知数的一个完全平方式,右边是非负数的形式,然后用平方根的概念求解 .
归纳
1.能用直接开平方法解的一元二次方程有什么特点?
如果一个一元二次方程具有x2=a(a≥0)或 (ax+h)2= k(k≥0)的形式,那么就可以用直接开平方法求解.
2.用直接开平方法解一元二次方程的一般步骤是什么?
3.任意一个一元二次方程都能用直接开平方法求解吗?请举例说明.
课 程:数 学
《直接开平方法解一元二次方程》
人教版
九年级上册 第3课时
第 21 章 一元二次方程
教学目标
1、使学生知道形如x2=a(a≥0)的一元二次方程可以用直接开平方法求解;
2、使学生知道直接开平方法求一元二次方程的解的依据是数的开平方;
3、使学生能够熟练而准确的运用直接开平方法求一元二次方程的解。
知识与技能
在学习与探究中使学生体会“化归”、“换元”与“分类讨论”的数学思想及运用类比进行学习的方法。
过程与方法
使学生在学习中体会愉悦与成功感,感受数学学习的价值。
情感态度和价值观
新课导入
New class introduction
01
探究新知
Explore new knowledge
02
课堂练习
class exercise
03
课堂小结
Class summary
04
目/录
CONTENTS
新课导入
01
New class introduction
新课导入
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
1、一元二次方程的概念
2、一元二次方程的一般形式
新课导入
1.什么叫做平方根
如果一个数的平方等于a,那么这个数就叫
做a的平方根.
若x2=a,则x=
如:9的平方根是______,
±3
的平方根是______
2.平方根有哪些性质?
(1)一个正数有两个平方根,这两个平方根
互为相反数的;
(2)零的平方根是零;
(3)负数没有平方根.
即x= 或x=
探究新知
02
Explore new knowledge
探究新知
问题1 在设计人体雕像时,使雕像的上部(腰以
上)与下部(腰以下)的高度比,等于下部与全部(全
身)的高度比,可以增加视觉美感.按此比例,如果雕
像的高为 2 m,那么它的下部应设计为多高?
解:设雕像的下部高为 x m,
据题意,列方程得
整理得 x 2 + 2x - 4 = 0.
A
C
B
x 2 = 2 2 - x ,
( )
探究新知
你会解哪些方程,如何解的?
二元、三元一次方程组
一元一次方程
一元二次方程
消元
降次
思考:如何解一元二次方程.
探究新知
问题2 解方程 x 2 = 25,依据是什么?
解得 x 1 = 5,x 2 = - 5.
平方根的意义
请解下列方程: x 2 = 3,2x 2 - 8=0,x 2 = 0,x 2 = - 2…
这些方程有什么共同的特征?
结构特征:方程可化成 x 2 = p 的形式,
平方根的意义
降次
(当 p≥0 时)
问题3 解方程:(x + 3)= 5.
2
探究新知
问题4 怎样解方程 x 2 + 6x + 4 = 0 ①?
x 2 + 6x + 9 = 5 ②
(x + 3)= 5
2
探究新知
试一试:与方程 x2 + 6x + 9 = 5 ② 比较,
怎样解方程 x2 + 6x + 4 = 0 ① ?
怎样把方程①化成方程②的形式呢?
怎样保证变形的正确性呢?
即
由此可得…
解:
左边写成平方形式
移项
x2 + 6x = -4 ③
两边加 9
= -4 + 9
x2 + 6x + 9
(x + 3)= 5
2
探究新知
回顾解方程过程:
两边加 9,左边
配成完全平方式
移项
左边写成完全
平方形式
降次
解一次方程
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
,
(x + 3)= 5
2
探究新知
想一想:以上解法中,为什么在方程③两边加 9?
加其他数可以吗?如果不可以,说明理由.
两边加 9
一般地,当二次项系数为 1 时,二次式加上一次项系数一半的平方,二次式就可以写成完全平方的形式.
x2 + 6x = -4 ③
x2 + 6x + 9 = -4 + 9
(x + 3)= 5
2
9,即 2 = 3 2 = 9
( )
探究新知
议一议:结合方程①的解答过程,说出解一般二次
项系数为 1 的一元二次方程的基本思路是什么?具体步
骤是什么?
配成完全平方形式
通过 来解一元二次方程的方法,
叫做配方法.
配方
具体步骤:
(1)移项;
(2)在方程两边都加上一次项系数一半的平方.
探究新知
平方根的意义
降次
(当 p≥0 时)
问题5 通过解方程 x 2 + 6x + 4=0 ,请归纳这类方程是怎样解的?
结构特征:方程可化成 的形式,
(x + n)= p
2
探究新知
(2)配方法解一元二次方程的一般步骤有哪些
(1)用配方法解一元二次方程的基本思路是什么?
把方程配方为 的形式,运用开平方法,
降次求解.
(x + n)= p
2
探究新知
解一元二次方程的一般步骤:
两边加 9,左边
配成完全平方式
移项
左边写成完全
平方形式
降次
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
(x + 3)= 5
2
解一次方程
,
课堂练习
03
class exercise
课堂练习
;x2=
(D)(2x+3)2=25,解方程,得2x+3=±5,x1= 1;x2=-4
1、下列解方程的过程中,正确的是( )
(A)x2=-2,解方程,得x=±
(B)(x-2)2=4,解方程,得x-2=2,x=4
(C)4(x-1)2=9,解方程,得4(x-1)= ±3, x1=
D
课堂练习
A.n=0 B.m、n异号
C.n是m的整数倍 D.m、n同号
2、已知一元二次方程mx2+n=0(m≠0),若方
程可以用直接开平方法求解,且有两个
实数根,则m、n必须满足的条件是( )
B
课堂练习
3、小试身手 :
1) x2=2 ( )
2) p2 - 49=0 ( )
3) 6 x2=3 ( )
4) (5x+9)2+16=0 ( )
5) 121-(y+3) 2 =0 ( )
×
√
√
√
√
课堂练习
4、解下列方程
(1)x2-1.21=0 (2)4x2-1=0
解:(1)移项,得x2=1.21
∵x是1.21的平方根
∴x=±1.1
即 x1=1.1,x2=-1.1
(2)移项,得4x2=1
两边都除以4,得
∵x是 的平方根
∴x=
即x1= ,x2=
x2=
课堂练习
即x1=-1+
,x2=-1-
5、解下列方程:
⑴(x+1)2= 2
分析:只要将(x+1)看成是一个整体,
就可以运用直接开平方法求解;
解:(1)∵x+1是2的平方根
∴x+1=
∴x+1=
或x+1=
课堂练习
⑵ (x-1)2-4 = 0
∴ x1=3,x2=-1
解:移项,得(x-1)2=4
∵x-1是4的平方根
∴x-1=±2
即x-1=+2 或x-1=-2
⑶ 12(3-2x)2-3 = 0
∴x1= ,
x2=
解:移项,得12(3-2x)2=3
两边都除以12,得(3-2x)2=0.25
∵3-2x是0.25的平方根
∴3-2x=±0.5
即3-2x=0.5或3-2x=-0.5
课堂小结
04
Class summary
课堂小结
首先将一元二次方程化为左边是含有未知数的一个完全平方式,右边是非负数的形式,然后用平方根的概念求解 .
归纳
1.能用直接开平方法解的一元二次方程有什么特点?
如果一个一元二次方程具有x2=a(a≥0)或 (ax+h)2= k(k≥0)的形式,那么就可以用直接开平方法求解.
2.用直接开平方法解一元二次方程的一般步骤是什么?
3.任意一个一元二次方程都能用直接开平方法求解吗?请举例说明.
同课章节目录
