2022-2023学年人教版数学九年级上册21.2.4 根与系数关系 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册21.2.4 根与系数关系 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 09:05:16 | ||
图片预览







文档简介
(共24张PPT)
课程:数学
《根与系数关系》
人教版
九年级上册 第7课时
第 21 章 一元二次方程
教学目标
掌握一元二次方程根与系数的关系,会运用关系定理求已知一元二次方程的两根之和及两根之积,并会解一些简单的问题。
知识与技能
经历一元二次方程根与系数关系的探究过程,培养学生的观察思考、归纳概括能力,在运用关系解决问题的过程中,培养学生解决问题能力,渗透整体的数学思想,求简思想。
过程与方法
通过学生自己探究,发现根与系数的关系,增强学习的信心,培养科学探究精神。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1.一元二次方程的一般形式是什么?
3.一元二次方程的根的情况怎样确定?
2.一元二次方程的求根公式是什么?
新课导入
4、求一个一元二次方程,使它的两个根分别为
①2和3;②-4和7;③3和-8;④-5和-2
x2-5x+6=0
x2-3x-28=0
③(x-3)(x+8)=0
x2+5x-24=0
④(x+5)(x+2)=0
②(x+4)(x-7)=0
①(x-2)(x-3)=0
x2+7x+10=0
问题1:从求这些方程的过程中你发现根
与各项系数之间有什么关系?
探究新知
02
Explore new knowledge
探究新知
如果方程x2+px+q=0有两个根是x1,x2
那么有x1+ x2=-p, x1 x2=q
猜想:2x2-5x+3=0,这个方程的两根之和,两根之积是与各项系数之间有什么关系?
问题2;对于一元二次方程的一般式是否也具备这个特征?
x2=1
解得:x1=
所以得到,x1+x2=
x1 x2=
探究新知
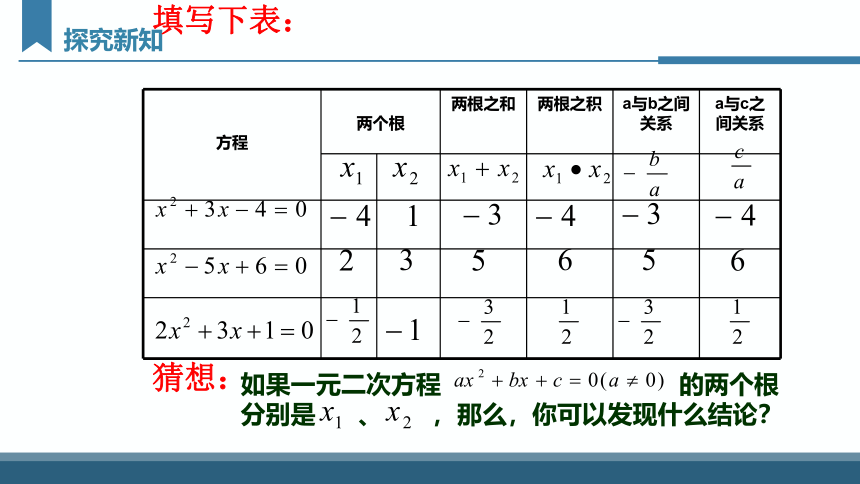
填写下表:
方程 两个根 两根之和 两根之积 a与b之间关系 a与c之间关系
猜想:
如果一元二次方程 的两个根
分别是 、 ,那么,你可以发现什么结论?
探究新知
已知:如果一元二次方程
的两个根分别是 、 。
求证:
探究新知
推导:
探究新知
探究新知
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
探究新知
一元二次方程的
根与系数的关系
16世纪法国最杰出的数学家韦达发现
代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。
课堂练习
03
class exercise
课堂练习
1、如果-1是方程2X2-X+m=0的一个根,则另
一个根是___,m =____。
2、设 X1、X2是方程X2-4X+1=0的两个根,则
X1+X2 = ___ ,X1X2 = ____,
X12+X22 = ( X1+X2)2 - ___ = ___
( X1-X2)2 = ( ___ )2 - 4X1X2 = ___
3、判断正误:
以2和-3为根的方程是X2-X-6=0 ( )
4、已知两个数的和是1,积是-2,则这两个数是
_____ 。
X1+X2
2X1X2
-3
4
1
14
12
×
2和-1
(还有其他解法吗?)
课堂练习
5、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和
解:设方程的两个根是x1 x2,那么
课堂练习
6、已知方程 的一个根是2,求它的另一个根及k的值.
解:设方程 的两个根
分别是 、 ,其中 。
所以:
即:
由于
得:k=-7
答:方程的另一个根是 ,k=-7
课堂练习
7、已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
X1+X2=-k, X1×X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2
解得:k=4 或k=-2
课堂练习
8、方程
有一个正根,一个负根,求m的取值范围。
解:由已知,
△=
{
即
{
m>0
m-1<0
∴0课堂练习
9、方程x2 (m 1)x 2m 1 0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
解: (m 1)2 4(2m 1) m2 6m 5
①∵两根互为相反数
∴两根之和m 1 0,m 1,且 0
∴m 1时,方程的两根互为相反数.
②∵两根互为倒数 m2 6m 5,
∴两根之积2m 1 1 m 1且 0,
∴m 1时,方程的两根互为倒数.
③∵方程一根为0,
∴两根之积2m 1 0 且 0,
∴ 时,方程有一根为零.
课堂小结
04
Class summary
课堂小结
2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式.
3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当 时,才
能应用根与系数的关系.
1.一元二次方程根与系数的关系是什么
总结归纳
课堂练习
以 为两根的一元二次方程
(二次项系数为1)为:
4、已知两根求作新的方程
课程:数学
《根与系数关系》
人教版
九年级上册 第7课时
第 21 章 一元二次方程
教学目标
掌握一元二次方程根与系数的关系,会运用关系定理求已知一元二次方程的两根之和及两根之积,并会解一些简单的问题。
知识与技能
经历一元二次方程根与系数关系的探究过程,培养学生的观察思考、归纳概括能力,在运用关系解决问题的过程中,培养学生解决问题能力,渗透整体的数学思想,求简思想。
过程与方法
通过学生自己探究,发现根与系数的关系,增强学习的信心,培养科学探究精神。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1.一元二次方程的一般形式是什么?
3.一元二次方程的根的情况怎样确定?
2.一元二次方程的求根公式是什么?
新课导入
4、求一个一元二次方程,使它的两个根分别为
①2和3;②-4和7;③3和-8;④-5和-2
x2-5x+6=0
x2-3x-28=0
③(x-3)(x+8)=0
x2+5x-24=0
④(x+5)(x+2)=0
②(x+4)(x-7)=0
①(x-2)(x-3)=0
x2+7x+10=0
问题1:从求这些方程的过程中你发现根
与各项系数之间有什么关系?
探究新知
02
Explore new knowledge
探究新知
如果方程x2+px+q=0有两个根是x1,x2
那么有x1+ x2=-p, x1 x2=q
猜想:2x2-5x+3=0,这个方程的两根之和,两根之积是与各项系数之间有什么关系?
问题2;对于一元二次方程的一般式是否也具备这个特征?
x2=1
解得:x1=
所以得到,x1+x2=
x1 x2=
探究新知
填写下表:
方程 两个根 两根之和 两根之积 a与b之间关系 a与c之间关系
猜想:
如果一元二次方程 的两个根
分别是 、 ,那么,你可以发现什么结论?
探究新知
已知:如果一元二次方程
的两个根分别是 、 。
求证:
探究新知
推导:
探究新知
探究新知
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
探究新知
一元二次方程的
根与系数的关系
16世纪法国最杰出的数学家韦达发现
代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。
课堂练习
03
class exercise
课堂练习
1、如果-1是方程2X2-X+m=0的一个根,则另
一个根是___,m =____。
2、设 X1、X2是方程X2-4X+1=0的两个根,则
X1+X2 = ___ ,X1X2 = ____,
X12+X22 = ( X1+X2)2 - ___ = ___
( X1-X2)2 = ( ___ )2 - 4X1X2 = ___
3、判断正误:
以2和-3为根的方程是X2-X-6=0 ( )
4、已知两个数的和是1,积是-2,则这两个数是
_____ 。
X1+X2
2X1X2
-3
4
1
14
12
×
2和-1
(还有其他解法吗?)
课堂练习
5、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和
解:设方程的两个根是x1 x2,那么
课堂练习
6、已知方程 的一个根是2,求它的另一个根及k的值.
解:设方程 的两个根
分别是 、 ,其中 。
所以:
即:
由于
得:k=-7
答:方程的另一个根是 ,k=-7
课堂练习
7、已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
X1+X2=-k, X1×X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2
解得:k=4 或k=-2
课堂练习
8、方程
有一个正根,一个负根,求m的取值范围。
解:由已知,
△=
{
即
{
m>0
m-1<0
∴0
9、方程x2 (m 1)x 2m 1 0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
解: (m 1)2 4(2m 1) m2 6m 5
①∵两根互为相反数
∴两根之和m 1 0,m 1,且 0
∴m 1时,方程的两根互为相反数.
②∵两根互为倒数 m2 6m 5,
∴两根之积2m 1 1 m 1且 0,
∴m 1时,方程的两根互为倒数.
③∵方程一根为0,
∴两根之积2m 1 0 且 0,
∴ 时,方程有一根为零.
课堂小结
04
Class summary
课堂小结
2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式.
3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当 时,才
能应用根与系数的关系.
1.一元二次方程根与系数的关系是什么
总结归纳
课堂练习
以 为两根的一元二次方程
(二次项系数为1)为:
4、已知两根求作新的方程
同课章节目录
