2022-2023学年人教版数学九年级上册 22.1.2二次函数y=ax2的图象和性质 课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册 22.1.2二次函数y=ax2的图象和性质 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 09:09:25 | ||
图片预览






文档简介
(共23张PPT)
课 程:数 学
《二次函数y=ax2的图象和性质》
人教版
九年级上册 第2课时
第 22 章 二次函数
教学目标
能够利用描点法作出二次函数的图象,并能根据图象认识和理解二次函数y=ax2的性质,初步建立二次函数表达式与图象之间的联系。
知识与技能
经历探索二次函数y=ax2图象和性质的过程,获得利用图象研究函数性质的经验。进一步培养数形结合方法研究函数的性质,了解从特殊到一般的认识过程,学会合情推理。
过程与方法
在数学学习过程中,体验与领悟数学发现的成功感,感受数学发现学习的乐趣。
情感态度和价值观
新课导入
New class introduction
01
探究新知
Explore new knowledge
02
课堂练习
class exercise
03
课堂小结
Class summary
04
目/录
CONTENTS
新课导入
01
New class introduction
新课导入
一般地,形如 y=ax2+bx+c(a、b、c为常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
下列哪些函数是二次函数?哪些是一次函数?
(1) y=3x-l (2) y=2x +7
(4) y=x-2 (5) y=(x+3) -x (6) y=3(x-1) +1
一次函数的图象是一条_____,
(2) 通常怎样画一个函数的图象?
直线
列表、描点、连线
(3) 二次函数的图象是什么形 状呢?
结合图象讨论性质是数形结合的研究函数的重要方法.我们得从最简单的二次函数开始逐步深入地讨论一般二次函数的图象和性质.
探究新知
02
Explore new knowledge
探究新知
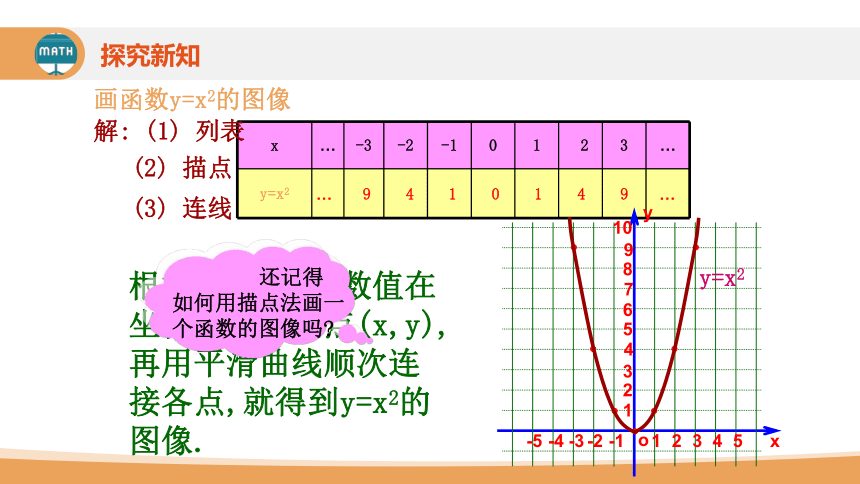
x … -3 -2 -1 0 1 2 3 …
y=x2
画函数y=x2的图像
解: (1) 列表
… 9 4 1 0 1 4 9 …
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
还记得如何用描点法画一个函数的图像吗
y=x2
探究新知
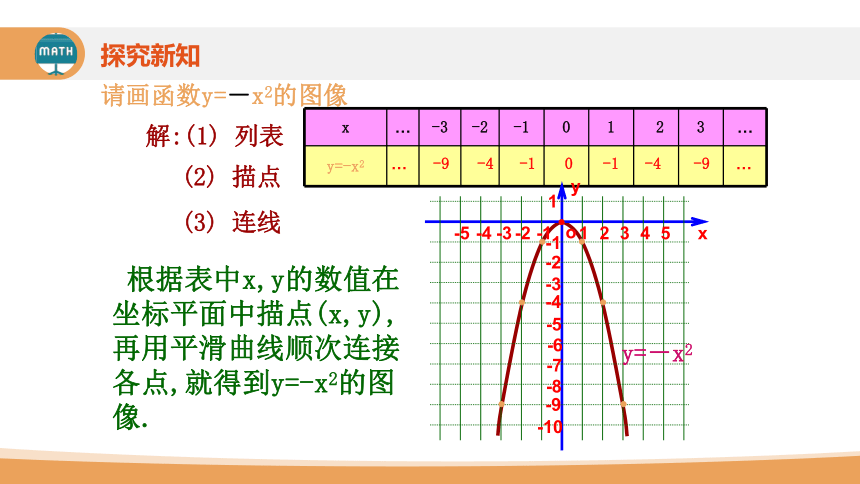
x … -3 -2 -1 0 1 2 3 …
y=-x2
请画函数y=-x2的图像
解:(1) 列表
… -9 -4 -1 0 -1 -4 -9 …
(2) 描点
(3) 连线
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=-x2的图像.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=-x2
探究新知
x
y
o
x
y
o
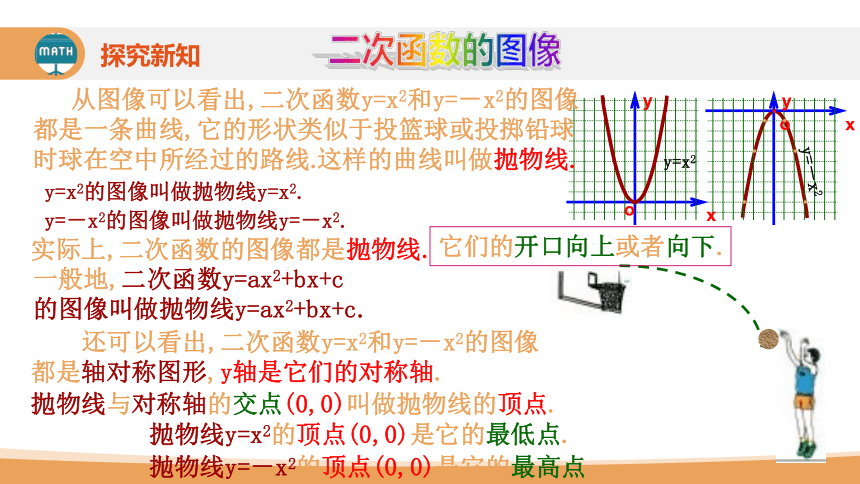
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条曲线,它的形状类似于投篮球或投掷铅球时球在空中所经过的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
y=-x2的图像叫做抛物线y=-x2.
实际上,二次函数的图像都是抛物线.
它们的开口向上或者向下.
一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c.
二次函数的图像
还可以看出,二次函数y=x2和y=-x2的图像都是轴对称图形,y轴是它们的对称轴.
抛物线与对称轴的交点(0,0)叫做抛物线的顶点.
抛物线y=x2的顶点(0,0)是它的最低点.
抛物线y=-x2的顶点(0,0)是它的最高点.
y=x2
y=-x2
探究新知
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴、顶点、最低点、最高点
对称轴与抛物
线的交点叫做
抛物线的顶点.
探究新知
抛物线 y=x2在x轴上方
(除顶点外),顶点是它的最
低点,开口向上,并且向上
无限伸展;
当x=0时,函数 y的值最小,
最小值是0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
探究新知
y
抛物线 y= -x2在x轴下方(除顶点外),顶点
是它的最高点,开口向下,并且向下无限伸展,
当x=0时,函数y的值最大,最大值是0.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
探究新知
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y = x2
y = - x2
(0,0)
(0,0)
y轴
y轴
在x轴上方(除顶点外)
在x轴下方( 除顶点外)
向上
向下
当x=0时,最小值为0
当x=0时,最大值为0
y = x2、y= - x2
探究新知
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小
当a<0时,抛物线的开口向上,顶点是抛物线的最高点,a越小,抛物线的开口越小;
在同一坐标系内,抛物线y=ax2与抛物线y=-ax2是关于x轴对称的.
a>0
a<0
课堂练习
03
class exercise
课堂练习
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在对称轴 侧,y随着x的增大而增大;在对称轴 侧,
y随着x的增大而减小,当x= 时,函数y的值最小,最小
值是 ,抛物线y=2x2在x轴的 方(除顶点外).
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
(0,0)
y轴
右
左
0
0
上
下
增大而增大
增大而减小
0
不等于
课堂练习
2、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解:(1)把(-2,-8)代入y=ax2,得-8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
(2)因为 ,所以点B(-1 ,-4)不在此抛物线上。
(3)由-6=-2x2 ,得x2=3, 所以纵坐标为
-6的点有两个,它们分别是
课堂练习
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
3.在同一直角坐标系中画出函数y= x2和y=2x2的图像
解:(1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点
1
2
课堂练习
4.画出函数y=x2、y=2x2、y= x2的图象:
1
2
y=x2
y=2x2
y= x2
1
2
a>0,开口都向上;
对称轴都是y轴;
增减性相同
只是开口
大小不同
二次项系数越大,
开口越小
顶点都是原点(0,0)
课堂练习
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x … -4 -3 -2 -1 0 1 2 3 4 …
5.在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
解:(1)列表
(2)描点
(3)连线
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=-2x2
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
函数y=- x2,y=-2x2的图像与函数y=-x2(图中虚线图形)的图像相比,有什么共同点和不同点
1
2
1
2
y= - x2
课堂练习
6.函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
7.函数y=-3x2的图象的开口 ,对称轴 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
8.已知 y =(m+1)x 是二次函数且其图象开口向上,求m的值和函数解析式
m2+m
解: 依题意有:
m+1>0 ①
m2+m=2 ②
解②得:m1=-2, m2=1
由①得:m>-1
∴ m=1
此时,二次函数为: y=2x2,
课堂小结
04
Class summary
课堂小结
1. 二次函数的图像都是抛物线.
2. 抛物线y=ax2的图像性质:
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
|a|越大,抛物线的开口越小;
(1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
x
y
o
a>0
a<0
a<0
x
y
o
课 程:数 学
《二次函数y=ax2的图象和性质》
人教版
九年级上册 第2课时
第 22 章 二次函数
教学目标
能够利用描点法作出二次函数的图象,并能根据图象认识和理解二次函数y=ax2的性质,初步建立二次函数表达式与图象之间的联系。
知识与技能
经历探索二次函数y=ax2图象和性质的过程,获得利用图象研究函数性质的经验。进一步培养数形结合方法研究函数的性质,了解从特殊到一般的认识过程,学会合情推理。
过程与方法
在数学学习过程中,体验与领悟数学发现的成功感,感受数学发现学习的乐趣。
情感态度和价值观
新课导入
New class introduction
01
探究新知
Explore new knowledge
02
课堂练习
class exercise
03
课堂小结
Class summary
04
目/录
CONTENTS
新课导入
01
New class introduction
新课导入
一般地,形如 y=ax2+bx+c(a、b、c为常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
下列哪些函数是二次函数?哪些是一次函数?
(1) y=3x-l (2) y=2x +7
(4) y=x-2 (5) y=(x+3) -x (6) y=3(x-1) +1
一次函数的图象是一条_____,
(2) 通常怎样画一个函数的图象?
直线
列表、描点、连线
(3) 二次函数的图象是什么形 状呢?
结合图象讨论性质是数形结合的研究函数的重要方法.我们得从最简单的二次函数开始逐步深入地讨论一般二次函数的图象和性质.
探究新知
02
Explore new knowledge
探究新知
x … -3 -2 -1 0 1 2 3 …
y=x2
画函数y=x2的图像
解: (1) 列表
… 9 4 1 0 1 4 9 …
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
还记得如何用描点法画一个函数的图像吗
y=x2
探究新知
x … -3 -2 -1 0 1 2 3 …
y=-x2
请画函数y=-x2的图像
解:(1) 列表
… -9 -4 -1 0 -1 -4 -9 …
(2) 描点
(3) 连线
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=-x2的图像.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=-x2
探究新知
x
y
o
x
y
o
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条曲线,它的形状类似于投篮球或投掷铅球时球在空中所经过的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
y=-x2的图像叫做抛物线y=-x2.
实际上,二次函数的图像都是抛物线.
它们的开口向上或者向下.
一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c.
二次函数的图像
还可以看出,二次函数y=x2和y=-x2的图像都是轴对称图形,y轴是它们的对称轴.
抛物线与对称轴的交点(0,0)叫做抛物线的顶点.
抛物线y=x2的顶点(0,0)是它的最低点.
抛物线y=-x2的顶点(0,0)是它的最高点.
y=x2
y=-x2
探究新知
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴、顶点、最低点、最高点
对称轴与抛物
线的交点叫做
抛物线的顶点.
探究新知
抛物线 y=x2在x轴上方
(除顶点外),顶点是它的最
低点,开口向上,并且向上
无限伸展;
当x=0时,函数 y的值最小,
最小值是0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
探究新知
y
抛物线 y= -x2在x轴下方(除顶点外),顶点
是它的最高点,开口向下,并且向下无限伸展,
当x=0时,函数y的值最大,最大值是0.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
探究新知
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y = x2
y = - x2
(0,0)
(0,0)
y轴
y轴
在x轴上方(除顶点外)
在x轴下方( 除顶点外)
向上
向下
当x=0时,最小值为0
当x=0时,最大值为0
y = x2、y= - x2
探究新知
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小
当a<0时,抛物线的开口向上,顶点是抛物线的最高点,a越小,抛物线的开口越小;
在同一坐标系内,抛物线y=ax2与抛物线y=-ax2是关于x轴对称的.
a>0
a<0
课堂练习
03
class exercise
课堂练习
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,
在对称轴 侧,y随着x的增大而增大;在对称轴 侧,
y随着x的增大而减小,当x= 时,函数y的值最小,最小
值是 ,抛物线y=2x2在x轴的 方(除顶点外).
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
(0,0)
y轴
右
左
0
0
上
下
增大而增大
增大而减小
0
不等于
课堂练习
2、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解:(1)把(-2,-8)代入y=ax2,得-8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
(2)因为 ,所以点B(-1 ,-4)不在此抛物线上。
(3)由-6=-2x2 ,得x2=3, 所以纵坐标为
-6的点有两个,它们分别是
课堂练习
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
3.在同一直角坐标系中画出函数y= x2和y=2x2的图像
解:(1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点
1
2
课堂练习
4.画出函数y=x2、y=2x2、y= x2的图象:
1
2
y=x2
y=2x2
y= x2
1
2
a>0,开口都向上;
对称轴都是y轴;
增减性相同
只是开口
大小不同
二次项系数越大,
开口越小
顶点都是原点(0,0)
课堂练习
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x … -4 -3 -2 -1 0 1 2 3 4 …
5.在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
解:(1)列表
(2)描点
(3)连线
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=-2x2
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
函数y=- x2,y=-2x2的图像与函数y=-x2(图中虚线图形)的图像相比,有什么共同点和不同点
1
2
1
2
y= - x2
课堂练习
6.函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
7.函数y=-3x2的图象的开口 ,对称轴 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
8.已知 y =(m+1)x 是二次函数且其图象开口向上,求m的值和函数解析式
m2+m
解: 依题意有:
m+1>0 ①
m2+m=2 ②
解②得:m1=-2, m2=1
由①得:m>-1
∴ m=1
此时,二次函数为: y=2x2,
课堂小结
04
Class summary
课堂小结
1. 二次函数的图像都是抛物线.
2. 抛物线y=ax2的图像性质:
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
|a|越大,抛物线的开口越小;
(1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
x
y
o
a>0
a<0
a<0
x
y
o
同课章节目录
