2022—2023学年人教版数学九年级上册 第22章 二次函第9课时《实际问题与二次函数》课件(共25张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册 第22章 二次函第9课时《实际问题与二次函数》课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 11:13:07 | ||
图片预览







文档简介
(共25张PPT)
课程:数学
《实际问题与二次函数》
人教版
九年级上册 第9课时
第 22 章 二次函数
教学目标
1
2
3
知识与技能
掌握二次函数的解析式求法,能灵活运用抛物线的解析式的求法和图象的性质知识解一些实际问题。
过程与方法
通过观察、猜想、验证、推理、交流等数学活动进一步发展学生的演绎推理能力和发散思维能力。
情感态度和价值观
经历探索二次函数相关题目的过程,体会数形结合思想、化归思想在数学中的广泛应用,同时感受数学知识来源于实际生活,反之,又服务于实际生活.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
-2
0
2
4
6
2
-4
x
y
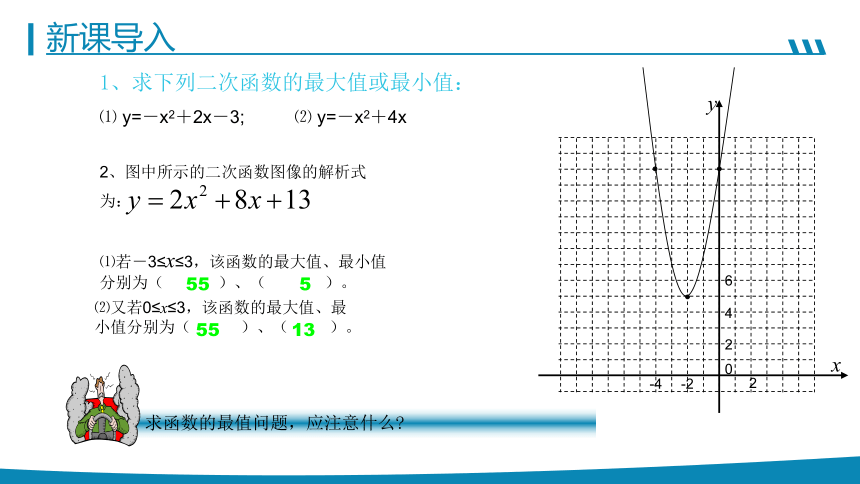
⑴若-3≤x≤3,该函数的最大值、最小值分别为( )、( )。
⑵又若0≤x≤3,该函数的最大值、最小值分别为( )、( )。
求函数的最值问题,应注意什么
55 5
55 13
2、图中所示的二次函数图像的解析式
为:
1、求下列二次函数的最大值或最小值:
⑴ y=-x2+2x-3; ⑵ y=-x2+4x
新课导入
02
PART TWO
探究新知
Explore new knowledge
探究新知
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
请大家带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
探究新知
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,销额为 元,买进商品需付 元因此,所得利润为 元
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
y=(60+x)(300-10x)-40(300-10x)
即
(0≤X≤30)
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标.
探究新知
(0≤X≤30)
所以,当定价为65元时,利润最大,最大利润为6250元
探究新知
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。
解:设降价x元时利润最大,则每星期可多卖18x件,实际卖出(300+18x)件,销售额为(60-x)(300+18x)元,买进商品需付40(300-10x)元,因此,得利润
答:定价为 元时,利润最大,最大利润为6050元
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
(0≤x≤20)
探究新知
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
解这类题目的一般步骤
探究新知
一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。
问此球能否投中?
3米
8米
4米
4米
探究新知
8
(4,4)
如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:
(0≤x≤8)
(0≤x≤8)
∵篮圈中心距离地面3米
∴此球不能投中
探究新知
若假设出手的角度和力度都不变,
则如何才能使此球命中
探究
(1)跳得高一点
(2)向前平移一点
探究新知
y
x
(4,4)
(8,3)
在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈
0 1 2 3 4 5 6 7 8 9
探究新知
y
X
(8,3)
(5,4)
(4,4)
0 1 2 3 4 5 6 7 8 9
在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?
(7,3)●
PART THREE
课堂练习
class exercise
03
课堂练习
1、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 。
9或1
2、写出一个开口向下,对称轴是直线x=3,且与y轴交于(0,-2)的抛物线解析式。
探究新知
3、把抛物线y=-3x2绕着它的顶点旋转1800后所得的图象解析式是 。
y=3x2
4、已知二次函数y=a(x-h)2+k的图象过原点,最小值是-8,且形状与抛物线y=0.5x2-3x-5的形状相同,其解析式为 。
y=0.5(x-16)2-8
5、若x为任意实数,则二次函数y=x2+2x+3的函数值y的取值范围是 。
y≥2
探究新知
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。
7、已知抛物线y=2x2+bx+8的顶点在x轴上,则b= 。
8
3
±8
8、已知y=x2-(12-k)x+12,当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,则k的值为 。
10
探究新知
问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?
x
y
o
1. 如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m.
3.05 m
2.5m
3.5m
问题1 建立如图所示的直角坐标系,求抛物线的解析式;
4 m
综合应用 (中考必考题)
探究新知
2.你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
用抛物线的知识解决运动场上或者生活中的一些实际问题的一般步骤:
建立直角坐标系
二次函数
问题求解
找出实际问题的答案
及
时
总
结
课程:数学
《实际问题与二次函数》
人教版
九年级上册 第9课时
第 22 章 二次函数
教学目标
1
2
3
知识与技能
掌握二次函数的解析式求法,能灵活运用抛物线的解析式的求法和图象的性质知识解一些实际问题。
过程与方法
通过观察、猜想、验证、推理、交流等数学活动进一步发展学生的演绎推理能力和发散思维能力。
情感态度和价值观
经历探索二次函数相关题目的过程,体会数形结合思想、化归思想在数学中的广泛应用,同时感受数学知识来源于实际生活,反之,又服务于实际生活.
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
-2
0
2
4
6
2
-4
x
y
⑴若-3≤x≤3,该函数的最大值、最小值分别为( )、( )。
⑵又若0≤x≤3,该函数的最大值、最小值分别为( )、( )。
求函数的最值问题,应注意什么
55 5
55 13
2、图中所示的二次函数图像的解析式
为:
1、求下列二次函数的最大值或最小值:
⑴ y=-x2+2x-3; ⑵ y=-x2+4x
新课导入
02
PART TWO
探究新知
Explore new knowledge
探究新知
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
请大家带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
探究新知
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
来到商场
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品的利润y也随之变化,我们先来确定y与x的函数关系式。涨价x元时则每星期少卖 件,实际卖出 件,销额为 元,买进商品需付 元因此,所得利润为 元
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
y=(60+x)(300-10x)-40(300-10x)
即
(0≤X≤30)
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标.
探究新知
(0≤X≤30)
所以,当定价为65元时,利润最大,最大利润为6250元
探究新知
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案。
解:设降价x元时利润最大,则每星期可多卖18x件,实际卖出(300+18x)件,销售额为(60-x)(300+18x)元,买进商品需付40(300-10x)元,因此,得利润
答:定价为 元时,利润最大,最大利润为6050元
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
(0≤x≤20)
探究新知
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
解这类题目的一般步骤
探究新知
一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。
问此球能否投中?
3米
8米
4米
4米
探究新知
8
(4,4)
如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:
(0≤x≤8)
(0≤x≤8)
∵篮圈中心距离地面3米
∴此球不能投中
探究新知
若假设出手的角度和力度都不变,
则如何才能使此球命中
探究
(1)跳得高一点
(2)向前平移一点
探究新知
y
x
(4,4)
(8,3)
在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈
0 1 2 3 4 5 6 7 8 9
探究新知
y
X
(8,3)
(5,4)
(4,4)
0 1 2 3 4 5 6 7 8 9
在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?
(7,3)●
PART THREE
课堂练习
class exercise
03
课堂练习
1、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 。
9或1
2、写出一个开口向下,对称轴是直线x=3,且与y轴交于(0,-2)的抛物线解析式。
探究新知
3、把抛物线y=-3x2绕着它的顶点旋转1800后所得的图象解析式是 。
y=3x2
4、已知二次函数y=a(x-h)2+k的图象过原点,最小值是-8,且形状与抛物线y=0.5x2-3x-5的形状相同,其解析式为 。
y=0.5(x-16)2-8
5、若x为任意实数,则二次函数y=x2+2x+3的函数值y的取值范围是 。
y≥2
探究新知
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。
7、已知抛物线y=2x2+bx+8的顶点在x轴上,则b= 。
8
3
±8
8、已知y=x2-(12-k)x+12,当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,则k的值为 。
10
探究新知
问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?
x
y
o
1. 如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m.
3.05 m
2.5m
3.5m
问题1 建立如图所示的直角坐标系,求抛物线的解析式;
4 m
综合应用 (中考必考题)
探究新知
2.你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
用抛物线的知识解决运动场上或者生活中的一些实际问题的一般步骤:
建立直角坐标系
二次函数
问题求解
找出实际问题的答案
及
时
总
结
同课章节目录
