2022—2023学年人教版数学九年级上册 第22章 二次函数第1课时《二次函数的意义》课件(共26张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册 第22章 二次函数第1课时《二次函数的意义》课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 11:13:36 | ||
图片预览








文档简介
(共26张PPT)
课程:数学
《二次函数的意义》
人教版
九年级上册 第1课时
第 22 章 二次函数
教学目标
1
2
3
知识与技能
1.探索并归纳二次函数的定义;2.能够表示简单变量之间的二次函数关系。
过程与方法
1.感悟新旧知识间的关系,让学生更深刻地体会数学中的类比思想方法;
2.经历探索、分析和建立两个变量之间的二次函数关系的过程,进一步体验如何用数学的方法描述变量之间的数量关系。
情感态度和价值观
把数学问题和实际问题相联系,从学生感兴趣的问题入手,能使学生积极参与数学学习活动,对数学有好奇心和求知欲。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
温故知新 什么叫函数
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫因变量。
目前,我们已经学习了那几种类型的函数?
探究新知
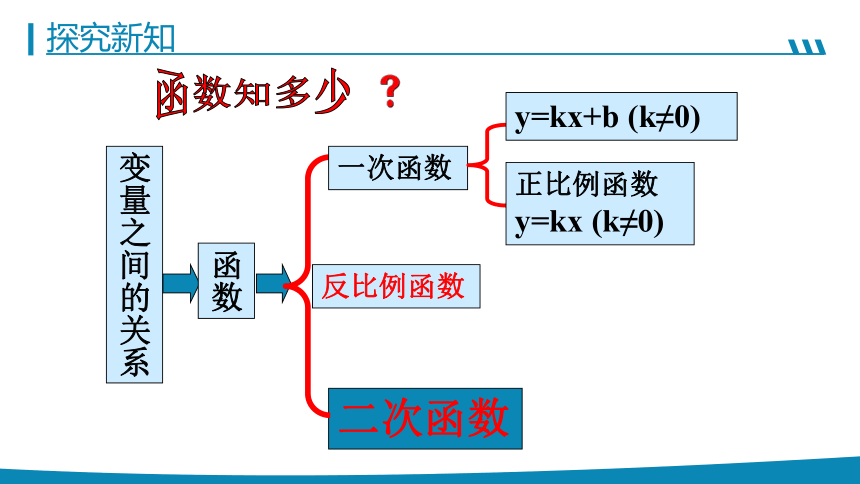
二次函数
函数知多少
变量之间的关系
函数
一次函数
反比例函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
02
PART TWO
探究新知
Explore new knowledge
探究新知
二次函数
探究新知
y=6x2
问题1:正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为 .
此式表示了正方体表面积y与正方体棱长x之间的关系,对于y的每一个值,x都有唯一的一个对应值,即y是x的函数。
探究新知
问题2:n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
每个球队n要与其他(n-1)个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛时同一场比赛,所以比赛的场次数
即
此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有唯一的一个对应值,即m是n的函数。
探究新知
问题3:多边形的对角线数d与边数n有什么关系?
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
N
M
n
(n-3)
即
此式表示了多边形的对角线数d与边数n之间的关系,对于n的每一值,d都有唯一的对应值,即d是n的函数。
探究新知
问题4:某工厂一种产品现在的年产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
20(1+x)
20(1+x)2
即
这种产品的原产量是20件, 一年后的产量是
件,再经过一年后的产量是 件,即两年后的产量y=__________
20(1+x)2
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数。
探究新知
函数都是用自变量的二次整式表示的
一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中a为二次项系数,b为一次项系数,c为常数项。
式子①②③④有什么共同点
y=6x2
探究新知
2、定义:一般地,形y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)等号左边是变量y,右边是关于自变量x的
(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。
注意:
(2)a,b,c为常数,且
(4)x的取值范围是 。
整式
a≠0.
2
任意实数
探究新知
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1)y=3(x-1) +1 (2)y=x+3
(3)s=3-2t (4)y=(x+3) -x
(5)y= (6)v=10 r
x
1
__
探究新知
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
当a、b、c为何值时函数y=ax2+bx+c是一次函数?
正比例函数?
探究新知
思考: 二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
你知道吗
联系(1)等式一边都是ax2+bx+c且 a ≠0 (2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
PART THREE
课堂练习
class exercise
03
课堂练习
1.下列函数中,哪些是二次函数?
(1) y=3(x-1) +1
(3) s=3-2t
(5)y=(x+3) -x
(6)v=10πr
(是)
(否)
(是)
(否)
(否)
(是)
(7) y=x +x +25
(8)y=2 +2x
(否)
(否)
(2)
探究新知
2、下列函数中,哪些是二次函数?
否
是
否
否
是
探究新知
3、关于x的函数 是二次函数, 求m的值.
解: 由题意可得
注意:二次函数的二次项系数不能为零
探究新知
4、若函数 为二次函数,求m的值。
解:因为该函数为二次函数,
则
解(1)得:m=2或-1
解(2)得:
所以m=2
探究新知
5、已知函数
(1) k为何值时,y是x的一次函数?
(2) k为何值时,y是x的二次函数?
解(1)根据题意得
∴k=1时,y是x的一次函数。
探究新知
6、已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.
{
待定系数法
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
二次函数的x的范围为:
注意:
1. 自变量的最高次数是2。
2. 二次项的系数a≠0,可以没有一次项和常数项,但不能没有二次项。
3. 二次函数解析式必须是整式。
一切实数。
其中,x是自变量,ax2是二次项,a是二次向系数
bx是一次项,b是一次项系数
c是常数项。
一般地,形如 y=ax2+bx+c(a,b,c是常数,a 0)
的函数,叫做二次函数。
二次函数的定义:
课程:数学
《二次函数的意义》
人教版
九年级上册 第1课时
第 22 章 二次函数
教学目标
1
2
3
知识与技能
1.探索并归纳二次函数的定义;2.能够表示简单变量之间的二次函数关系。
过程与方法
1.感悟新旧知识间的关系,让学生更深刻地体会数学中的类比思想方法;
2.经历探索、分析和建立两个变量之间的二次函数关系的过程,进一步体验如何用数学的方法描述变量之间的数量关系。
情感态度和价值观
把数学问题和实际问题相联系,从学生感兴趣的问题入手,能使学生积极参与数学学习活动,对数学有好奇心和求知欲。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
温故知新 什么叫函数
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫因变量。
目前,我们已经学习了那几种类型的函数?
探究新知
二次函数
函数知多少
变量之间的关系
函数
一次函数
反比例函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
02
PART TWO
探究新知
Explore new knowledge
探究新知
二次函数
探究新知
y=6x2
问题1:正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为 .
此式表示了正方体表面积y与正方体棱长x之间的关系,对于y的每一个值,x都有唯一的一个对应值,即y是x的函数。
探究新知
问题2:n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
每个球队n要与其他(n-1)个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛时同一场比赛,所以比赛的场次数
即
此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有唯一的一个对应值,即m是n的函数。
探究新知
问题3:多边形的对角线数d与边数n有什么关系?
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
N
M
n
(n-3)
即
此式表示了多边形的对角线数d与边数n之间的关系,对于n的每一值,d都有唯一的对应值,即d是n的函数。
探究新知
问题4:某工厂一种产品现在的年产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
20(1+x)
20(1+x)2
即
这种产品的原产量是20件, 一年后的产量是
件,再经过一年后的产量是 件,即两年后的产量y=__________
20(1+x)2
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数。
探究新知
函数都是用自变量的二次整式表示的
一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中a为二次项系数,b为一次项系数,c为常数项。
式子①②③④有什么共同点
y=6x2
探究新知
2、定义:一般地,形y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)等号左边是变量y,右边是关于自变量x的
(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。
注意:
(2)a,b,c为常数,且
(4)x的取值范围是 。
整式
a≠0.
2
任意实数
探究新知
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项.
(1)y=3(x-1) +1 (2)y=x+3
(3)s=3-2t (4)y=(x+3) -x
(5)y= (6)v=10 r
x
1
__
探究新知
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
当a、b、c为何值时函数y=ax2+bx+c是一次函数?
正比例函数?
探究新知
思考: 二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
你知道吗
联系(1)等式一边都是ax2+bx+c且 a ≠0 (2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
PART THREE
课堂练习
class exercise
03
课堂练习
1.下列函数中,哪些是二次函数?
(1) y=3(x-1) +1
(3) s=3-2t
(5)y=(x+3) -x
(6)v=10πr
(是)
(否)
(是)
(否)
(否)
(是)
(7) y=x +x +25
(8)y=2 +2x
(否)
(否)
(2)
探究新知
2、下列函数中,哪些是二次函数?
否
是
否
否
是
探究新知
3、关于x的函数 是二次函数, 求m的值.
解: 由题意可得
注意:二次函数的二次项系数不能为零
探究新知
4、若函数 为二次函数,求m的值。
解:因为该函数为二次函数,
则
解(1)得:m=2或-1
解(2)得:
所以m=2
探究新知
5、已知函数
(1) k为何值时,y是x的一次函数?
(2) k为何值时,y是x的二次函数?
解(1)根据题意得
∴k=1时,y是x的一次函数。
探究新知
6、已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.
{
待定系数法
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
二次函数的x的范围为:
注意:
1. 自变量的最高次数是2。
2. 二次项的系数a≠0,可以没有一次项和常数项,但不能没有二次项。
3. 二次函数解析式必须是整式。
一切实数。
其中,x是自变量,ax2是二次项,a是二次向系数
bx是一次项,b是一次项系数
c是常数项。
一般地,形如 y=ax2+bx+c(a,b,c是常数,a 0)
的函数,叫做二次函数。
二次函数的定义:
同课章节目录
