人教版数学七年级上册 1.5.3 近似数 教案
文档属性
| 名称 | 人教版数学七年级上册 1.5.3 近似数 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 294.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 11:22:23 | ||
图片预览



文档简介
第一章 有理数
1.5 有理数的乘方
1.5.3 近似数
一、教学目标
【知识与技能】
1.给了一个近似数,你能说出它精确到哪一位.
2.给了一个数,会按照精确到要求哪一位,四舍五入取近似数.
3.会识别一个数是近似数或准确数.
【过程与方法】
从测量引入近似数,使学生体会近似数的意义和生活中的应用.
【情感态度与价值观】
培养学生认真细致的学习态度,合作交流的意识.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
近似数、精确度的意义.
【教学难点】
由给出的近似数求其精确度及有效数字,按给定的精确或有效数一个数的近似数.
五、课前准备
教师:课件、直尺、数据图片等。
学生:三角尺、练习本、铅笔、圆珠笔或钢笔。
六、教学过程
(一)导入新课
北京地铁1号线是我国最早的地铁路线,全长31.04公里.“31.04”一定是准确的数据吗?它又是怎么来的?(出示课件2)
(二)探索新知
1.师生互动,探究近似数
教师问1:下列语句中,哪些数据是精确的,哪些数据是近似的?(出示课件4)
1.妈妈去买水果,买了 8 个苹果,大约 3 千克.
2.小民与小李买了 2 瓶水,4 根黄瓜,6 袋香巴拉牛肉干,约 20 元,然后骑车去大约 3.5 km外去郊游,大约玩了 4.5 小时回家.
3.我国共有 56 个民族.
学生回答:精确数:8,2,4,6,56;近似数:3,20,3.5,4.5.
教师问2:什么样的数是近似数?你能举例说明吗?(出示课件5)
学生回答:1.我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数. 例如,姚明的身高是2.26米.2.有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数. 例如,2021年全国高考报名的考生共178万人.
教师问3:判断下列各数,哪些是近似数,哪些是准确数.(出示课件6)
(1)某歌星在体育馆举办音乐会,大约有一万二千人参加. (2)检查一双没洗过的手,发现带有各种细菌800000万个. (3) 张明家里养了5只鸡.
(4) 据统计,2017年全国初中在校生人数为4311.95万.
学生回答:(1)近似数;(2)近似数;(3)准确数;(4)近似数.
2.师生互动,探究按要求求近似值
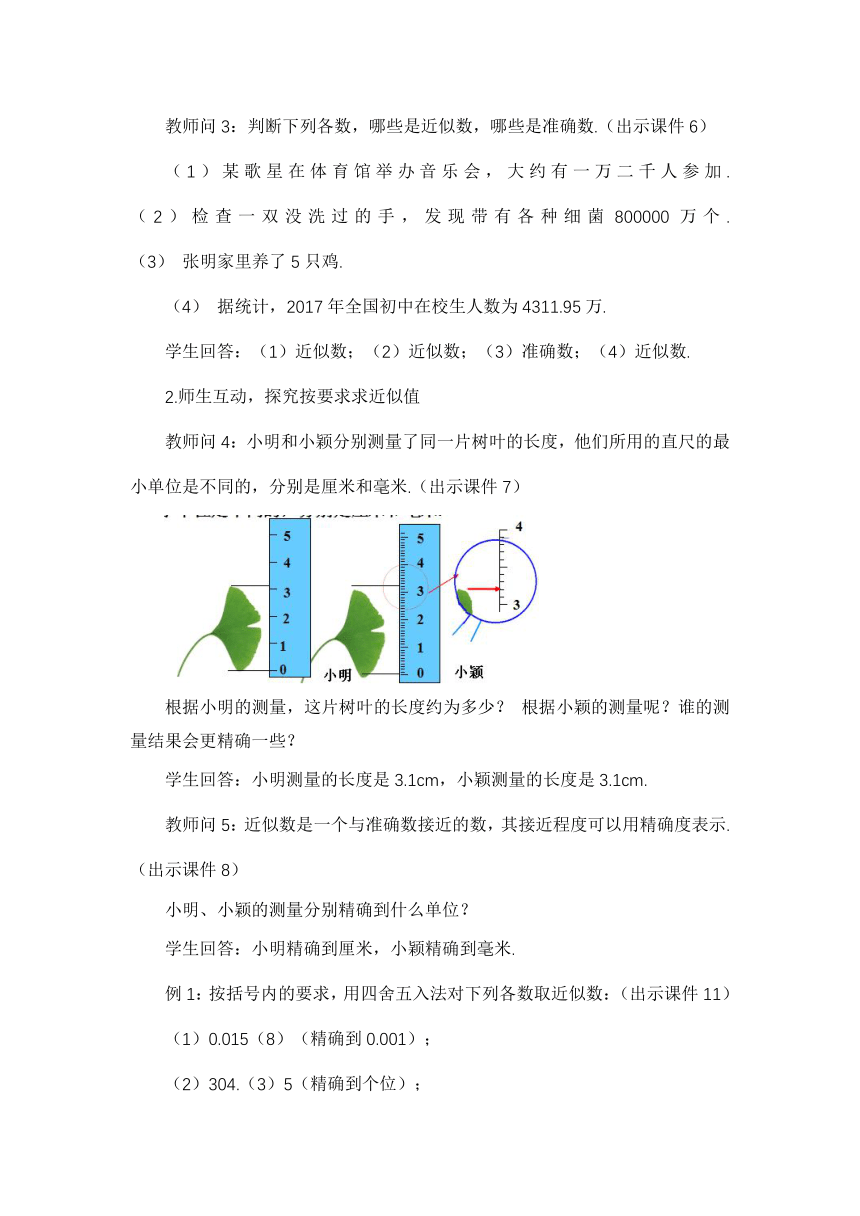
教师问4:小明和小颖分别测量了同一片树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.(出示课件7)
根据小明的测量,这片树叶的长度约为多少? 根据小颖的测量呢?谁的测量结果会更精确一些?
学生回答:小明测量的长度是3.1cm,小颖测量的长度是3.1cm.
教师问5:近似数是一个与准确数接近的数,其接近程度可以用精确度表示.(出示课件8)
小明、小颖的测量分别精确到什么单位?
学生回答:小明精确到厘米,小颖精确到毫米.
例1:按括号内的要求,用四舍五入法对下列各数取近似数:(出示课件11)
(1)0.015(8)(精确到0.001);
(2)304.(3)5(精确到个位);
(3)1.8(0)4(精确到0.1);
(4)1.80(4)(精确到0.01).
师生共同解答如下:
解:(1)对8四舍五入,0.0158 ≈0.016
(2)对3四舍五入,304.35≈304
(3)对0四舍五入,1.804 ≈1.8
(4)对4四舍五入,1.804≈1.80.
教师问6:(4)中能把“1.80”后面的“0”去掉吗?
学生回答:(4)题中,1.80,这里的0不能去掉,由四舍五入得到的1.8与1.80的精确度是不同的,前者是精确到0.1,而后者是精确到0.01.
例2:下列由四舍五入得到的近似数,各精确到哪一位?(出示课件13)
(1) 600万 ; (2) 7.03万;
(3) 5.8亿 ; (4) 3.30×105.
师生共同解答如下:
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
总结点拨:看一个近似数精确到哪一位,就要看它四舍五入到哪一位. 对带上了单位的近似数,应先将它还原成不带单位的数.
例3:据2010年上海世博会官方统计,2010年5月1日至10月31日期间,共有7308.44万人次入园参观,求每天平均入园人次(精确到0.01万人次).(出示课件15)
师生共同解答如下:
解:从5月1日至10月31日共有184天,故每天的平均入园人次为
7308.44÷184≈39.719≈39.72(万人次).
(三)课堂练习(出示课件17-31)
1.5月18 日,新华社电讯:我国利用世界唯一的“蓝鲸1号”,在南海实现了可燃冰(即天然气水合物)的安全可控开采.据介绍,“蓝鲸1号”拥有27354台设备,约40000根管路,约50 000个MCC报验点,电缆拉放长度估计1200千米.其中准确数是( )
A.27354 B.40000 C.50000 D.1200
2. 近似数5.0×102精确到( )
A.十分位 B.个位 C.十位 D.百位
3.用四舍五入法按要求取近似值:
(1)75 436(精确到百位)
(2)0.785(精确到百分位)
4.下列数据精确到什么位?
(1)小王的身高1.53米;
(2)月球与地球相距38万千米;
(3)圆周率π取3.14159.
5.判断下列说法是否正确,说明理由.
(1)近似数4.60与4.6的精确度相同.
(2)近似数5千万与近似数5000万的精确度相同.
(3)近似4.31万精确到0.01.
(4)1.45×104 精确到0.01.
6.某校七年级共有学生112名,想租用45座的客车外出参观,应租几辆客车?
7.若2m布可做1件衣服,则9m能做多少件这样的衣服?
参考答案:
1.A
2.C
3.解:(1)75 436≈7.54×104 ;(2)0.785≈0.79
4.解:(1)精确到0.01;(2)精确到万位;(3)精确到0.00001
5.解:(1)错,近似数4.60精确到0.01,近似数4.6精确到0.1.
(2)错,近似数5千万精确到千万位,近似数5000万精确到万位.
(3)错,近似数4.31万写成单位为‘个’位的数是43100,数字1所在的位置为百位,故4.31万精确到百位.
(4)错,1.45×104 写成原数为14500,数字5所在位置为百位,故1.45×104精确到百位.
6.解:112÷45=2.488… ≈3(辆).
7.解:9÷2=4.5≈4(件).
(四)课堂小结
今天我们学了哪些内容:
正确理解和掌握近似数、准确实的概念,给出一个近似数,能准确地确定它精确到哪一位,并能按要求求一个数的近似数.
(五)课前预习
预习下节课(2.1)54页到55页的相关内容。
知道用字母表示数和含有字母的式子表示实际问题中的数量关系
七、课后作业
1、教材46页练习
2、下列是由四舍五入法得到的近似数,各精确到哪一位?保留几个有效数字?
(1)132.4; (2)0.0572; (3)2.40万; (4)3000.
八、板书设计:
1.判断准确数与近似数
2.按照要求取近似数.
四舍五入到某一位,就说这个数的近似数精确到那一位.
3.由近似数判断精确度.
九、教学反思:
1.本节课以学生课前收集的生活数据引,使学生获得了直观的体验,认识到数学来源于生活,认识到生活中存在着准确数和近似数,在了解近似数以后,启发学生“生活中还有什么地方用到近似数?”并通过教师自己设计的情境使学生认识到有时是因为客观条件无法或难以得到准确数据,有时是实际问题无需得到准确数据。
2.补充例题以生活实际为背景,不过数据有些大,学生容易出错,教师要提醒学生注意。
3.鼓励学生去查资料,收集资料,培养数感。当数据较大或较小时,适宜 用科学记数法表示,鼓励学生观察生活中的数据,养成良好的数学学习习惯,同时使学生能深深地体会到我们生活在数的世界中。
1.5 有理数的乘方
1.5.3 近似数
一、教学目标
【知识与技能】
1.给了一个近似数,你能说出它精确到哪一位.
2.给了一个数,会按照精确到要求哪一位,四舍五入取近似数.
3.会识别一个数是近似数或准确数.
【过程与方法】
从测量引入近似数,使学生体会近似数的意义和生活中的应用.
【情感态度与价值观】
培养学生认真细致的学习态度,合作交流的意识.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
近似数、精确度的意义.
【教学难点】
由给出的近似数求其精确度及有效数字,按给定的精确或有效数一个数的近似数.
五、课前准备
教师:课件、直尺、数据图片等。
学生:三角尺、练习本、铅笔、圆珠笔或钢笔。
六、教学过程
(一)导入新课
北京地铁1号线是我国最早的地铁路线,全长31.04公里.“31.04”一定是准确的数据吗?它又是怎么来的?(出示课件2)
(二)探索新知
1.师生互动,探究近似数
教师问1:下列语句中,哪些数据是精确的,哪些数据是近似的?(出示课件4)
1.妈妈去买水果,买了 8 个苹果,大约 3 千克.
2.小民与小李买了 2 瓶水,4 根黄瓜,6 袋香巴拉牛肉干,约 20 元,然后骑车去大约 3.5 km外去郊游,大约玩了 4.5 小时回家.
3.我国共有 56 个民族.
学生回答:精确数:8,2,4,6,56;近似数:3,20,3.5,4.5.
教师问2:什么样的数是近似数?你能举例说明吗?(出示课件5)
学生回答:1.我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数. 例如,姚明的身高是2.26米.2.有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数. 例如,2021年全国高考报名的考生共178万人.
教师问3:判断下列各数,哪些是近似数,哪些是准确数.(出示课件6)
(1)某歌星在体育馆举办音乐会,大约有一万二千人参加. (2)检查一双没洗过的手,发现带有各种细菌800000万个. (3) 张明家里养了5只鸡.
(4) 据统计,2017年全国初中在校生人数为4311.95万.
学生回答:(1)近似数;(2)近似数;(3)准确数;(4)近似数.
2.师生互动,探究按要求求近似值
教师问4:小明和小颖分别测量了同一片树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.(出示课件7)
根据小明的测量,这片树叶的长度约为多少? 根据小颖的测量呢?谁的测量结果会更精确一些?
学生回答:小明测量的长度是3.1cm,小颖测量的长度是3.1cm.
教师问5:近似数是一个与准确数接近的数,其接近程度可以用精确度表示.(出示课件8)
小明、小颖的测量分别精确到什么单位?
学生回答:小明精确到厘米,小颖精确到毫米.
例1:按括号内的要求,用四舍五入法对下列各数取近似数:(出示课件11)
(1)0.015(8)(精确到0.001);
(2)304.(3)5(精确到个位);
(3)1.8(0)4(精确到0.1);
(4)1.80(4)(精确到0.01).
师生共同解答如下:
解:(1)对8四舍五入,0.0158 ≈0.016
(2)对3四舍五入,304.35≈304
(3)对0四舍五入,1.804 ≈1.8
(4)对4四舍五入,1.804≈1.80.
教师问6:(4)中能把“1.80”后面的“0”去掉吗?
学生回答:(4)题中,1.80,这里的0不能去掉,由四舍五入得到的1.8与1.80的精确度是不同的,前者是精确到0.1,而后者是精确到0.01.
例2:下列由四舍五入得到的近似数,各精确到哪一位?(出示课件13)
(1) 600万 ; (2) 7.03万;
(3) 5.8亿 ; (4) 3.30×105.
师生共同解答如下:
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
总结点拨:看一个近似数精确到哪一位,就要看它四舍五入到哪一位. 对带上了单位的近似数,应先将它还原成不带单位的数.
例3:据2010年上海世博会官方统计,2010年5月1日至10月31日期间,共有7308.44万人次入园参观,求每天平均入园人次(精确到0.01万人次).(出示课件15)
师生共同解答如下:
解:从5月1日至10月31日共有184天,故每天的平均入园人次为
7308.44÷184≈39.719≈39.72(万人次).
(三)课堂练习(出示课件17-31)
1.5月18 日,新华社电讯:我国利用世界唯一的“蓝鲸1号”,在南海实现了可燃冰(即天然气水合物)的安全可控开采.据介绍,“蓝鲸1号”拥有27354台设备,约40000根管路,约50 000个MCC报验点,电缆拉放长度估计1200千米.其中准确数是( )
A.27354 B.40000 C.50000 D.1200
2. 近似数5.0×102精确到( )
A.十分位 B.个位 C.十位 D.百位
3.用四舍五入法按要求取近似值:
(1)75 436(精确到百位)
(2)0.785(精确到百分位)
4.下列数据精确到什么位?
(1)小王的身高1.53米;
(2)月球与地球相距38万千米;
(3)圆周率π取3.14159.
5.判断下列说法是否正确,说明理由.
(1)近似数4.60与4.6的精确度相同.
(2)近似数5千万与近似数5000万的精确度相同.
(3)近似4.31万精确到0.01.
(4)1.45×104 精确到0.01.
6.某校七年级共有学生112名,想租用45座的客车外出参观,应租几辆客车?
7.若2m布可做1件衣服,则9m能做多少件这样的衣服?
参考答案:
1.A
2.C
3.解:(1)75 436≈7.54×104 ;(2)0.785≈0.79
4.解:(1)精确到0.01;(2)精确到万位;(3)精确到0.00001
5.解:(1)错,近似数4.60精确到0.01,近似数4.6精确到0.1.
(2)错,近似数5千万精确到千万位,近似数5000万精确到万位.
(3)错,近似数4.31万写成单位为‘个’位的数是43100,数字1所在的位置为百位,故4.31万精确到百位.
(4)错,1.45×104 写成原数为14500,数字5所在位置为百位,故1.45×104精确到百位.
6.解:112÷45=2.488… ≈3(辆).
7.解:9÷2=4.5≈4(件).
(四)课堂小结
今天我们学了哪些内容:
正确理解和掌握近似数、准确实的概念,给出一个近似数,能准确地确定它精确到哪一位,并能按要求求一个数的近似数.
(五)课前预习
预习下节课(2.1)54页到55页的相关内容。
知道用字母表示数和含有字母的式子表示实际问题中的数量关系
七、课后作业
1、教材46页练习
2、下列是由四舍五入法得到的近似数,各精确到哪一位?保留几个有效数字?
(1)132.4; (2)0.0572; (3)2.40万; (4)3000.
八、板书设计:
1.判断准确数与近似数
2.按照要求取近似数.
四舍五入到某一位,就说这个数的近似数精确到那一位.
3.由近似数判断精确度.
九、教学反思:
1.本节课以学生课前收集的生活数据引,使学生获得了直观的体验,认识到数学来源于生活,认识到生活中存在着准确数和近似数,在了解近似数以后,启发学生“生活中还有什么地方用到近似数?”并通过教师自己设计的情境使学生认识到有时是因为客观条件无法或难以得到准确数据,有时是实际问题无需得到准确数据。
2.补充例题以生活实际为背景,不过数据有些大,学生容易出错,教师要提醒学生注意。
3.鼓励学生去查资料,收集资料,培养数感。当数据较大或较小时,适宜 用科学记数法表示,鼓励学生观察生活中的数据,养成良好的数学学习习惯,同时使学生能深深地体会到我们生活在数的世界中。
