2021-2022学年人教版八年级数学下册 18.1.1平行四边形的性质 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册 18.1.1平行四边形的性质 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 11:29:26 | ||
图片预览



文档简介
(共16张PPT)
18.1平行四边形的性质
教材分析
这节内容通过拼图引出平行四边形的定义,让学生经历探索、探究研究、讨论的过程,对平行四边形的概念及性质有本质性的理解,同时通过自己动手操作发现平行四边形的很多性质,教师在教学过程中,结合具体的背景适时的提出问题,满足学生多样化的要求,这节内容对以后的菱形、矩形内容的引入埋下伏笔。
【教学目标】
1.掌握平行四边形的概念。
2.探索并掌握平行四边形的性质,并能运用这些知识进行有关的证明和计算。
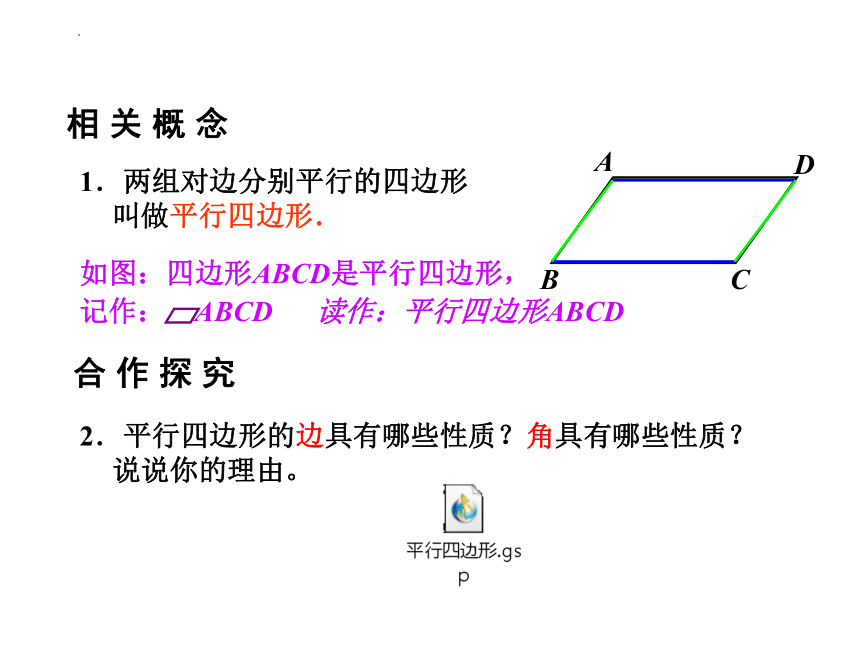
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作: ABCD 读作:平行四边形ABCD
2.平行四边形的边具有哪些性质?角具有哪些性质?说说你的理由。
相 关 概 念
A
D
C
B
合 作 探 究
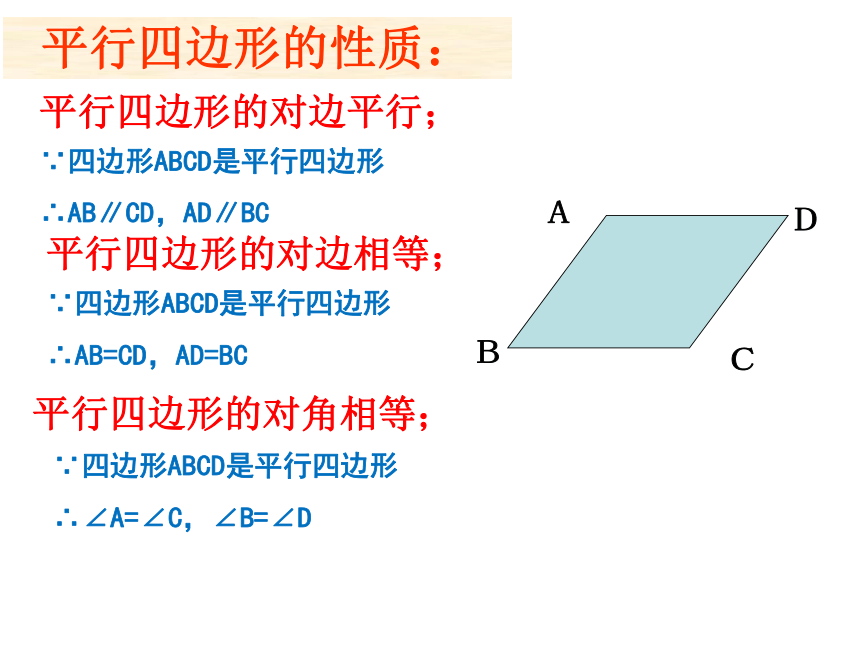
平行四边形的性质:
平行四边形的对边相等;
A
B
C
D
平行四边形的对角相等;
平行四边形的对边平行;
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
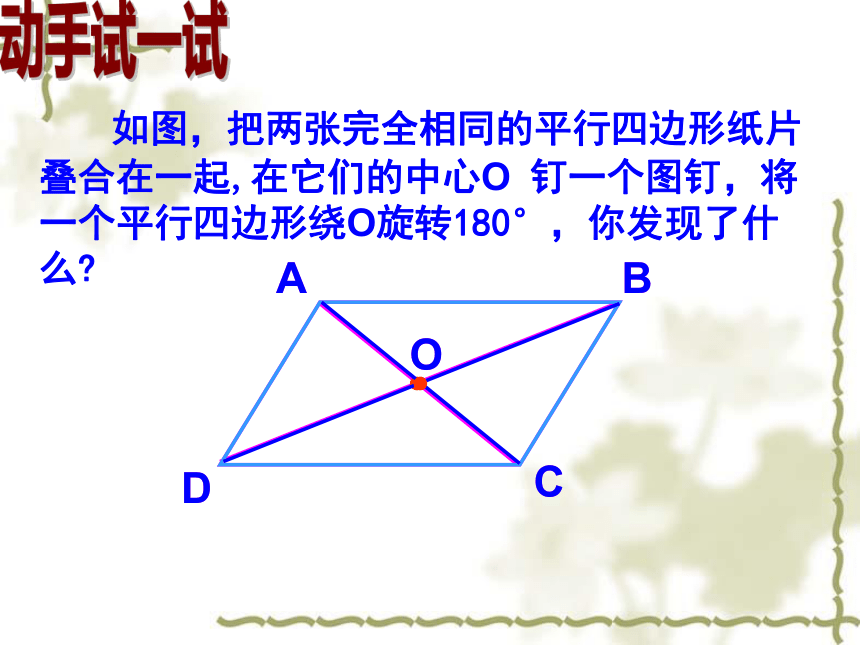
动手试一试
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么
●
A
D
O
C
B
D
B
O
C
A
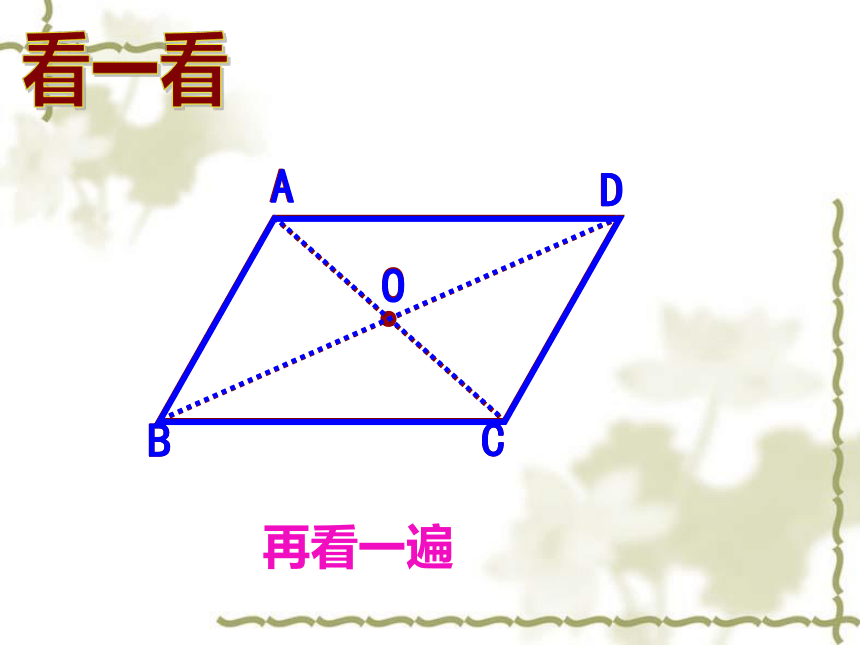
再看一遍
看一看
●
A
D
O
C
B
D
B
O
C
A
看一看
你有什么猜想?
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
证一证
平行四边形的性质:
几何语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
平行四边形的对角线互相平分.
1.如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证AE=CF.
2.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长及□ABCD的面积.
D
C
A
O
8
10
B
运用新知
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵AC⊥BC
∴△ABC是直角三角形
又∵OA=OC ∴
∴S = BC×AC=8×6=48
∵四边形ABCD是平行四边形
∴∠A=∠C,AD=CB
又∵∠AED=∠CAB=90°
∴△ADE≌△CBF
∴AE=CF
3.如图,在□ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( ) 。
4.如图,□ABCD的对角线AC,BD相交于O点,且AC+BD=16,CD=6,。求△ABO的周长。
巩固提升
32°
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO,AB=CD=6
∵AC+BD=16
∴AO+BO=8
∴△ABO的周长=AO+BO+AB=8+6=14
5.〖河北中考〗如图,将□ABCD沿对角线AC折叠,使点B落在点B'处。若∠1=∠2=44°,则∠B的度数的是( )
A 66° B 104° C 114° D 124°
6.〖菏泽中考〗如图,E是□ABCD的边AD的中点,连接CE并延长交BA的延长线于点F,若CD=6,求BF的长。
链接中考
C
∵E是 ABCD的边AD的中点,∴AE=DE.
∵四边形ABCD是平行四边形 ∴AB=CD=6,AB∥CD。∴∠F=∠DCE。
∴又∠AEF=∠DCE,∴△AEF=△DCE ∴AF=CD=6 ∴BF=AB+AF=12
你来评一评
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
A
C
D
B
O
●
老大
老四
老三
老二
M
老人分地合理吗?
故四人的土地面积相同,老人分地合理。
18.1平行四边形的性质
教材分析
这节内容通过拼图引出平行四边形的定义,让学生经历探索、探究研究、讨论的过程,对平行四边形的概念及性质有本质性的理解,同时通过自己动手操作发现平行四边形的很多性质,教师在教学过程中,结合具体的背景适时的提出问题,满足学生多样化的要求,这节内容对以后的菱形、矩形内容的引入埋下伏笔。
【教学目标】
1.掌握平行四边形的概念。
2.探索并掌握平行四边形的性质,并能运用这些知识进行有关的证明和计算。
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作: ABCD 读作:平行四边形ABCD
2.平行四边形的边具有哪些性质?角具有哪些性质?说说你的理由。
相 关 概 念
A
D
C
B
合 作 探 究
平行四边形的性质:
平行四边形的对边相等;
A
B
C
D
平行四边形的对角相等;
平行四边形的对边平行;
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
动手试一试
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么
●
A
D
O
C
B
D
B
O
C
A
再看一遍
看一看
●
A
D
O
C
B
D
B
O
C
A
看一看
你有什么猜想?
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
证一证
平行四边形的性质:
几何语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
平行四边形的对角线互相平分.
1.如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证AE=CF.
2.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长及□ABCD的面积.
D
C
A
O
8
10
B
运用新知
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵AC⊥BC
∴△ABC是直角三角形
又∵OA=OC ∴
∴S = BC×AC=8×6=48
∵四边形ABCD是平行四边形
∴∠A=∠C,AD=CB
又∵∠AED=∠CAB=90°
∴△ADE≌△CBF
∴AE=CF
3.如图,在□ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( ) 。
4.如图,□ABCD的对角线AC,BD相交于O点,且AC+BD=16,CD=6,。求△ABO的周长。
巩固提升
32°
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO,AB=CD=6
∵AC+BD=16
∴AO+BO=8
∴△ABO的周长=AO+BO+AB=8+6=14
5.〖河北中考〗如图,将□ABCD沿对角线AC折叠,使点B落在点B'处。若∠1=∠2=44°,则∠B的度数的是( )
A 66° B 104° C 114° D 124°
6.〖菏泽中考〗如图,E是□ABCD的边AD的中点,连接CE并延长交BA的延长线于点F,若CD=6,求BF的长。
链接中考
C
∵E是 ABCD的边AD的中点,∴AE=DE.
∵四边形ABCD是平行四边形 ∴AB=CD=6,AB∥CD。∴∠F=∠DCE。
∴又∠AEF=∠DCE,∴△AEF=△DCE ∴AF=CD=6 ∴BF=AB+AF=12
你来评一评
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
A
C
D
B
O
●
老大
老四
老三
老二
M
老人分地合理吗?
故四人的土地面积相同,老人分地合理。
