六年级下册数学课件-圆柱圆锥体积人教版((共25张PPT))
文档属性
| 名称 | 六年级下册数学课件-圆柱圆锥体积人教版((共25张PPT)) |  | |
| 格式 | ppt | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 22:42:11 | ||
图片预览






文档简介
(共25张PPT)
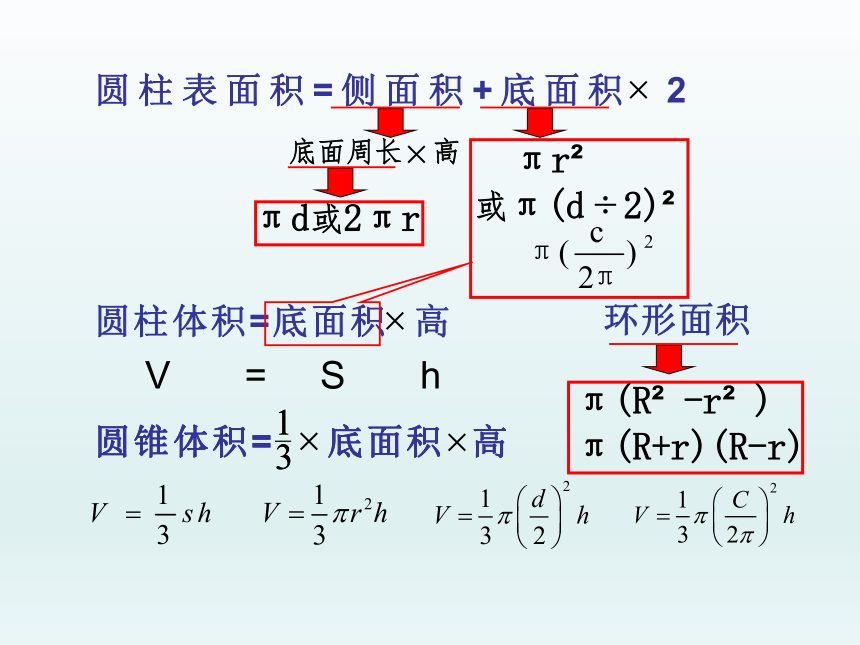
等底等高
1
3
圆锥
体积:
圆柱
体积:
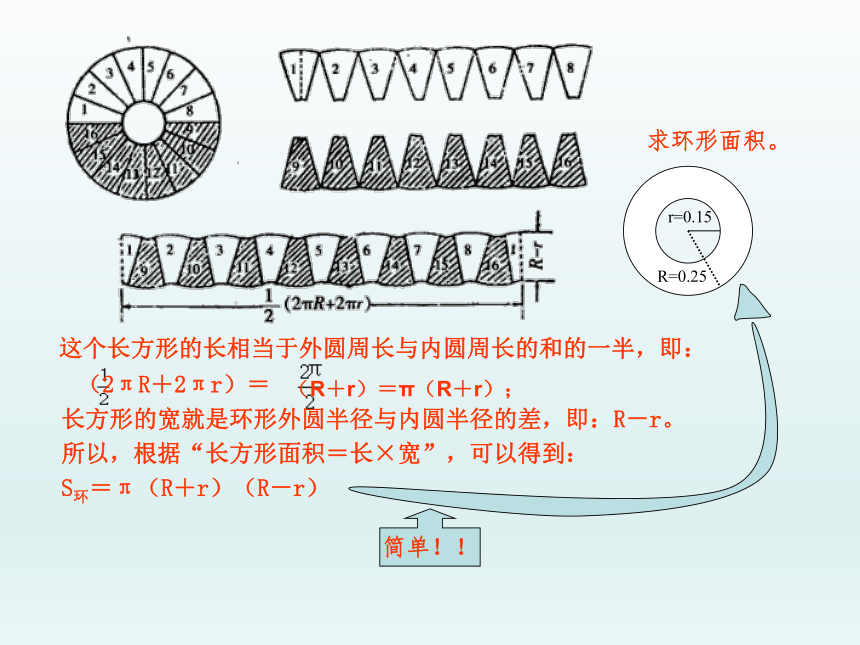
圆柱表面积=侧面积+底面积 2
底面周长 高
πr
或π(d 2)
πd或2πr
圆柱体积=底面积 高
V = S h
环形面积
π(R -r )
π(R+r)(R-r)
圆锥体积= 底面积 高
圆锥体积= 底面积 高
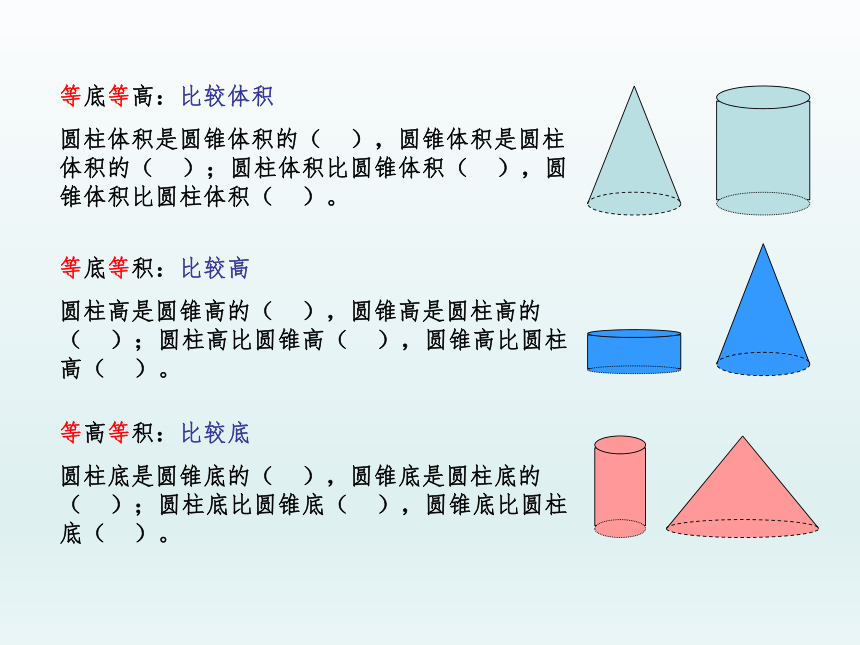
这个长方形的长相当于外圆周长与内圆周长的和的一半,即:
(2πR+2πr)=
长方形的宽就是环形外圆半径与内圆半径的差,即:R-r。
所以,根据“长方形面积=长×宽”,可以得到:
S环=π(R+r)(R-r)
(R+r)=π(R+r);
r=0.15
R=0.25
求环形面积。
简单!!
等底等高:比较体积
圆柱体积是圆锥体积的( ),圆锥体积是圆柱体积的( );圆柱体积比圆锥体积( ),圆锥体积比圆柱体积( )。
等底等积:比较高
圆柱高是圆锥高的( ),圆锥高是圆柱高的( );圆柱高比圆锥高( ),圆锥高比圆柱高( )。
等高等积:比较底
圆柱底是圆锥底的( ),圆锥底是圆柱底的( );圆柱底比圆锥底( ),圆锥底比圆柱底( )。
口答下列各题。
⑷ 把一个圆柱切削成一个最大的圆锥,已知削去部分的体积比圆锥体积大3.6立方分米,那么圆锥的体积是( )立方分米。
⑸ 一个圆锥和一个圆柱等底等高,它们的体积之和是 120 立方分米,这个 圆柱的体积是( )立方分米;圆锥体积比圆柱少( )立方分米。
⑴ 一个圆柱的体积是 300 立方厘米,与它等底等高的圆锥的体积是( )立方厘米。
⑵ 一个圆锥的体积 是 90 立方厘米,与它等底等高的圆柱的体积是( )立方厘米。
⑶ 一个圆柱的体积是 60 立方分米,比与它等底等高的圆锥的体积多( )立方分米。
100
270
40
3.6
90
60
口答下列各题。
⑴ 一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是 9 分米,圆锥的高是 ( )分米。
⑵ 一个圆锥与一个圆柱等底等积,圆锥的高是 24 厘米,圆柱的高比圆锥矮 ( ) 厘米。
⑶ 如果圆柱与圆锥等积等底,它们高的相差 12 厘米,则圆柱的高是 ( )厘米;它们高的和是 ( )厘米。
27
16
6
24
⑴ 一个圆锥与一个圆柱的高相等,体积也相等,圆锥的底面积是90平方厘米, 圆柱的底面积是 ( )平方厘米。
⑵ 一个圆柱与一个圆锥等高等积,圆锥的底面积比圆柱多15 平方分米, 圆柱的底面积是 ( ) 平方分米。
⑶ 一个圆柱与一个圆锥等积等高,如果圆柱的底面积是60平方厘米,则它们的的底面积之和是( )平方厘米。
30
7.5
240
⑷ 一个圆柱与一个圆锥等底等高,如果要使它们的体积相等,则圆锥的高要 ( ) ,或者把圆柱的高 ( );也可以把圆锥的底面积( ) ,或者把圆柱的底面积( )。
扩大3 倍
缩小3 倍
扩大3 倍
缩小3 倍
口答下列各题。
(4)圆柱体的底面直径是3厘米,高是9.42厘米,它的侧面展开后是一个正方形。( )
分析:此题不能只考虑数据,它没有说明如何展开,应该说沿高剪开。
(1)一个圆锥体底面积不变,高扩大6倍,体积也扩大6倍。( )
(2)体积相等的圆柱和圆锥,圆柱的底面积是圆锥底面积的1/3, 所以它们的高相等。( )
(3)如果圆锥的体积是圆柱的 ,那么它们一定等底等高。( )
3
1
(5)底面半径是6厘米的圆锥体的体积等于底面半径是2厘米的等高圆柱的体积。 ( )
2、一个高为30厘米的圆锥容器盛满水,倒入和它等底的圆柱体容器中,水的高度为()。
1、一个圆锥体的高是1.5米,和它等底等体积的圆柱的高是( )。
3、等底等高的一个圆柱和一个圆锥,体积和是72cm ,那么圆锥的体积是( )。如果圆锥的底面积是9cm ,则它的高是( )。
4、一个圆锥体的体积比与它等底等高的圆柱体体积少40立方厘米,这个圆锥体的体积是( )。
分析:以上两题考查的都是圆柱和圆锥的体积关系。1题中要看准等底等体积,即
即 圆锥高1.5,则圆柱高0.5 。既然可以看出等底等体积
柱
锥
sh
sh
3
1
=
柱
锥
h
h
3
1
=
3
1
的情况下,圆柱高是圆锥的 ,所以圆锥盛满水倒入等底的圆柱中,圆柱的高就是10 。
分析:这俩题还是考体积关系。等底等高,则圆锥是1份,圆柱是3份,和是72,则圆锥是18,圆柱是54,既然等底等高,则圆柱底也是9,则高6,则圆锥的高也是6 。4题,圆锥比圆柱少2份,而圆锥相当1份,故40÷2即是。
5、一个圆柱体和一个圆锥体的底面积相等,圆锥的体积是圆柱体的2倍,圆锥的高是24厘米,圆柱体的高是( )厘米。
7、一个圆锥体和一个圆柱体的高相等,它们底面积的比是4:1,圆柱体积是24立方分米,圆锥的体积是( )立方分米。
6、一个圆锥和一个圆柱体的体积相等,圆柱的底面积是圆锥的2倍,圆锥的高是24厘米,圆柱的高是( )厘米。
8、一个圆锥体和一个圆柱体的高的比是2:3,它们底面积的也是2:3,则它们体积的比是( )。
9、把一个直径4厘米、高10厘米的圆柱体沿底面直径平均分成若干份,然后把圆柱切开拼成一个与它等底等高的长方体。这个长方体的表面积增加了( )平方厘米.
10、一个圆柱的底面半径和高是4厘米,如果沿高和底面直径把这个圆柱切成大小相等的两部分,表面积增加( )平方厘米。
3、圆柱的底面积缩小3倍,高扩大2倍,它的体积就( )
A.扩大6倍 B.缩小6倍 C.缩小1.5倍
1、一个圆柱体的底面半径扩大2倍,高扩大5倍,它的底面直径扩大( )倍,周长扩大( )倍,底面积( )倍,侧面积( )倍,体积( )倍。
2
2
4
10
20
注意:公式里边用到的东西,扩大就乘,缩小就除。如上面的1、2俩题。但要注意涉及到半径和直径的时候是倍数的平方。
4、圆锥的高不变,底面半径扩大2倍,它的体积就扩大____倍。
5、圆柱的直径扩大3倍,要使体积不变,高应______。
2、圆柱的体积不变,底面积扩大2倍,高就( )
A、扩大2倍 B、缩小2倍 C、扩大4倍
1、一个圆柱和一个圆锥的体积相等,它们不可能( )
A、等底不等高 B、等高不等底
C、等底等高 D、不等底不等高
2、把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A、50.24 B、100.48 C、64
注意:此题不用计算,正方体的体积是64,最大的圆柱只能小于正方体的体积。
如图,两段圆木的体积之差是314立方厘米。若将它们分别加工成底面是最大正方形的长方体,则两个长方体体积之差是多少立方厘米?
讨论:
正方体木块,和用它削成的最大的圆柱和圆锥体的体积关系。
正方体体积:a
最大的圆柱的体积: a
最大的圆锥体积: a
π
4
π
12
注意上学期学习的正方形与外接圆的关系,圆是π,正方形是2 。
在仓库一角有一堆谷子,量得底面半径为2米,谷堆的高为1米,已知每立方米谷子重720千克,求这堆谷子约重多少千克?
如图,有一个下面是圆柱,上面是圆锥的容器,圆柱的高是10厘米,圆柱的底面直径是8厘米,圆锥的高是6厘米,容器内液面的高是7厘米。当将这个容器倒过来放时,从圆锥的尖到液面的高是多少厘米?
2、有一个直角三角形两条直角边分别是6厘米和4厘米,以其中一条直角边为轴旋转,得到图形的最大体积是多少?
1、将一张长20厘米,宽15厘米的长方形以一条边为轴,旋转一周,能得到的图形的最大体积是多少?
4.如图,直角梯形ABCD,以AB为旋
转轴旋转一周,所以成几何图形的体积
是多少
A
D
B
C
6
4
3
A
D
B
C
6
4
3
2
3
注意:两种情况需要比较一下:3.14×4 ×12和3.14×5 ×8,长宽高差的少的时候要特别注意。
单位:厘米。求瓶子的容积。
单位:厘米。已知求瓶子的容积是1000毫升,求瓶中酒的体积。
20
5
分析:正放和倒放酒的体积不变,那么瓶子倒过来以后上面空着的部分正好是10厘米,正好也是正着时酒的体积,所以:
酒瓶的体积=正放时酒的体积×2
分析:正放和倒放酒的体积不变,瓶子倒过来以后上面空着的部分是5厘米,说明正放时上面空的部分相当于高5厘米的圆柱,就是说这个瓶子相当于高20+5的圆柱。那么:
酒与空着的部分的比就是20:5即4:1 。
一个高度为30厘米,底面直径为2分米的圆锥体容器内盛满水,将水倒入底面直径是4分米的圆柱体容器,此时水的高度是多少厘米?
注意解题步骤:
1、第一遍念题,大致了解情况,单位不同先统一,一般把大单位化成小单位;
2、从问题入手,第二遍念题,找出关系,确定解题方向;
3、具体解答,最好写成分数形式,为了部分明显,容易约分;如上题。
4、解答,要有主要步骤。
解:水的体积不变。2分米=20厘米,4分米=40厘米
3.14×(20÷2)2×30×
3.14×(40÷2)2
答:-----------------------------
= =2.5(厘米)
10×10×10
20×20
如图所示,一个底面直径为20厘米的装有水的圆柱体容器,水中浸没着一个底面直径为12厘米、高为15厘米的圆锥体铅锤,当铅锤从水中取出后,容器中的水下降了多少厘米?
解:下降的水的体积=铅锤的体积
铅垂的体积除以圆柱的底面积即为水下降的深度。
答:-----------------------------------------
写成分数形式约分还是很简便的。
一个装满稻谷的粮囤,上面是圆锥形,下面是
圆柱形,量得圆柱底面的周长是62.8米,高是
2米,圆锥的高是1.2米。这个粮囤能装稻谷多少
立方米?如果每立方米稻谷重500千克,这个粮
囤能装稻谷多少吨?
解:圆柱的底面半径为:62.8÷3.14÷2=10(m)
3.14×10 ×2+3.14×10 ×1.2÷3=628+125.6=753.6(m )
圆柱体积
圆锥体积
753.6×500=376800(千克)=376.8(吨)
答:————————————。
注意有周长求半径的先算出半径来。
一个圆柱体底面周长和高相等,如果高缩短了2厘米,表面积就减少12.56平方厘米。求这个圆柱体的体积。
解题的关键在于求出底周长,如图:高缩短2厘米,表面积就减少12.56平方厘米,用右图表示,从图中不难看出阴影部分就是圆柱体表面积减少部分。
如图,将三角形以斜边为轴旋转一周,计算所得立体图形的体积。(单位:厘米)
一只装有水的长方体玻璃杯,底面积是60平方厘米,水深8厘米。现将一个底面积是12平方厘米的圆柱体铁块竖放在水中后,仍有一部分铁块露在水面上,现在水深多少厘米?
如图,一块长方形铁皮,利用图中的阴影部分刚好能做一个圆柱形油桶(接头处不计),求这个油桶的容积?
一个圆柱的表面积是150.72平方厘米,底面半径是2厘米,求它的体积。
一个圆柱的侧面积是942平方厘米,体积是2355立方厘米,它的底面积是多少平方厘米?
一个圆柱体水桶,底面半径为20厘米,里面盛有80厘米深的水,现将一个底面周长为62.8厘米的圆锥体铁块完全沉入水桶里,水比原来上升了1/16。问圆锥体铁块的高是多少厘米?
一个圆柱体,已知高度每增加1厘米,它的侧面积就增加31.4平方厘米,如果高是16厘米,则它的体积是多少立方厘米?
①这个水池占地面积是多少
③在池内四周和池底抹一层水泥,水泥面的面积是多少平方米
②挖成这个水池,共需挖土多少立方米
一个圆柱形水池,直径是20米,深2米.
有一个圆柱体,它的底面积与侧面积正好相等,如果这个圆柱的底面积不变,高增加3厘米,它的表面积就增加1130.4平方厘米,求原来圆柱体的表面积。
小强为了测一个圆锥形铁块的体积,他将这个铁块浸没在一个底面直径是16厘米,水深10厘米的圆柱形容器中,发现水面上升了,此时水深13厘米。你知道这个铁块的体积吗?
一只圆柱形玻璃杯,内底面直径是8厘米,内装药水的深度是16厘米,恰好占整杯容量的4/5 。这只玻璃杯的深度是多少厘米?(学了比例后更简单。)
有甲、乙两个圆柱形容器,甲容器的底面积是690平方厘米,乙容器的底面积是230平方厘米,甲容器中的水深36厘米,现将其中一部分水倒入空着的乙容器中,使甲、乙容器内的水深一样,则甲、乙容器中水深多少厘米?
用直径为40厘米的圆钢锻造长3米、宽10分米、厚2厘米的长方形钢板,应截取多长的一段圆钢?
一个圆柱与一个圆锥的体积相等,圆柱的高与圆锥的高之比是4:9,圆锥的底面积是20平方厘米,圆柱的底面积是多少平方厘米?
一个圆柱和一个圆锥的体积相等,圆锥高是圆柱高的三分之二,求圆锥和圆柱的底面积比是多少?
一个圆柱的底面周长是18.84厘米,沿着底面直径将它切成相等的两半,表面积增加了180平方厘米,原来这个圆柱的表面积和体积各是多少?
A、B两个圆柱形容器,底面积之比为5:3,A容器水深20厘米,B容器水深10厘米,再往两个容器里注入同样多的水,使得两个容器中的水深相等,这时水深多少厘米?
把一个圆锥沿底面直径平均分成体积相等、形状相同的两部分,表面积比原来增加了120平方厘米。圆锥高10厘米,圆锥的体积是多少立方厘米?
甲乙两个圆柱形容器,从里面量得它们的半径分别是10厘米和5厘米,两个容器内分别盛有10厘米和15厘米的水,现将乙容器中的一部分水倒入甲容器内,使得两个容器内的水面相平,这时水深为多少厘米?
自来水管的内半径是2cm,管内水的流速是每秒20cm。一位同学打开水龙头洗手,走时忘了关,5分钟后被另一名同学发现才关上,请你算一算,大约浪费了多少升水
等底等高
1
3
圆锥
体积:
圆柱
体积:
圆柱表面积=侧面积+底面积 2
底面周长 高
πr
或π(d 2)
πd或2πr
圆柱体积=底面积 高
V = S h
环形面积
π(R -r )
π(R+r)(R-r)
圆锥体积= 底面积 高
圆锥体积= 底面积 高
这个长方形的长相当于外圆周长与内圆周长的和的一半,即:
(2πR+2πr)=
长方形的宽就是环形外圆半径与内圆半径的差,即:R-r。
所以,根据“长方形面积=长×宽”,可以得到:
S环=π(R+r)(R-r)
(R+r)=π(R+r);
r=0.15
R=0.25
求环形面积。
简单!!
等底等高:比较体积
圆柱体积是圆锥体积的( ),圆锥体积是圆柱体积的( );圆柱体积比圆锥体积( ),圆锥体积比圆柱体积( )。
等底等积:比较高
圆柱高是圆锥高的( ),圆锥高是圆柱高的( );圆柱高比圆锥高( ),圆锥高比圆柱高( )。
等高等积:比较底
圆柱底是圆锥底的( ),圆锥底是圆柱底的( );圆柱底比圆锥底( ),圆锥底比圆柱底( )。
口答下列各题。
⑷ 把一个圆柱切削成一个最大的圆锥,已知削去部分的体积比圆锥体积大3.6立方分米,那么圆锥的体积是( )立方分米。
⑸ 一个圆锥和一个圆柱等底等高,它们的体积之和是 120 立方分米,这个 圆柱的体积是( )立方分米;圆锥体积比圆柱少( )立方分米。
⑴ 一个圆柱的体积是 300 立方厘米,与它等底等高的圆锥的体积是( )立方厘米。
⑵ 一个圆锥的体积 是 90 立方厘米,与它等底等高的圆柱的体积是( )立方厘米。
⑶ 一个圆柱的体积是 60 立方分米,比与它等底等高的圆锥的体积多( )立方分米。
100
270
40
3.6
90
60
口答下列各题。
⑴ 一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是 9 分米,圆锥的高是 ( )分米。
⑵ 一个圆锥与一个圆柱等底等积,圆锥的高是 24 厘米,圆柱的高比圆锥矮 ( ) 厘米。
⑶ 如果圆柱与圆锥等积等底,它们高的相差 12 厘米,则圆柱的高是 ( )厘米;它们高的和是 ( )厘米。
27
16
6
24
⑴ 一个圆锥与一个圆柱的高相等,体积也相等,圆锥的底面积是90平方厘米, 圆柱的底面积是 ( )平方厘米。
⑵ 一个圆柱与一个圆锥等高等积,圆锥的底面积比圆柱多15 平方分米, 圆柱的底面积是 ( ) 平方分米。
⑶ 一个圆柱与一个圆锥等积等高,如果圆柱的底面积是60平方厘米,则它们的的底面积之和是( )平方厘米。
30
7.5
240
⑷ 一个圆柱与一个圆锥等底等高,如果要使它们的体积相等,则圆锥的高要 ( ) ,或者把圆柱的高 ( );也可以把圆锥的底面积( ) ,或者把圆柱的底面积( )。
扩大3 倍
缩小3 倍
扩大3 倍
缩小3 倍
口答下列各题。
(4)圆柱体的底面直径是3厘米,高是9.42厘米,它的侧面展开后是一个正方形。( )
分析:此题不能只考虑数据,它没有说明如何展开,应该说沿高剪开。
(1)一个圆锥体底面积不变,高扩大6倍,体积也扩大6倍。( )
(2)体积相等的圆柱和圆锥,圆柱的底面积是圆锥底面积的1/3, 所以它们的高相等。( )
(3)如果圆锥的体积是圆柱的 ,那么它们一定等底等高。( )
3
1
(5)底面半径是6厘米的圆锥体的体积等于底面半径是2厘米的等高圆柱的体积。 ( )
2、一个高为30厘米的圆锥容器盛满水,倒入和它等底的圆柱体容器中,水的高度为()。
1、一个圆锥体的高是1.5米,和它等底等体积的圆柱的高是( )。
3、等底等高的一个圆柱和一个圆锥,体积和是72cm ,那么圆锥的体积是( )。如果圆锥的底面积是9cm ,则它的高是( )。
4、一个圆锥体的体积比与它等底等高的圆柱体体积少40立方厘米,这个圆锥体的体积是( )。
分析:以上两题考查的都是圆柱和圆锥的体积关系。1题中要看准等底等体积,即
即 圆锥高1.5,则圆柱高0.5 。既然可以看出等底等体积
柱
锥
sh
sh
3
1
=
柱
锥
h
h
3
1
=
3
1
的情况下,圆柱高是圆锥的 ,所以圆锥盛满水倒入等底的圆柱中,圆柱的高就是10 。
分析:这俩题还是考体积关系。等底等高,则圆锥是1份,圆柱是3份,和是72,则圆锥是18,圆柱是54,既然等底等高,则圆柱底也是9,则高6,则圆锥的高也是6 。4题,圆锥比圆柱少2份,而圆锥相当1份,故40÷2即是。
5、一个圆柱体和一个圆锥体的底面积相等,圆锥的体积是圆柱体的2倍,圆锥的高是24厘米,圆柱体的高是( )厘米。
7、一个圆锥体和一个圆柱体的高相等,它们底面积的比是4:1,圆柱体积是24立方分米,圆锥的体积是( )立方分米。
6、一个圆锥和一个圆柱体的体积相等,圆柱的底面积是圆锥的2倍,圆锥的高是24厘米,圆柱的高是( )厘米。
8、一个圆锥体和一个圆柱体的高的比是2:3,它们底面积的也是2:3,则它们体积的比是( )。
9、把一个直径4厘米、高10厘米的圆柱体沿底面直径平均分成若干份,然后把圆柱切开拼成一个与它等底等高的长方体。这个长方体的表面积增加了( )平方厘米.
10、一个圆柱的底面半径和高是4厘米,如果沿高和底面直径把这个圆柱切成大小相等的两部分,表面积增加( )平方厘米。
3、圆柱的底面积缩小3倍,高扩大2倍,它的体积就( )
A.扩大6倍 B.缩小6倍 C.缩小1.5倍
1、一个圆柱体的底面半径扩大2倍,高扩大5倍,它的底面直径扩大( )倍,周长扩大( )倍,底面积( )倍,侧面积( )倍,体积( )倍。
2
2
4
10
20
注意:公式里边用到的东西,扩大就乘,缩小就除。如上面的1、2俩题。但要注意涉及到半径和直径的时候是倍数的平方。
4、圆锥的高不变,底面半径扩大2倍,它的体积就扩大____倍。
5、圆柱的直径扩大3倍,要使体积不变,高应______。
2、圆柱的体积不变,底面积扩大2倍,高就( )
A、扩大2倍 B、缩小2倍 C、扩大4倍
1、一个圆柱和一个圆锥的体积相等,它们不可能( )
A、等底不等高 B、等高不等底
C、等底等高 D、不等底不等高
2、把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A、50.24 B、100.48 C、64
注意:此题不用计算,正方体的体积是64,最大的圆柱只能小于正方体的体积。
如图,两段圆木的体积之差是314立方厘米。若将它们分别加工成底面是最大正方形的长方体,则两个长方体体积之差是多少立方厘米?
讨论:
正方体木块,和用它削成的最大的圆柱和圆锥体的体积关系。
正方体体积:a
最大的圆柱的体积: a
最大的圆锥体积: a
π
4
π
12
注意上学期学习的正方形与外接圆的关系,圆是π,正方形是2 。
在仓库一角有一堆谷子,量得底面半径为2米,谷堆的高为1米,已知每立方米谷子重720千克,求这堆谷子约重多少千克?
如图,有一个下面是圆柱,上面是圆锥的容器,圆柱的高是10厘米,圆柱的底面直径是8厘米,圆锥的高是6厘米,容器内液面的高是7厘米。当将这个容器倒过来放时,从圆锥的尖到液面的高是多少厘米?
2、有一个直角三角形两条直角边分别是6厘米和4厘米,以其中一条直角边为轴旋转,得到图形的最大体积是多少?
1、将一张长20厘米,宽15厘米的长方形以一条边为轴,旋转一周,能得到的图形的最大体积是多少?
4.如图,直角梯形ABCD,以AB为旋
转轴旋转一周,所以成几何图形的体积
是多少
A
D
B
C
6
4
3
A
D
B
C
6
4
3
2
3
注意:两种情况需要比较一下:3.14×4 ×12和3.14×5 ×8,长宽高差的少的时候要特别注意。
单位:厘米。求瓶子的容积。
单位:厘米。已知求瓶子的容积是1000毫升,求瓶中酒的体积。
20
5
分析:正放和倒放酒的体积不变,那么瓶子倒过来以后上面空着的部分正好是10厘米,正好也是正着时酒的体积,所以:
酒瓶的体积=正放时酒的体积×2
分析:正放和倒放酒的体积不变,瓶子倒过来以后上面空着的部分是5厘米,说明正放时上面空的部分相当于高5厘米的圆柱,就是说这个瓶子相当于高20+5的圆柱。那么:
酒与空着的部分的比就是20:5即4:1 。
一个高度为30厘米,底面直径为2分米的圆锥体容器内盛满水,将水倒入底面直径是4分米的圆柱体容器,此时水的高度是多少厘米?
注意解题步骤:
1、第一遍念题,大致了解情况,单位不同先统一,一般把大单位化成小单位;
2、从问题入手,第二遍念题,找出关系,确定解题方向;
3、具体解答,最好写成分数形式,为了部分明显,容易约分;如上题。
4、解答,要有主要步骤。
解:水的体积不变。2分米=20厘米,4分米=40厘米
3.14×(20÷2)2×30×
3.14×(40÷2)2
答:-----------------------------
= =2.5(厘米)
10×10×10
20×20
如图所示,一个底面直径为20厘米的装有水的圆柱体容器,水中浸没着一个底面直径为12厘米、高为15厘米的圆锥体铅锤,当铅锤从水中取出后,容器中的水下降了多少厘米?
解:下降的水的体积=铅锤的体积
铅垂的体积除以圆柱的底面积即为水下降的深度。
答:-----------------------------------------
写成分数形式约分还是很简便的。
一个装满稻谷的粮囤,上面是圆锥形,下面是
圆柱形,量得圆柱底面的周长是62.8米,高是
2米,圆锥的高是1.2米。这个粮囤能装稻谷多少
立方米?如果每立方米稻谷重500千克,这个粮
囤能装稻谷多少吨?
解:圆柱的底面半径为:62.8÷3.14÷2=10(m)
3.14×10 ×2+3.14×10 ×1.2÷3=628+125.6=753.6(m )
圆柱体积
圆锥体积
753.6×500=376800(千克)=376.8(吨)
答:————————————。
注意有周长求半径的先算出半径来。
一个圆柱体底面周长和高相等,如果高缩短了2厘米,表面积就减少12.56平方厘米。求这个圆柱体的体积。
解题的关键在于求出底周长,如图:高缩短2厘米,表面积就减少12.56平方厘米,用右图表示,从图中不难看出阴影部分就是圆柱体表面积减少部分。
如图,将三角形以斜边为轴旋转一周,计算所得立体图形的体积。(单位:厘米)
一只装有水的长方体玻璃杯,底面积是60平方厘米,水深8厘米。现将一个底面积是12平方厘米的圆柱体铁块竖放在水中后,仍有一部分铁块露在水面上,现在水深多少厘米?
如图,一块长方形铁皮,利用图中的阴影部分刚好能做一个圆柱形油桶(接头处不计),求这个油桶的容积?
一个圆柱的表面积是150.72平方厘米,底面半径是2厘米,求它的体积。
一个圆柱的侧面积是942平方厘米,体积是2355立方厘米,它的底面积是多少平方厘米?
一个圆柱体水桶,底面半径为20厘米,里面盛有80厘米深的水,现将一个底面周长为62.8厘米的圆锥体铁块完全沉入水桶里,水比原来上升了1/16。问圆锥体铁块的高是多少厘米?
一个圆柱体,已知高度每增加1厘米,它的侧面积就增加31.4平方厘米,如果高是16厘米,则它的体积是多少立方厘米?
①这个水池占地面积是多少
③在池内四周和池底抹一层水泥,水泥面的面积是多少平方米
②挖成这个水池,共需挖土多少立方米
一个圆柱形水池,直径是20米,深2米.
有一个圆柱体,它的底面积与侧面积正好相等,如果这个圆柱的底面积不变,高增加3厘米,它的表面积就增加1130.4平方厘米,求原来圆柱体的表面积。
小强为了测一个圆锥形铁块的体积,他将这个铁块浸没在一个底面直径是16厘米,水深10厘米的圆柱形容器中,发现水面上升了,此时水深13厘米。你知道这个铁块的体积吗?
一只圆柱形玻璃杯,内底面直径是8厘米,内装药水的深度是16厘米,恰好占整杯容量的4/5 。这只玻璃杯的深度是多少厘米?(学了比例后更简单。)
有甲、乙两个圆柱形容器,甲容器的底面积是690平方厘米,乙容器的底面积是230平方厘米,甲容器中的水深36厘米,现将其中一部分水倒入空着的乙容器中,使甲、乙容器内的水深一样,则甲、乙容器中水深多少厘米?
用直径为40厘米的圆钢锻造长3米、宽10分米、厚2厘米的长方形钢板,应截取多长的一段圆钢?
一个圆柱与一个圆锥的体积相等,圆柱的高与圆锥的高之比是4:9,圆锥的底面积是20平方厘米,圆柱的底面积是多少平方厘米?
一个圆柱和一个圆锥的体积相等,圆锥高是圆柱高的三分之二,求圆锥和圆柱的底面积比是多少?
一个圆柱的底面周长是18.84厘米,沿着底面直径将它切成相等的两半,表面积增加了180平方厘米,原来这个圆柱的表面积和体积各是多少?
A、B两个圆柱形容器,底面积之比为5:3,A容器水深20厘米,B容器水深10厘米,再往两个容器里注入同样多的水,使得两个容器中的水深相等,这时水深多少厘米?
把一个圆锥沿底面直径平均分成体积相等、形状相同的两部分,表面积比原来增加了120平方厘米。圆锥高10厘米,圆锥的体积是多少立方厘米?
甲乙两个圆柱形容器,从里面量得它们的半径分别是10厘米和5厘米,两个容器内分别盛有10厘米和15厘米的水,现将乙容器中的一部分水倒入甲容器内,使得两个容器内的水面相平,这时水深为多少厘米?
自来水管的内半径是2cm,管内水的流速是每秒20cm。一位同学打开水龙头洗手,走时忘了关,5分钟后被另一名同学发现才关上,请你算一算,大约浪费了多少升水
