11.2.2 三角形的外角 课堂同步练(分类练+提升练+拓展练+答案)
文档属性
| 名称 | 11.2.2 三角形的外角 课堂同步练(分类练+提升练+拓展练+答案) | 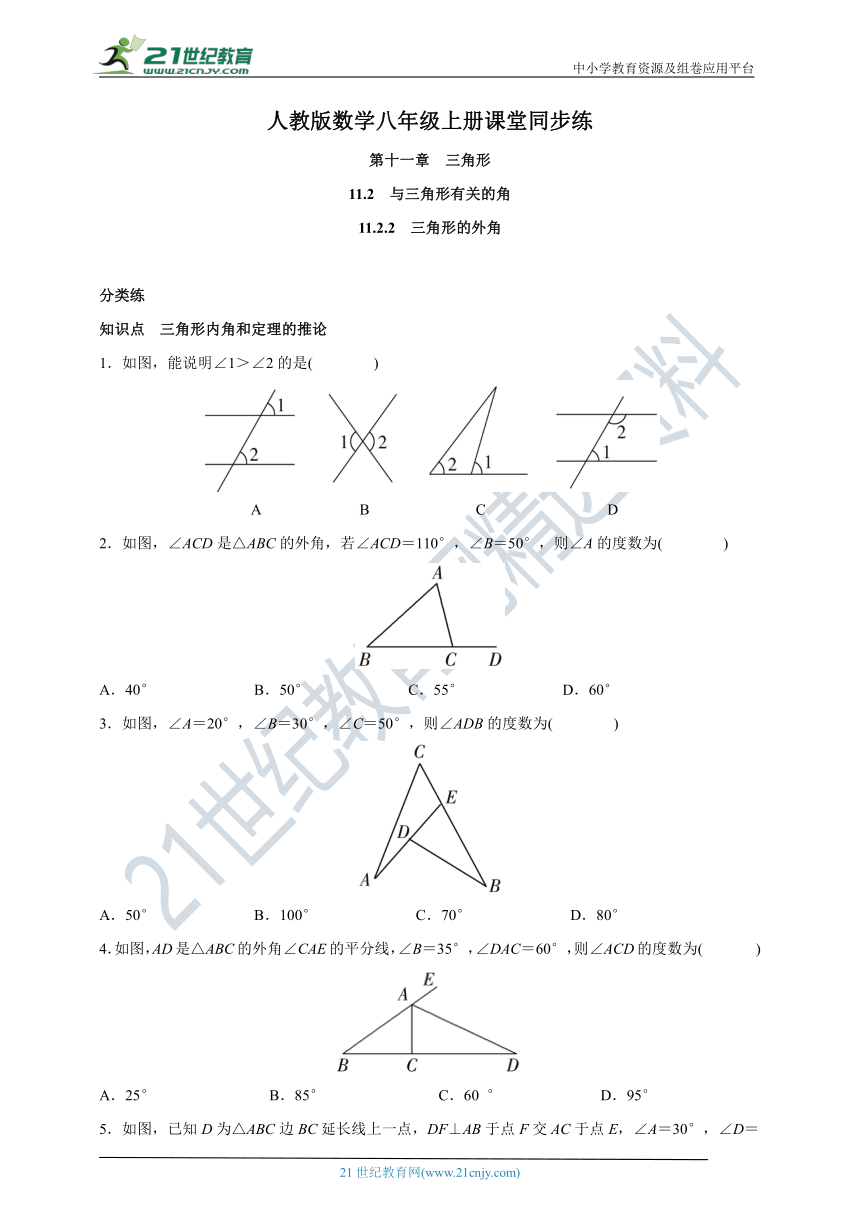 | |
| 格式 | doc | ||
| 文件大小 | 685.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 09:53:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学八年级上册课堂同步练
第十一章 三角形
11.2 与三角形有关的角
11.2.2 三角形的外角
分类练
知识点 三角形内角和定理的推论
1.如图,能说明∠1>∠2的是( )
A B C D
2.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A的度数为( )
A.40° B.50° C.55° D.60°
3.如图,∠A=20°,∠B=30°,∠C=50°,则∠ADB的度数为( )
A.50° B.100° C.70° D.80°
4.如图,AD是△ABC的外角∠CAE的平分线,∠B=35°,∠DAC=60°,则∠ACD的度数为( )
A.25° B.85° C.60 ° D.95°
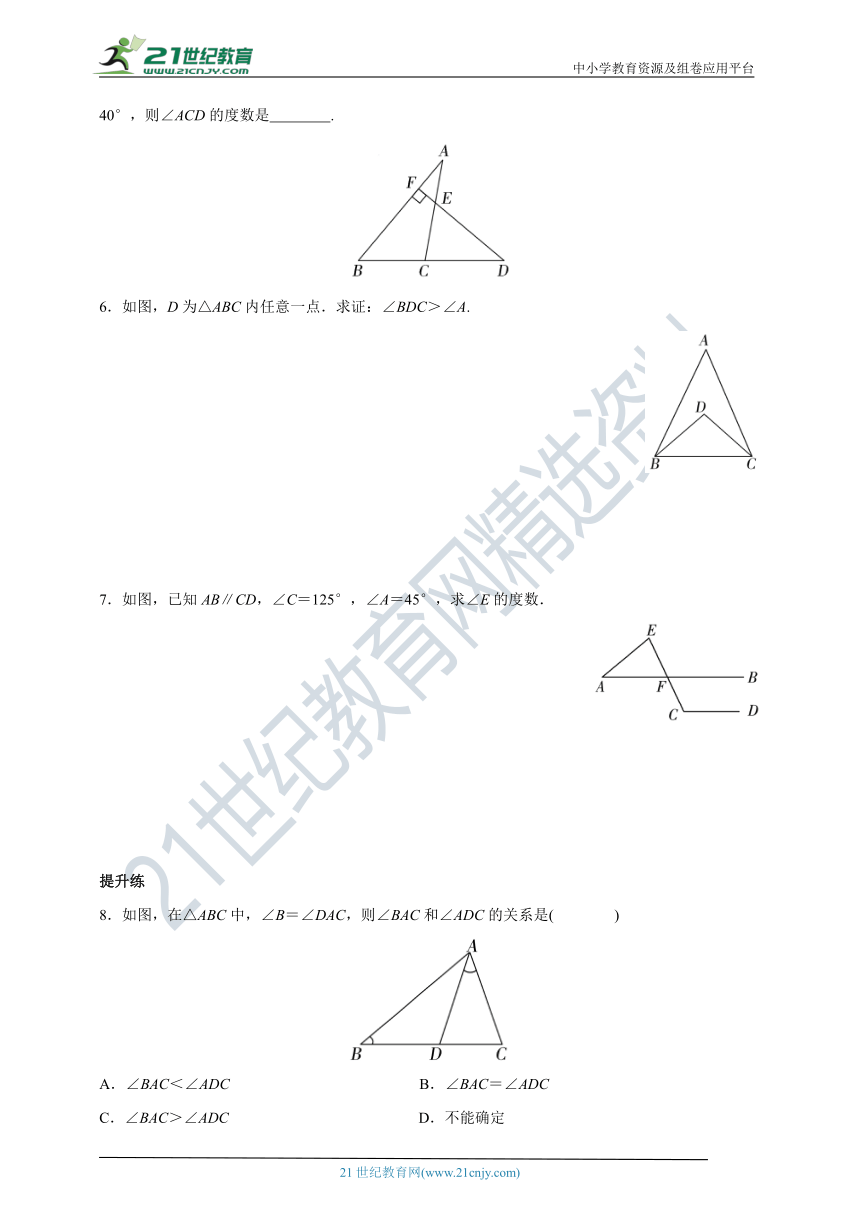
5.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于点F交AC于点E,∠A=30°,∠D=40°,则∠ACD的度数是 .
6.如图,D为△ABC内任意一点.求证:∠BDC>∠A.
7.如图,已知AB∥CD,∠C=125°,∠A=45°,求∠E的度数.
提升练
8.如图,在△ABC中,∠B=∠DAC,则∠BAC和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
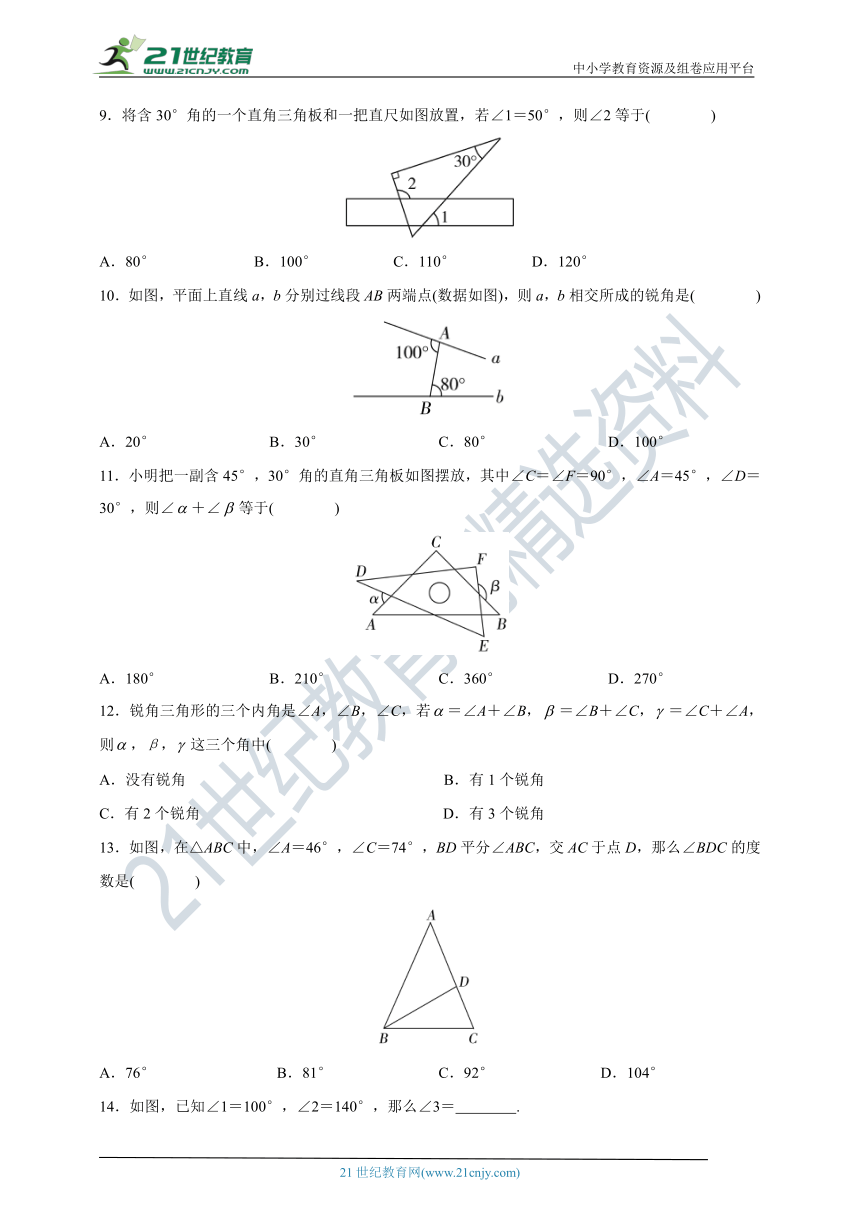
9.将含30°角的一个直角三角板和一把直尺如图放置,若∠1=50°,则∠2等于( )
A.80° B.100° C.110° D.120°
10.如图,平面上直线a,b分别过线段AB两端点(数据如图),则a,b相交所成的锐角是( )
A.20° B.30° C.80° D.100°
11.小明把一副含45°,30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠+∠等于( )
A.180° B.210° C.360° D.270°
12.锐角三角形的三个内角是∠A,∠B,∠C,若=∠A+∠B,=∠B+∠C,=∠C+∠A,则,β,这三个角中( )
A.没有锐角 B.有1个锐角
C.有2个锐角 D.有3个锐角
13.如图,在△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是( )
A.76° B.81° C.92° D.104°
14.如图,已知∠1=100°,∠2=140°,那么∠3= .
15.将一副三角板按如图所示的方式叠放,则= .
16.△ABC的三个内角∠BAC,∠ABC,∠ACB的外角依次记为∠,∠,∠,若∠=2∠ABC,∠-∠=40°,则∠BAC= ,∠ABC= ,∠ACB= .
17.一个零件的形状如图所示,按规定∠BAD,∠B,∠D分别是90°,32°和21°,要测量这个零件是否合格,检验工人需测量∠BCD的度数.如果量得∠BCD=150°,则判定这个零件不合格,你知道这是为什么吗?请说明原因.
18.如图,已知△ABC,在AB延长线上任取一点D,在AC延长线上任取一点E,分别作∠CBD与∠BCE的平分线相交于点P,请你猜想∠P与∠A的关系,并证明你的猜想是正确的.
拓展练
19.如图,在平面直角坐标系xOy中,点A是x轴正半轴上的动点,点B是y轴正半轴上的动点,作射线AB,∠OAB的平分线与∠OBA的外角的平分线交于点C.
(1)当OA=OB时,∠C的度数是________;
(2)当点A,B分别在x轴和y轴正半轴上移动时,∠C的大小是否变化?请说明理由.
参 考 答 案
1.C
2.D
3.B
4.D
5.80°
6.证明:如图,延长BD交AC于点E. ∵∠BDC是△DEC的一个外角,∴∠BDC>∠DEC. 又∵∠DEC是△ABE的一个外角,∴∠DEC>∠A. ∴∠BDC>∠A.
7.解:∵直线AB∥CD,∠C=125°,∴∠EFB=∠C=125°. ∵∠EFB=∠A+∠E,∠A=45°,∴∠E=∠EFB-∠A=125°-45°=80°.
8.B
9.C
10.A
11.B
12.A
13.A
14.60°
15.75°
16.40° 60° 80°
17.解:如图,连接AC并延长.由三角形的外角性质,∠3=∠1+∠B,∠4=∠2+∠D,∴∠BCD=∠3+∠4=∠1+∠B+∠2+∠D=∠BAD+∠B+∠D=90°+32°+21°=143°. ∵143°≠150°,∴这个零件不合格.
18.解:∠P=90°-∠A. 理由:∵∠DBC,∠BCE都是△ABC的外角,∴∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC. ∵BP平分∠CBD,∴∠PBC=∠CBD.∵CP平分∠BCE,∴∠BCP=∠BCE. ∴∠PBC=∠A+∠ACB,∠BCP=∠A+∠ABC.∴∠P=180°-(∠BCP+∠PBC)=180°-(∠A+∠ABC+∠A+∠ACB)=180°-[(∠A+∠ABC+∠ACB)+∠A]=180°-90°-∠A=90°-∠A,即∠P=90°-∠A.
19.解:(1)45° 提示:∵∠AOB=90°,OA=OB,∴∠OAB=∠OBA=45°,∴∠DBO=180°-45°=135°. ∵点C是∠OAB的平分线与∠OBA的外角的平分线的交点,∴∠CAB=∠OAB=22.5°,∴∠CBO=∠DBO=67.5°,∴∠CAB+∠CBO+∠OBA=22.5°+67.5°+45°=135°,∴∠C=180°-(∠CAB+∠CBO+∠OBA)=180°-135°=45°. 故答案为45°.
(2)∠C的大小不变.理由:设∠DBC=α,∠BAC=β,∵BC平分∠DBO,AC平分∠BAO,∴∠CBO=∠DBC=α,∠OAC=∠BAC=β. ∵∠DBO是△AOB的外角,∠DBC是△ABC的外角,∴解得∠C=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级上册课堂同步练
第十一章 三角形
11.2 与三角形有关的角
11.2.2 三角形的外角
分类练
知识点 三角形内角和定理的推论
1.如图,能说明∠1>∠2的是( )
A B C D
2.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A的度数为( )
A.40° B.50° C.55° D.60°
3.如图,∠A=20°,∠B=30°,∠C=50°,则∠ADB的度数为( )
A.50° B.100° C.70° D.80°
4.如图,AD是△ABC的外角∠CAE的平分线,∠B=35°,∠DAC=60°,则∠ACD的度数为( )
A.25° B.85° C.60 ° D.95°
5.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于点F交AC于点E,∠A=30°,∠D=40°,则∠ACD的度数是 .
6.如图,D为△ABC内任意一点.求证:∠BDC>∠A.
7.如图,已知AB∥CD,∠C=125°,∠A=45°,求∠E的度数.
提升练
8.如图,在△ABC中,∠B=∠DAC,则∠BAC和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
9.将含30°角的一个直角三角板和一把直尺如图放置,若∠1=50°,则∠2等于( )
A.80° B.100° C.110° D.120°
10.如图,平面上直线a,b分别过线段AB两端点(数据如图),则a,b相交所成的锐角是( )
A.20° B.30° C.80° D.100°
11.小明把一副含45°,30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠+∠等于( )
A.180° B.210° C.360° D.270°
12.锐角三角形的三个内角是∠A,∠B,∠C,若=∠A+∠B,=∠B+∠C,=∠C+∠A,则,β,这三个角中( )
A.没有锐角 B.有1个锐角
C.有2个锐角 D.有3个锐角
13.如图,在△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是( )
A.76° B.81° C.92° D.104°
14.如图,已知∠1=100°,∠2=140°,那么∠3= .
15.将一副三角板按如图所示的方式叠放,则= .
16.△ABC的三个内角∠BAC,∠ABC,∠ACB的外角依次记为∠,∠,∠,若∠=2∠ABC,∠-∠=40°,则∠BAC= ,∠ABC= ,∠ACB= .
17.一个零件的形状如图所示,按规定∠BAD,∠B,∠D分别是90°,32°和21°,要测量这个零件是否合格,检验工人需测量∠BCD的度数.如果量得∠BCD=150°,则判定这个零件不合格,你知道这是为什么吗?请说明原因.
18.如图,已知△ABC,在AB延长线上任取一点D,在AC延长线上任取一点E,分别作∠CBD与∠BCE的平分线相交于点P,请你猜想∠P与∠A的关系,并证明你的猜想是正确的.
拓展练
19.如图,在平面直角坐标系xOy中,点A是x轴正半轴上的动点,点B是y轴正半轴上的动点,作射线AB,∠OAB的平分线与∠OBA的外角的平分线交于点C.
(1)当OA=OB时,∠C的度数是________;
(2)当点A,B分别在x轴和y轴正半轴上移动时,∠C的大小是否变化?请说明理由.
参 考 答 案
1.C
2.D
3.B
4.D
5.80°
6.证明:如图,延长BD交AC于点E. ∵∠BDC是△DEC的一个外角,∴∠BDC>∠DEC. 又∵∠DEC是△ABE的一个外角,∴∠DEC>∠A. ∴∠BDC>∠A.
7.解:∵直线AB∥CD,∠C=125°,∴∠EFB=∠C=125°. ∵∠EFB=∠A+∠E,∠A=45°,∴∠E=∠EFB-∠A=125°-45°=80°.
8.B
9.C
10.A
11.B
12.A
13.A
14.60°
15.75°
16.40° 60° 80°
17.解:如图,连接AC并延长.由三角形的外角性质,∠3=∠1+∠B,∠4=∠2+∠D,∴∠BCD=∠3+∠4=∠1+∠B+∠2+∠D=∠BAD+∠B+∠D=90°+32°+21°=143°. ∵143°≠150°,∴这个零件不合格.
18.解:∠P=90°-∠A. 理由:∵∠DBC,∠BCE都是△ABC的外角,∴∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC. ∵BP平分∠CBD,∴∠PBC=∠CBD.∵CP平分∠BCE,∴∠BCP=∠BCE. ∴∠PBC=∠A+∠ACB,∠BCP=∠A+∠ABC.∴∠P=180°-(∠BCP+∠PBC)=180°-(∠A+∠ABC+∠A+∠ACB)=180°-[(∠A+∠ABC+∠ACB)+∠A]=180°-90°-∠A=90°-∠A,即∠P=90°-∠A.
19.解:(1)45° 提示:∵∠AOB=90°,OA=OB,∴∠OAB=∠OBA=45°,∴∠DBO=180°-45°=135°. ∵点C是∠OAB的平分线与∠OBA的外角的平分线的交点,∴∠CAB=∠OAB=22.5°,∴∠CBO=∠DBO=67.5°,∴∠CAB+∠CBO+∠OBA=22.5°+67.5°+45°=135°,∴∠C=180°-(∠CAB+∠CBO+∠OBA)=180°-135°=45°. 故答案为45°.
(2)∠C的大小不变.理由:设∠DBC=α,∠BAC=β,∵BC平分∠DBO,AC平分∠BAO,∴∠CBO=∠DBC=α,∠OAC=∠BAC=β. ∵∠DBO是△AOB的外角,∠DBC是△ABC的外角,∴解得∠C=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
