11.3.2 多边形的内角和课堂同步练(分类练+提升练+拓展练+答案)
文档属性
| 名称 | 11.3.2 多边形的内角和课堂同步练(分类练+提升练+拓展练+答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 376.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级上册课堂同步练
第十一章 三角形
11.3 多边形及其内角和
11.3.2 多边形的内角和
分类练
知识点1 多边形的内角和
1.如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为( )
A.120° B.110° C.100° D.40°
2.若一个多边形的内角和为720°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
3.正十边形的每一个内角的度数为( )
A.120° B.135° C.140° D.144°
4.n边形的边每增加一条,它的内角和就增加 .
5.小辉同学在计算某个多边形的内角和时,求得的内角和为1125°,检查发现错误原因是少加了一个内角,求少加的这个内角是多少度?正确的结果应是多少?
知识点2 多边形的外角和
6.一个多边形的每一个外角都等于36°,则这个多边形的边数n等于( )
A.8 B.10 C.12 D.14
7.一个多边形的每个内角都等于135°,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
8.下列多边形中,内角和与外角和相等的是( )
A B C D
9.已知正多边形的一个外角等于40°,则这个正多边形的内角和的度数为 .
10.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数及内角和.
提升练
11.我们在探究“任意一个四边形内角和是多少度”时,采用的方法是连接四边形的一条对角线,把四边形分割成两个三角形,从而探究出任意四边形的内角和等于360°,这一过程体现的数学思想是( )
A.转化思想 B.方程思想 C.函数思想 D.数形结合思想
12.一个三角形,剪去一个角后所得的多边形内角和的度数是( )
A.180° B.360° C.540° D.180°或360°
13.将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.900°
14.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是 ( )
A.180° B.220° C.240° D.300°
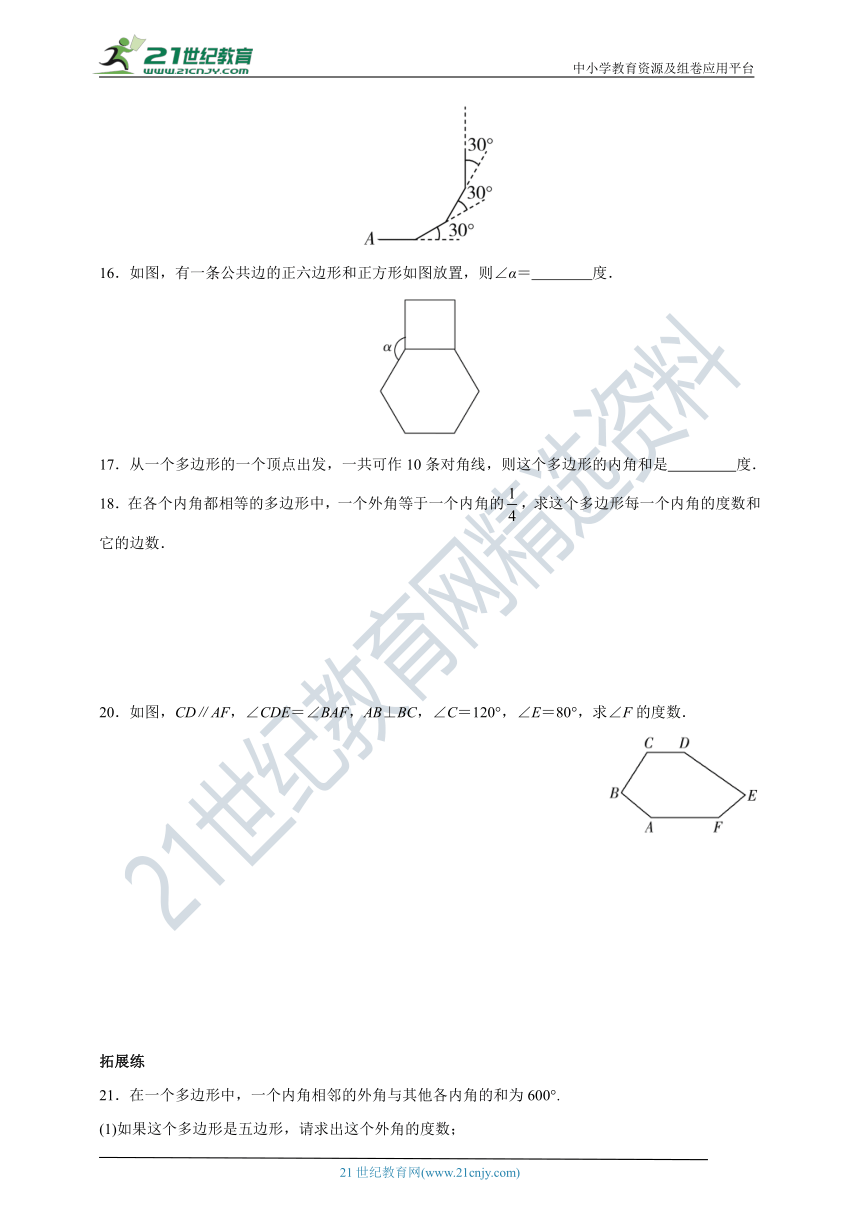
15.如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°……照这样走下去,他第一次回到出发地A点时,一共走了 米.
16.如图,有一条公共边的正六边形和正方形如图放置,则∠α= 度.
17.从一个多边形的一个顶点出发,一共可作10条对角线,则这个多边形的内角和是 度.
18.在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数.
20.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,求∠F的度数.
拓展练
21.在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.
(1)如果这个多边形是五边形,请求出这个外角的度数;
(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
参 考 答 案
1.C
2.C
3.D
4.180°
5.解:设原多边形的边数为n. 根据题意,得0°<(n-2)×180°-1125°<180°,解得8.25<n<9.25. ∵n为整数,∴n=9. ∴少加的这个内角为(9-2)×180°-1125°=135°. ∴原多边形的内角和为(9-2)×180°=1260°.
6.B
7.D
8.B
9.1260°
10.解:设这个多边形的边数为n,根据题意,得(n-2)×180°=3×360°-180°,解得n=7. 所以这个多边形的内角和为(7-2)×180°=900°.
11.A
12.D
13.D
14.C
15.180
16.150
17.1980
18.解:设该多边形为n边形.∵多边形一个外角等于一个内角的,∴多边形的内角和为360°×4=1440°,∴(n-2)×180°=1440°,解得n=10,∴该多边形每一个内角的度数为(360°÷10)×4=144°. 即该多边形每一个内角的度数为144°,该多边形的边数为10.
20.解:如图,连接AD. 在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°. ∵AB⊥BC,∴∠B=90°. 又∵∠C=120°,∴∠BAD+∠ADC=150°. ∵CD∥AF,∴∠ADC=∠DAF. 又∵∠CDE=∠BAF,∴∠EDA=∠BAD. ∴∠EDA+∠DAF=150°. 在四边形ADEF中,∠DAF+∠EDA+∠F+∠E=360°,∴∠F+∠E=360°-∠DAF-∠EDA=360°-150°=210°. 又∵∠E=80°,∴∠F=130°.
21.解:(1)设这个外角的度数是x°,根据题意,得(5-2)×180-(180-x)+x=600,解得x=120. 故这个外角的度数是120°.
(2)存在.设边数为n,这个外角的度数是y°,根据题意,得(n-2)×180-(180-y)+y=600,整理,得y=570-90n. ∵0<y<180,即0<570-90n<180,并且n为正整数,∴n=5或n=6. 将n=6代入(n-2)×180-(180-y)+y=600,解得y=30. 故此多边形的边数是6,外角的度数为30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级上册课堂同步练
第十一章 三角形
11.3 多边形及其内角和
11.3.2 多边形的内角和
分类练
知识点1 多边形的内角和
1.如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为( )
A.120° B.110° C.100° D.40°
2.若一个多边形的内角和为720°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
3.正十边形的每一个内角的度数为( )
A.120° B.135° C.140° D.144°
4.n边形的边每增加一条,它的内角和就增加 .
5.小辉同学在计算某个多边形的内角和时,求得的内角和为1125°,检查发现错误原因是少加了一个内角,求少加的这个内角是多少度?正确的结果应是多少?
知识点2 多边形的外角和
6.一个多边形的每一个外角都等于36°,则这个多边形的边数n等于( )
A.8 B.10 C.12 D.14
7.一个多边形的每个内角都等于135°,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
8.下列多边形中,内角和与外角和相等的是( )
A B C D
9.已知正多边形的一个外角等于40°,则这个正多边形的内角和的度数为 .
10.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数及内角和.
提升练
11.我们在探究“任意一个四边形内角和是多少度”时,采用的方法是连接四边形的一条对角线,把四边形分割成两个三角形,从而探究出任意四边形的内角和等于360°,这一过程体现的数学思想是( )
A.转化思想 B.方程思想 C.函数思想 D.数形结合思想
12.一个三角形,剪去一个角后所得的多边形内角和的度数是( )
A.180° B.360° C.540° D.180°或360°
13.将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.900°
14.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是 ( )
A.180° B.220° C.240° D.300°
15.如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°……照这样走下去,他第一次回到出发地A点时,一共走了 米.
16.如图,有一条公共边的正六边形和正方形如图放置,则∠α= 度.
17.从一个多边形的一个顶点出发,一共可作10条对角线,则这个多边形的内角和是 度.
18.在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数.
20.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,求∠F的度数.
拓展练
21.在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.
(1)如果这个多边形是五边形,请求出这个外角的度数;
(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
参 考 答 案
1.C
2.C
3.D
4.180°
5.解:设原多边形的边数为n. 根据题意,得0°<(n-2)×180°-1125°<180°,解得8.25<n<9.25. ∵n为整数,∴n=9. ∴少加的这个内角为(9-2)×180°-1125°=135°. ∴原多边形的内角和为(9-2)×180°=1260°.
6.B
7.D
8.B
9.1260°
10.解:设这个多边形的边数为n,根据题意,得(n-2)×180°=3×360°-180°,解得n=7. 所以这个多边形的内角和为(7-2)×180°=900°.
11.A
12.D
13.D
14.C
15.180
16.150
17.1980
18.解:设该多边形为n边形.∵多边形一个外角等于一个内角的,∴多边形的内角和为360°×4=1440°,∴(n-2)×180°=1440°,解得n=10,∴该多边形每一个内角的度数为(360°÷10)×4=144°. 即该多边形每一个内角的度数为144°,该多边形的边数为10.
20.解:如图,连接AD. 在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°. ∵AB⊥BC,∴∠B=90°. 又∵∠C=120°,∴∠BAD+∠ADC=150°. ∵CD∥AF,∴∠ADC=∠DAF. 又∵∠CDE=∠BAF,∴∠EDA=∠BAD. ∴∠EDA+∠DAF=150°. 在四边形ADEF中,∠DAF+∠EDA+∠F+∠E=360°,∴∠F+∠E=360°-∠DAF-∠EDA=360°-150°=210°. 又∵∠E=80°,∴∠F=130°.
21.解:(1)设这个外角的度数是x°,根据题意,得(5-2)×180-(180-x)+x=600,解得x=120. 故这个外角的度数是120°.
(2)存在.设边数为n,这个外角的度数是y°,根据题意,得(n-2)×180-(180-y)+y=600,整理,得y=570-90n. ∵0<y<180,即0<570-90n<180,并且n为正整数,∴n=5或n=6. 将n=6代入(n-2)×180-(180-y)+y=600,解得y=30. 故此多边形的边数是6,外角的度数为30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
