人教A版(2019)选择性必修第一册专题12:圆方程核心题型训练(Word版含答案)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册专题12:圆方程核心题型训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 321.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 03:05:23 | ||
图片预览




文档简介
《圆与方程》专题12-1 圆方程核心题型训练
(8套,10页,含答案)
使用说明: 有些同学学习后面《圆锥曲线》 、《导数》等章节时,发现《圆与方程》有缺漏,但又不想花太多时间系统学习,可以用这个专题训练一下,掌握好十种题型即可。
知识点:
圆的定义:
平面内到一定点的距离等于定长的点的集合叫圆,定点为圆心,定长为圆的半径。 2、圆的标准方程: 以点为圆心,为半径的圆的标准方程是. 特例:圆心在坐标原点,半径为的圆的方程是:. 3、点圆关系: 设点到圆心的距离为d,圆半径为r: (1)点在圆上 d=r; (2)点在圆外 d>r; (3)点在圆内 d<r. 3、点圆距离最值: (1)圆外一点,圆上一动点,讨论的最值
圆内一点,圆上一动点,讨论的最值
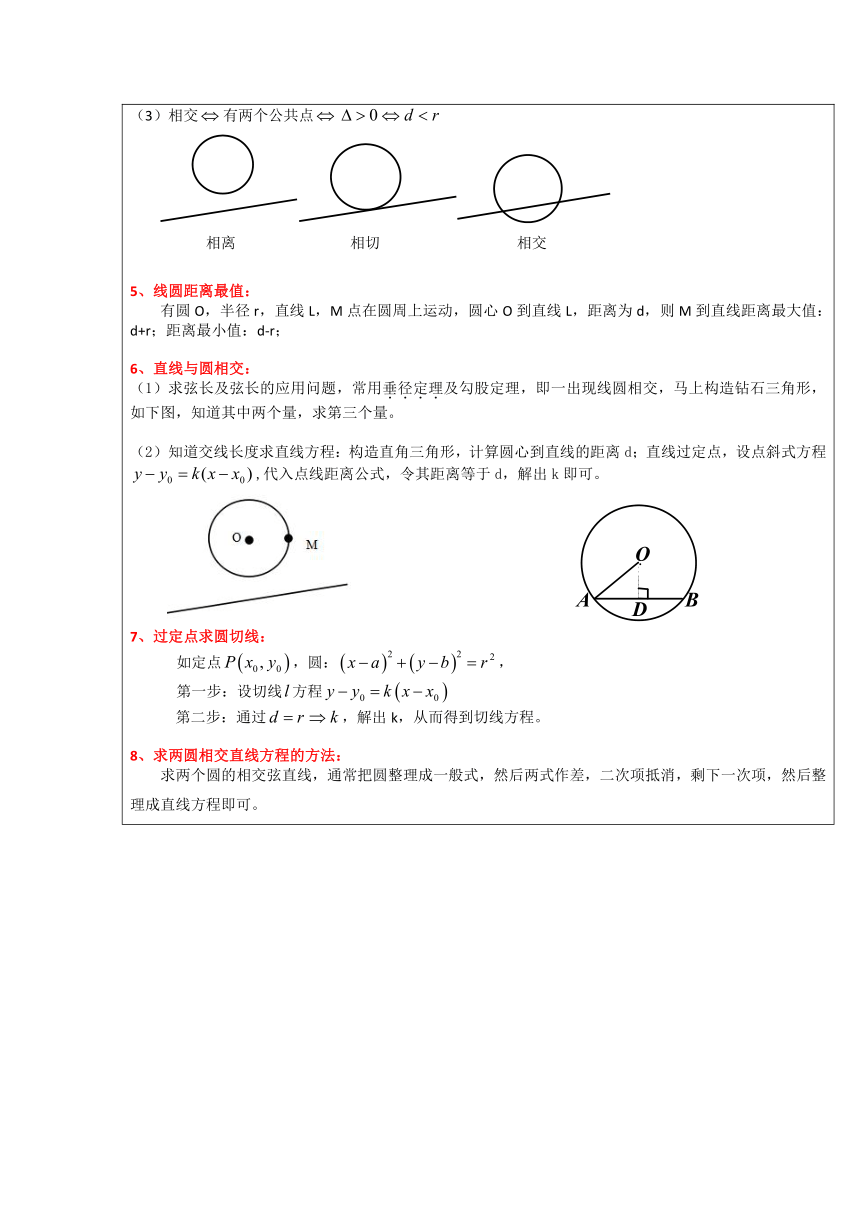
4、线圆关系: 直线与圆的位置关系有三种 (1)相离没有公共点 (2)相切只有一个公共点 (3)相交有两个公共点
相离 相切 相交 5、线圆距离最值: 有圆O,半径r,直线L,M点在圆周上运动,圆心O到直线L,距离为d,则M到直线距离最大值:d+r;距离最小值:d-r; 6、直线与圆相交: 求弦长及弦长的应用问题,常用垂径定理及勾股定理,即一出现线圆相交,马上构造钻石三角形,如下图,知道其中两个量,求第三个量。
知道交线长度求直线方程:构造直角三角形,计算圆心到直线的距离d;直线过定点,设点斜式方程,代入点线距离公式,令其距离等于d,解出k即可。 7、过定点求圆切线: 如定点,圆:, 第一步:设切线方程 第二步:通过,解出k,从而得到切线方程。 8、求两圆相交直线方程的方法: 求两个圆的相交弦直线,通常把圆整理成一般式,然后两式作差,二次项抵消,剩下一次项,然后整理成直线方程即可。
典型例题:
已知圆N的圆心为(-2,0),半径为1,求圆N方程;
(2)已知圆M的圆心在直线y=-x-3上,且过(1,-2),(-1,0),求圆M方程;
(3)已知圆M:,圆N:,点A(0,-2),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点A(0,-2),点B在圆M上运动,
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断直线L与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,直线L:,
求点B到直线直线L距离的最大值和最小值;
(7)已知圆M:,求直线y=2x-2与圆M相交弦长;
(8)已知圆M:,过点(0,3)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过原点的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:0]) [0: 答案:
(1); (2); (3)A在圆N外,A在圆M内;
(4)最小值1,最大值3; (5)与圆N相切,与圆M相交; (6)最小值0,最大值;
(7); (8)x=0或; (9); (10),;
]
专题12-1答案:(1);(2);(3)A在圆N外,A在圆M内;
(4)最小值1,最大值3; (5)与圆N相切,与圆M相交; (6)最小值0,最大值;
(7); (8)x=0或; (9); (10),;
《圆与方程》专题12-2 圆方程核心题型训练
已知圆M的圆心为(1,1),半径为1,求圆M方程;
(2)已知圆N的圆心在直线y=2x上,且过(-1,0),(0,-1),求圆N方程;
(3)已知圆M:,圆N:,点A(1,2),
判断点A与圆M、圆N的位置关系;
(4)已知圆N:,点A(1,2),点B在圆N上运动,求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:y=-2x+4,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点B在圆N上运动,直线L:y=-2x+4,
求点B到直线L距离的最大值和最小值;
(7)已知圆M:,求直线y=2x与圆M相交弦长;
(8)已知圆M:,过点(-1,-2)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过点(-1,-2)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:1]) [1: 答案:
(1); (2); (3)A在圆M上,A在圆N外;
(4)最小值,最大值; (5)与圆M相交,与圆N相离;
(6)最小值,最大值; (7); (8)或;
(9)或; (10),;
]
专题12-2答案: (1); (2); (3)A在圆M上,A在圆N外;
(4)最小值,最大值; (5)与圆M相交,与圆N相离;
(6)最小值,最大值; (7); (8)或;
(9)或; (10),;
《圆与方程》专题12-3 圆方程核心题型训练
(1)已知圆M的圆心为(2,-3),半径为3,求圆M方程;
(2)已知圆N的圆心在直线y=-3x上,且过(-5,0),(3,4),求圆N方程;
(3)已知圆M:,圆N:,点A(-3,4),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点A(-3,4),点B在圆M上运动,
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:y=x+1,
判断该直线与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,直线L:y=x+1,
求点B到直线L距离的最大值和最小值;
(7)已知圆N:,求直线y=-x+3与圆N相交弦长;
(8)已知圆N:,过点(5,5)的直线P被圆N截得的弦长为,求直线P的方程;
(9)已知圆M:,过点(-2,0)的直线Q与圆M相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程;([endnoteRef:2]) [2: 答案:
(1); (2); (3)A在圆N上,A在圆M外;
(4)最小值,最大值; (5)与圆M相离,与圆N相交;
(6)最小值,最大值; (7); (8)x-2y+5=0或2x-y-5=0;
(9)y=0或24x+7y+48=0; (10)4x-6y-29=0;
]
专题12-3答案: (1); (2);(3)A在圆N上,A在圆M外;
(4)最小值,最大值; (5)与圆M相离,与圆N相交;(6)最小值,最大值; (7); (8)x-2y+5=0或2x-y-5=0;(9)y=0或24x+7y+48=0; (10)4x-6y-29=0;
《圆与方程》专题12-4 圆方程核心题型训练
已知圆N的圆心为(1,0),半径为1,求圆N方程;
(2)已知圆M的圆心在直线y=x+1上,且过(1,4),(-1,2),求圆M方程;
(3)已知圆M:,圆N:,点A(-1,2),
判断点A与圆M、圆N的位置关系;
(4)已知圆N:,点B在圆N上运动,点A(-1,2),
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:y=0,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点B在圆N上运动,求点B到直线y=2x+2距离的最大值和最小值;
(7)已知圆M:,求直线y=2x+1与圆M相交弦长;
(8)已知圆N:,过原点的直线P被圆N截得的弦长为,求直线P的方程;
(9)已知圆N:,过点(2,2)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:3]) [3: 答案:
(1); (2); (3)A在圆N外,A在圆M上;
(4)最小值,最大值; (5)与圆M相切,与圆N相交;
(6)最小值,最大值; (7); (8);
(9)或; (10),;
]
专题12-4答案: (1);(2);(3)A在圆N外,A在圆M上;
(4)min=,max=;(5)与圆M相切,与圆N相交;(6)min=,max=; (7); (8); (9)或; (10),;
《圆与方程》专题12-5 圆方程核心题型训练
(1)已知圆N的圆心为(1,-2),半径为,求圆N方程;
(2)已知圆M的圆心在直线y=-4x上,且过(0,3),(1,),求圆M方程;
(3)已知圆M:,圆N:,点A(3,-3),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点B在圆M上运动,点A(3,-3),求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点E在圆N上运动,直线L:,
求点E到直线L距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆N:,过点(2,1)的直线P被圆N截得的弦长为4,求直线P的方程;
(9)已知圆M:,过点(1,3)的直线Q与圆M相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:4]) [4: 答案:
(1); (2); (3)A在圆N上,A在圆M外;
(4)最小值,最大值; (5)与圆M相交,与圆N相离;
(6)最小值,最大值; (7); (8)x=2或4x-3y-5=0;
(9)或; (10),;
]
专题12-5答案:(1); (2);(3)A在圆N上,A在圆M外;
(4)最小值,最大值;(5)与M相交,与N相离;(6)小,大; (7); (8)x=2或4x-3y-5=0;(9)或; (10),;
《圆与方程》专题12-6 圆方程核心题型训练
(1)已知圆N的圆心为(2,1),半径为1,求圆N方程;
(2)已知圆M的圆心在直线y=3x-8上,且过(1,-1),(3,-1),求圆M方程;
(3)已知圆M:,圆N:,点A(3,-2),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点B在圆M上运动,点A(3,-2),
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,直线L:,
求点B到直线直线L距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆M:,过点(3,0)的直线P被圆M截得的弦长为2,求直线P的方程;
(9)已知圆N:,过原点的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:5]) [5: 答案:
(1); (2); (3)A在圆N外,A在圆M内;
(4)最小值,最大值; (5)与圆N相交,与圆M相离;
(6),; (7); (8)x=3或;
(9)或; (10),;
]
专题12-6答案:(1);(2);(3)A在圆N外,A在圆M内;(4)最小值,最大值; (5)与圆N相交,与圆M相离;(6),; (7); (8)x=3或; (9)或; (10),;
《圆与方程》专题12-7 圆方程核心题型训练
(1)已知圆N的圆心为(0,0),半径为2,求圆N方程;
(2)已知圆M的圆心在直线y=-2x+1上,且过(-1,-3),(2,0),求圆M方程;
(3)已知圆M:,圆N:,点A(1,1),
判断点A与圆M、圆N的位置关系;
(4)已知圆N:,点B在圆N上运动,点A(1,1),求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点B在圆N上运动,求点B到直线距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆M:,过点(-1,0)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过点(2,4)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:6]) [6: 答案:
(1); (2); (3)A在圆N内,A在圆M外;
(4)最小值,最大值; (5)与圆N相交,与圆M相离;
(6)最小值,最大值; (7)4; (8)或;
(9)或; (10),;
]
专题12-7答案:(1); (2); (3)A在圆N内,A在圆M外;
(4)最小值,最大值; (5)与圆N相交,与圆M相离;(6)最小值,最大值; (7)4;(8)或;(9)或;(10),;
《圆与方程》专题12-8 圆方程核心题型训练
(1)已知圆M的圆心为(3,-1),半径为3,求圆M方程;
(2)已知圆N的圆心在直线y=3x-3上,且过(0,3),(2,1),求圆N方程;
(3)已知圆M:,圆N:,点A(4,3),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点B在圆M上运动,点A(4,3),
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,
求点B到直线距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆M:,过点(0,-1)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过点(0,-1)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:7]) [7: 答案:
(1); (2); (3)A在圆M外,A在圆N上;
(4)最小值,最大值; (5)与圆N相交,与圆M相交;
(6)最小值,最大值; (7)4; (8)或;
(9)x=0或; (10),;
]
专题12-8答案:(1);(2);(3)A在圆M外,A在圆N上;(4)最小值,最大值;(5)与圆N相交,与圆M相交;(6)最小,最大; (7)4;(8)或;(9)x=0或;(10),;
(8套,10页,含答案)
使用说明: 有些同学学习后面《圆锥曲线》 、《导数》等章节时,发现《圆与方程》有缺漏,但又不想花太多时间系统学习,可以用这个专题训练一下,掌握好十种题型即可。
知识点:
圆的定义:
平面内到一定点的距离等于定长的点的集合叫圆,定点为圆心,定长为圆的半径。 2、圆的标准方程: 以点为圆心,为半径的圆的标准方程是. 特例:圆心在坐标原点,半径为的圆的方程是:. 3、点圆关系: 设点到圆心的距离为d,圆半径为r: (1)点在圆上 d=r; (2)点在圆外 d>r; (3)点在圆内 d<r. 3、点圆距离最值: (1)圆外一点,圆上一动点,讨论的最值
圆内一点,圆上一动点,讨论的最值
4、线圆关系: 直线与圆的位置关系有三种 (1)相离没有公共点 (2)相切只有一个公共点 (3)相交有两个公共点
相离 相切 相交 5、线圆距离最值: 有圆O,半径r,直线L,M点在圆周上运动,圆心O到直线L,距离为d,则M到直线距离最大值:d+r;距离最小值:d-r; 6、直线与圆相交: 求弦长及弦长的应用问题,常用垂径定理及勾股定理,即一出现线圆相交,马上构造钻石三角形,如下图,知道其中两个量,求第三个量。
知道交线长度求直线方程:构造直角三角形,计算圆心到直线的距离d;直线过定点,设点斜式方程,代入点线距离公式,令其距离等于d,解出k即可。 7、过定点求圆切线: 如定点,圆:, 第一步:设切线方程 第二步:通过,解出k,从而得到切线方程。 8、求两圆相交直线方程的方法: 求两个圆的相交弦直线,通常把圆整理成一般式,然后两式作差,二次项抵消,剩下一次项,然后整理成直线方程即可。
典型例题:
已知圆N的圆心为(-2,0),半径为1,求圆N方程;
(2)已知圆M的圆心在直线y=-x-3上,且过(1,-2),(-1,0),求圆M方程;
(3)已知圆M:,圆N:,点A(0,-2),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点A(0,-2),点B在圆M上运动,
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断直线L与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,直线L:,
求点B到直线直线L距离的最大值和最小值;
(7)已知圆M:,求直线y=2x-2与圆M相交弦长;
(8)已知圆M:,过点(0,3)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过原点的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:0]) [0: 答案:
(1); (2); (3)A在圆N外,A在圆M内;
(4)最小值1,最大值3; (5)与圆N相切,与圆M相交; (6)最小值0,最大值;
(7); (8)x=0或; (9); (10),;
]
专题12-1答案:(1);(2);(3)A在圆N外,A在圆M内;
(4)最小值1,最大值3; (5)与圆N相切,与圆M相交; (6)最小值0,最大值;
(7); (8)x=0或; (9); (10),;
《圆与方程》专题12-2 圆方程核心题型训练
已知圆M的圆心为(1,1),半径为1,求圆M方程;
(2)已知圆N的圆心在直线y=2x上,且过(-1,0),(0,-1),求圆N方程;
(3)已知圆M:,圆N:,点A(1,2),
判断点A与圆M、圆N的位置关系;
(4)已知圆N:,点A(1,2),点B在圆N上运动,求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:y=-2x+4,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点B在圆N上运动,直线L:y=-2x+4,
求点B到直线L距离的最大值和最小值;
(7)已知圆M:,求直线y=2x与圆M相交弦长;
(8)已知圆M:,过点(-1,-2)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过点(-1,-2)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:1]) [1: 答案:
(1); (2); (3)A在圆M上,A在圆N外;
(4)最小值,最大值; (5)与圆M相交,与圆N相离;
(6)最小值,最大值; (7); (8)或;
(9)或; (10),;
]
专题12-2答案: (1); (2); (3)A在圆M上,A在圆N外;
(4)最小值,最大值; (5)与圆M相交,与圆N相离;
(6)最小值,最大值; (7); (8)或;
(9)或; (10),;
《圆与方程》专题12-3 圆方程核心题型训练
(1)已知圆M的圆心为(2,-3),半径为3,求圆M方程;
(2)已知圆N的圆心在直线y=-3x上,且过(-5,0),(3,4),求圆N方程;
(3)已知圆M:,圆N:,点A(-3,4),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点A(-3,4),点B在圆M上运动,
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:y=x+1,
判断该直线与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,直线L:y=x+1,
求点B到直线L距离的最大值和最小值;
(7)已知圆N:,求直线y=-x+3与圆N相交弦长;
(8)已知圆N:,过点(5,5)的直线P被圆N截得的弦长为,求直线P的方程;
(9)已知圆M:,过点(-2,0)的直线Q与圆M相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程;([endnoteRef:2]) [2: 答案:
(1); (2); (3)A在圆N上,A在圆M外;
(4)最小值,最大值; (5)与圆M相离,与圆N相交;
(6)最小值,最大值; (7); (8)x-2y+5=0或2x-y-5=0;
(9)y=0或24x+7y+48=0; (10)4x-6y-29=0;
]
专题12-3答案: (1); (2);(3)A在圆N上,A在圆M外;
(4)最小值,最大值; (5)与圆M相离,与圆N相交;(6)最小值,最大值; (7); (8)x-2y+5=0或2x-y-5=0;(9)y=0或24x+7y+48=0; (10)4x-6y-29=0;
《圆与方程》专题12-4 圆方程核心题型训练
已知圆N的圆心为(1,0),半径为1,求圆N方程;
(2)已知圆M的圆心在直线y=x+1上,且过(1,4),(-1,2),求圆M方程;
(3)已知圆M:,圆N:,点A(-1,2),
判断点A与圆M、圆N的位置关系;
(4)已知圆N:,点B在圆N上运动,点A(-1,2),
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:y=0,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点B在圆N上运动,求点B到直线y=2x+2距离的最大值和最小值;
(7)已知圆M:,求直线y=2x+1与圆M相交弦长;
(8)已知圆N:,过原点的直线P被圆N截得的弦长为,求直线P的方程;
(9)已知圆N:,过点(2,2)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:3]) [3: 答案:
(1); (2); (3)A在圆N外,A在圆M上;
(4)最小值,最大值; (5)与圆M相切,与圆N相交;
(6)最小值,最大值; (7); (8);
(9)或; (10),;
]
专题12-4答案: (1);(2);(3)A在圆N外,A在圆M上;
(4)min=,max=;(5)与圆M相切,与圆N相交;(6)min=,max=; (7); (8); (9)或; (10),;
《圆与方程》专题12-5 圆方程核心题型训练
(1)已知圆N的圆心为(1,-2),半径为,求圆N方程;
(2)已知圆M的圆心在直线y=-4x上,且过(0,3),(1,),求圆M方程;
(3)已知圆M:,圆N:,点A(3,-3),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点B在圆M上运动,点A(3,-3),求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点E在圆N上运动,直线L:,
求点E到直线L距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆N:,过点(2,1)的直线P被圆N截得的弦长为4,求直线P的方程;
(9)已知圆M:,过点(1,3)的直线Q与圆M相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:4]) [4: 答案:
(1); (2); (3)A在圆N上,A在圆M外;
(4)最小值,最大值; (5)与圆M相交,与圆N相离;
(6)最小值,最大值; (7); (8)x=2或4x-3y-5=0;
(9)或; (10),;
]
专题12-5答案:(1); (2);(3)A在圆N上,A在圆M外;
(4)最小值,最大值;(5)与M相交,与N相离;(6)小,大; (7); (8)x=2或4x-3y-5=0;(9)或; (10),;
《圆与方程》专题12-6 圆方程核心题型训练
(1)已知圆N的圆心为(2,1),半径为1,求圆N方程;
(2)已知圆M的圆心在直线y=3x-8上,且过(1,-1),(3,-1),求圆M方程;
(3)已知圆M:,圆N:,点A(3,-2),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点B在圆M上运动,点A(3,-2),
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,直线L:,
求点B到直线直线L距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆M:,过点(3,0)的直线P被圆M截得的弦长为2,求直线P的方程;
(9)已知圆N:,过原点的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:5]) [5: 答案:
(1); (2); (3)A在圆N外,A在圆M内;
(4)最小值,最大值; (5)与圆N相交,与圆M相离;
(6),; (7); (8)x=3或;
(9)或; (10),;
]
专题12-6答案:(1);(2);(3)A在圆N外,A在圆M内;(4)最小值,最大值; (5)与圆N相交,与圆M相离;(6),; (7); (8)x=3或; (9)或; (10),;
《圆与方程》专题12-7 圆方程核心题型训练
(1)已知圆N的圆心为(0,0),半径为2,求圆N方程;
(2)已知圆M的圆心在直线y=-2x+1上,且过(-1,-3),(2,0),求圆M方程;
(3)已知圆M:,圆N:,点A(1,1),
判断点A与圆M、圆N的位置关系;
(4)已知圆N:,点B在圆N上运动,点A(1,1),求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆N:,点B在圆N上运动,求点B到直线距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆M:,过点(-1,0)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过点(2,4)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:6]) [6: 答案:
(1); (2); (3)A在圆N内,A在圆M外;
(4)最小值,最大值; (5)与圆N相交,与圆M相离;
(6)最小值,最大值; (7)4; (8)或;
(9)或; (10),;
]
专题12-7答案:(1); (2); (3)A在圆N内,A在圆M外;
(4)最小值,最大值; (5)与圆N相交,与圆M相离;(6)最小值,最大值; (7)4;(8)或;(9)或;(10),;
《圆与方程》专题12-8 圆方程核心题型训练
(1)已知圆M的圆心为(3,-1),半径为3,求圆M方程;
(2)已知圆N的圆心在直线y=3x-3上,且过(0,3),(2,1),求圆N方程;
(3)已知圆M:,圆N:,点A(4,3),
判断点A与圆M、圆N的位置关系;
(4)已知圆M:,点B在圆M上运动,点A(4,3),
求A、B距离的最大值和最小值;
(5)已知圆M:,圆N:,直线L:,
判断该直线与圆M、圆N的位置关系;
(6)已知圆M:,点B在圆M上运动,
求点B到直线距离的最大值和最小值;
(7)已知圆M:,求直线与圆M相交弦长;
(8)已知圆M:,过点(0,-1)的直线P被圆M截得的弦长为,
求直线P的方程;
(9)已知圆N:,过点(0,-1)的直线Q与圆N相切,求直线Q的方程;
(10)已知圆M:,圆N:,圆M、圆N相交于C、D两点,
求直线CD的方程,以及长度;([endnoteRef:7]) [7: 答案:
(1); (2); (3)A在圆M外,A在圆N上;
(4)最小值,最大值; (5)与圆N相交,与圆M相交;
(6)最小值,最大值; (7)4; (8)或;
(9)x=0或; (10),;
]
专题12-8答案:(1);(2);(3)A在圆M外,A在圆N上;(4)最小值,最大值;(5)与圆N相交,与圆M相交;(6)最小,最大; (7)4;(8)或;(9)x=0或;(10),;
