人教版 七年级上册 3.3 解一元一次方程(二)——去括号与去分母 学案(无答案)
文档属性
| 名称 | 人教版 七年级上册 3.3 解一元一次方程(二)——去括号与去分母 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览


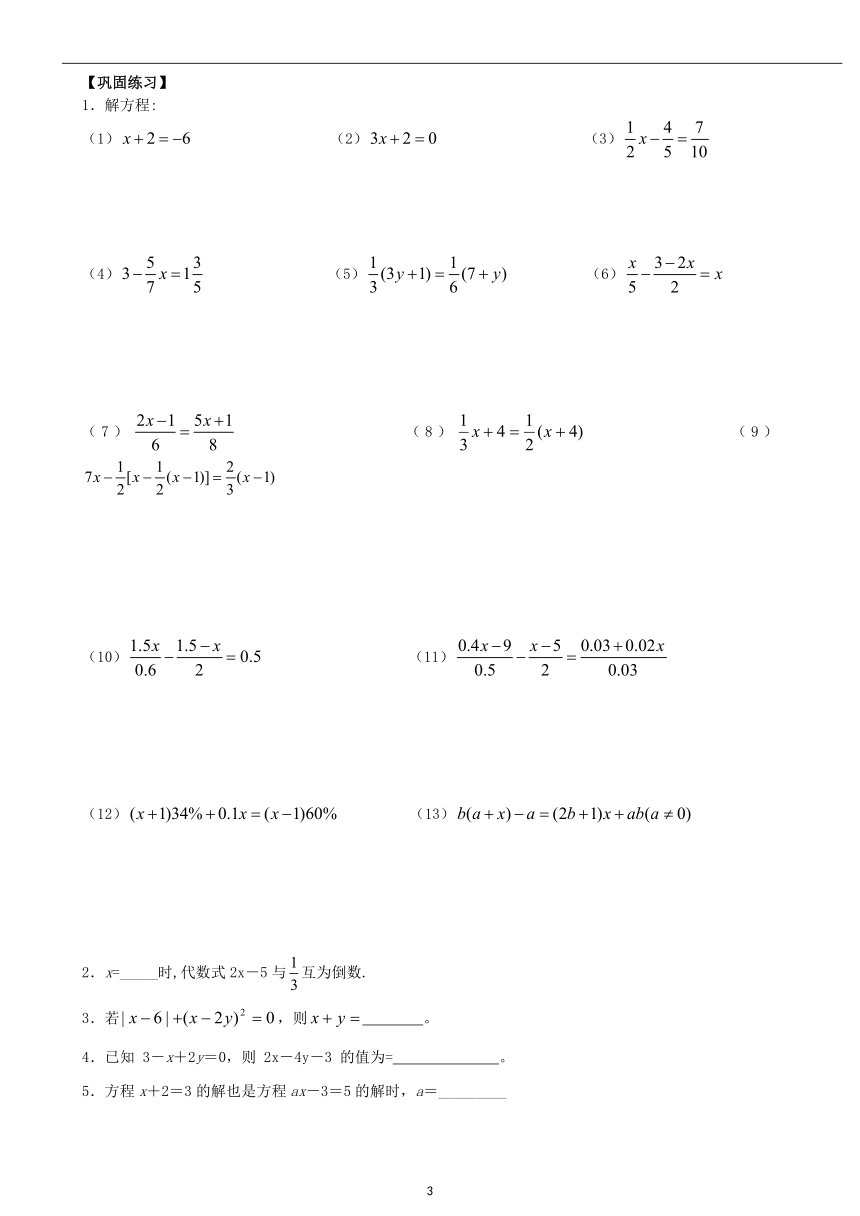
文档简介
一元一次方程
【知识点一:一元一次方程概念】
(1)用等号“=”来表示相等关系的式子,叫做等式。
(2)含有未知数的等式叫做方程。
(3)只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程.
【典型例题】
1.判断下列各式是不是方程:
(1)-7x+3 (2)1+4=5 (3) (4)
(5) (6) (7)8x-4 (8)4b=4b
2.判断下列方程中是不是一元一次方程:
① ②0.1x=1 ③
④ ⑤x=-2 ⑥x-2y=0 ⑦
【巩固练习】
1.下列各式中,不是等式的式子是( )
A.3+2=6; B.; C.; D.
2.下列说法中,正确的是( )
A.方程是等式; B.等式是方程; C.含有字母的等式是方程; D.不含字母的方程是等式
3.下列四个式子中,是方程的是( )
A.1 + 2 + 3 + 4 = 10 B.2x-3 C.x = 1 D.|10. 5|= 0. 5
4.若方程 是关于X的一元一次方程,则k=
【知识点二:解一元一次方程】
(1)使方程左右两边值相等的未知数的值,叫做方程的解;求方程解的过程,叫做解方程。
(2)解一元一次方程的一般步骤: 去分母→去括号→移项→合并同类项→系数化1
例:.
解:第一次去分母,得
第一次去括号,得
,
第二次去分母,得
移项,合并同类项,得
把系数化为1,得
.
【典型例题】
例1.利用等式的性质解方程:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;等式两边都乘以(或除以)同一个数(除数不为0),所得结果仍是等式。
(1) (2) (3)
例2.(1) (2) (3)
例3.(1) (2);
例4.(1) (2)
例5.(1) (2)
【巩固练习】
1.解方程:
(1) (2) (3)
(4) (5) (6)
(7) (8) (9)
(10) (11)
(12) (13)
2.x=_____时,代数式2x-5与互为倒数.
3.若,则 。
4.已知 3-x+2y=0,则 2x-4y-3 的值为= 。
5.方程x+2=3的解也是方程ax-3=5的解时,a=_________
6.方程(x-3)(2x+5)=0的解是 ( )
A.x=3; B.x=0; C.x=-或x=3; D.以上都不对
7.已知x=1是方程2x-2=x-m的解,则关于y的方程m(y+4)=2my+4m的解是( )
A.y=1 B.y=-1 C.y=0 D.无法确定
8.若关于x的方程kx-2x=14的解是正整数,则k的值有( )个
A.1个 B.2个 C.3个 D.4个
9.方程3x-5y=17,用含x的代数式表示y,则y=_______,当x=-1时,y=______.
10.已知关于的方程的解是,则的值是多少?
11.已知是方程的根,求代数式的值.
【提高训练】
一、解方程:主要是复杂的一元一次方程及含参数的方程
1、解下列方程:
⑴ ⑵
⑶ ⑷
⑸ ⑹
⑺ ⑻
2、解下列关于x 的方程:
⑴ ⑵
⑶ ⑷
⑸ ⑹
3、是方程 的解,又是方程 的解,求 b
4、小张在解方程(x为未知数)时,误将 - 2x 看成 2x 得到的解为 ,
请你求出原来方程的解
二、关于一元一次方程解的情况
一元一次方程 的解由的取值来确定:
若,则方程有唯一解;
若,且,方程变为,则方程有无穷多个解
若,且,方程变为,则方程无解
1、已知关于x 的方程 无解,求 a
2、已知关于x 的方程 有唯一的解,求这个方程的解
3、已知关于x 的方程 无穷多解,求 a 、b
4、不论 k为何值时,总是关于x 的方程 的解,求a 、b
5、关于x 的方程 的解为整数,求正整数k
6、关于 x的方程 的解为整数,求整数k
7、关于x 的方程 有一个正整数解,求最小正整数a
8、已知:关于x 的方程 仅有正整数解,并且和关于x 的方程 是同解方程,若 ,求这个方程的解。
1
【知识点一:一元一次方程概念】
(1)用等号“=”来表示相等关系的式子,叫做等式。
(2)含有未知数的等式叫做方程。
(3)只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程.
【典型例题】
1.判断下列各式是不是方程:
(1)-7x+3 (2)1+4=5 (3) (4)
(5) (6) (7)8x-4 (8)4b=4b
2.判断下列方程中是不是一元一次方程:
① ②0.1x=1 ③
④ ⑤x=-2 ⑥x-2y=0 ⑦
【巩固练习】
1.下列各式中,不是等式的式子是( )
A.3+2=6; B.; C.; D.
2.下列说法中,正确的是( )
A.方程是等式; B.等式是方程; C.含有字母的等式是方程; D.不含字母的方程是等式
3.下列四个式子中,是方程的是( )
A.1 + 2 + 3 + 4 = 10 B.2x-3 C.x = 1 D.|10. 5|= 0. 5
4.若方程 是关于X的一元一次方程,则k=
【知识点二:解一元一次方程】
(1)使方程左右两边值相等的未知数的值,叫做方程的解;求方程解的过程,叫做解方程。
(2)解一元一次方程的一般步骤: 去分母→去括号→移项→合并同类项→系数化1
例:.
解:第一次去分母,得
第一次去括号,得
,
第二次去分母,得
移项,合并同类项,得
把系数化为1,得
.
【典型例题】
例1.利用等式的性质解方程:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;等式两边都乘以(或除以)同一个数(除数不为0),所得结果仍是等式。
(1) (2) (3)
例2.(1) (2) (3)
例3.(1) (2);
例4.(1) (2)
例5.(1) (2)
【巩固练习】
1.解方程:
(1) (2) (3)
(4) (5) (6)
(7) (8) (9)
(10) (11)
(12) (13)
2.x=_____时,代数式2x-5与互为倒数.
3.若,则 。
4.已知 3-x+2y=0,则 2x-4y-3 的值为= 。
5.方程x+2=3的解也是方程ax-3=5的解时,a=_________
6.方程(x-3)(2x+5)=0的解是 ( )
A.x=3; B.x=0; C.x=-或x=3; D.以上都不对
7.已知x=1是方程2x-2=x-m的解,则关于y的方程m(y+4)=2my+4m的解是( )
A.y=1 B.y=-1 C.y=0 D.无法确定
8.若关于x的方程kx-2x=14的解是正整数,则k的值有( )个
A.1个 B.2个 C.3个 D.4个
9.方程3x-5y=17,用含x的代数式表示y,则y=_______,当x=-1时,y=______.
10.已知关于的方程的解是,则的值是多少?
11.已知是方程的根,求代数式的值.
【提高训练】
一、解方程:主要是复杂的一元一次方程及含参数的方程
1、解下列方程:
⑴ ⑵
⑶ ⑷
⑸ ⑹
⑺ ⑻
2、解下列关于x 的方程:
⑴ ⑵
⑶ ⑷
⑸ ⑹
3、是方程 的解,又是方程 的解,求 b
4、小张在解方程(x为未知数)时,误将 - 2x 看成 2x 得到的解为 ,
请你求出原来方程的解
二、关于一元一次方程解的情况
一元一次方程 的解由的取值来确定:
若,则方程有唯一解;
若,且,方程变为,则方程有无穷多个解
若,且,方程变为,则方程无解
1、已知关于x 的方程 无解,求 a
2、已知关于x 的方程 有唯一的解,求这个方程的解
3、已知关于x 的方程 无穷多解,求 a 、b
4、不论 k为何值时,总是关于x 的方程 的解,求a 、b
5、关于x 的方程 的解为整数,求正整数k
6、关于 x的方程 的解为整数,求整数k
7、关于x 的方程 有一个正整数解,求最小正整数a
8、已知:关于x 的方程 仅有正整数解,并且和关于x 的方程 是同解方程,若 ,求这个方程的解。
1
