北师大版物理八年级下册课课练:专题训练 压强和浮力的综合应用(含答案)
文档属性
| 名称 | 北师大版物理八年级下册课课练:专题训练 压强和浮力的综合应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-23 19:02:47 | ||
图片预览


文档简介
专题训练 [压强和浮力的综合应用]
基础题
1.(2021贵港)2020年11月28日上午8时30分左右,随着一阵汽笛声,在马里亚纳海沟结束科考任务的“探索一号”科考船搭载成功实现10909 m坐底纪录的“奋斗者号”胜利返航。已知海水的密度为1.03×103 kg/m3,关于“奋斗者号”在海面下下潜的过程,下列说法正确的是 ( )
A.“奋斗者号”受到海水的压强不变,受到海水的浮力不变
B.“奋斗者号”受到海水的压强变大,受到海水的浮力不变
C.“奋斗者号”受到海水的压强变大,受到海水的浮力变大
D.“奋斗者号”受到海水的压强变小,受到海水的浮力变小
2.(2021昆明)一个气球下挂一铁块置于水中某一位置静止(如图图所示)。现用手轻轻向下推一下气球,那么手离开气球后,气球和铁块的运动情况是 ( )
A.加速向下运动 B.匀速向下运动
C.减速向下运动 D.仍然处于静止状态
3.用相同木材做成的两个质量相等的长方体木块A和B,A的底面积大于B的底面积,把它们分别放入水中和酒精中,静止时如图图所示,则下列关于木块底部受到液体的压力和压强的大小关系,判断正确的是 ( )
A.FA>FB,pAC.FA=FB,pA>pB D.FA=FB,pA4.如图图(a)所示是A、B两种液体内部的压强与深度的关系图像,设A液体的密度为ρA,B液体的密度为ρB,把同一木块分别放入盛有A、B两种液体的容器中,如图图图(b)所示,则下列说法正确的是 ( )
A.乙容器中木块排开的液体所受的重力大
B.木块在甲容器中时受到的浮力大
C.木块底部在乙容器中时受到的压强大
D.甲容器中盛的是A液体
5.如图图所示,“A”和“B”表示满载的轮船在海水或江水中静止时液面的位置。图中的轮船在 (选填“江水”或“海水”)中停泊。轮船满载时排开海水的质量为6000 t,则它在海水中满载时受到的浮力是 N;轮船在江水中,船底所受水的压强是6×104 Pa,船底浸入水中的深度是 。(g取10 N/kg,ρ江水=1.0×103 kg/m3,ρ海水=1.03×103 kg/m3)
能力题
6.如图图所示,将三个完全相同的鸡蛋分别放入盛有不同液体的烧杯中,鸡蛋在甲杯中沉底,在乙杯中悬浮,在丙杯中漂浮,且各杯中液体的深度相同。则下列判断中正确的是 ( )
A.三种液体的密度关系为ρ甲=ρ乙>ρ丙
B.鸡蛋排开三种液体的质量关系为m甲=m乙>m丙
C.鸡蛋受到三种液体的浮力关系为F甲D.三种液体对容器底部的压强关系为p甲=p乙>p丙
7.(2021临沂)放在水平桌面上的甲、乙两个相同的容器中盛有同种液体,体积相等的a、b两个物体在液体中静止时,两液面相平,如图图所示。则 ( )
A.物体a的密度大
B.物体b受到的浮力小
C.甲容器底部受到的压力小
D.两容器对桌面的压强一样大
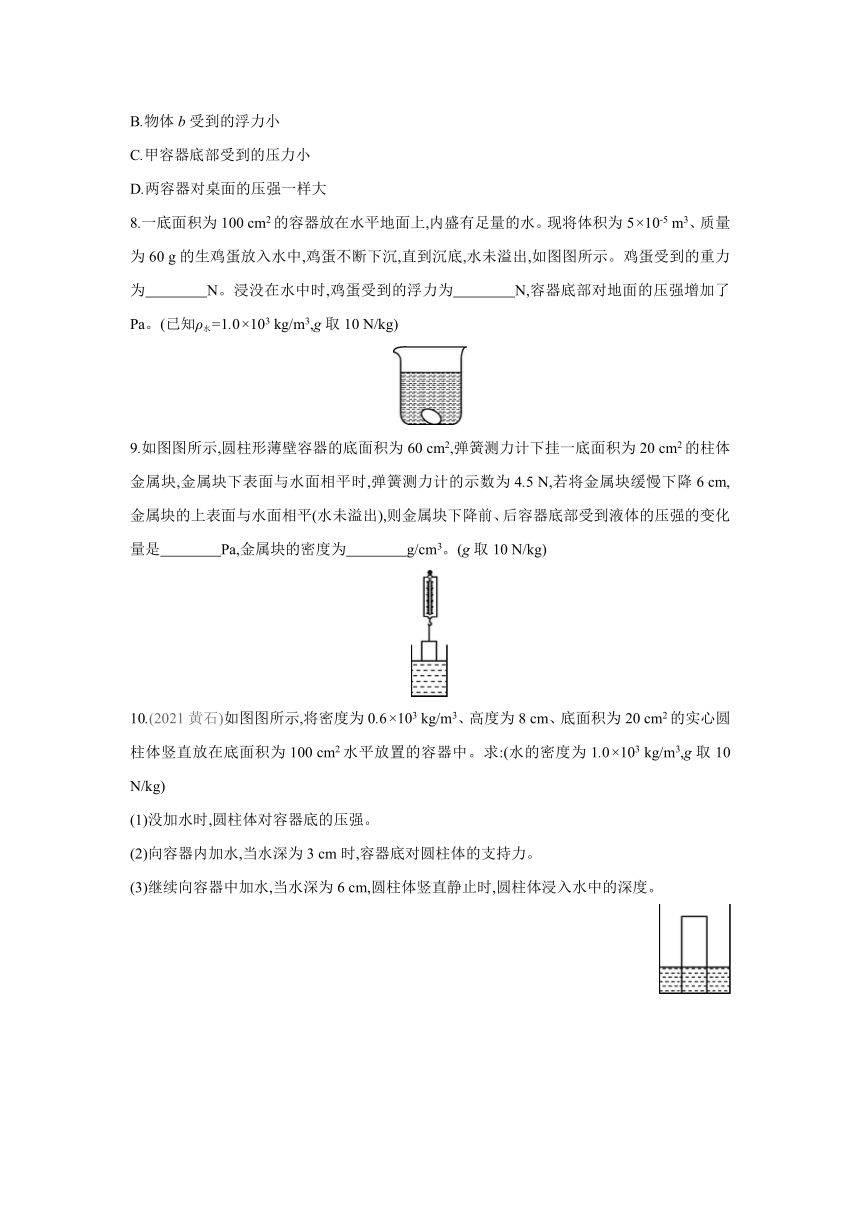
8.一底面积为100 cm2的容器放在水平地面上,内盛有足量的水。现将体积为5×10-5 m3、质量为60 g的生鸡蛋放入水中,鸡蛋不断下沉,直到沉底,水未溢出,如图图所示。鸡蛋受到的重力为 N。浸没在水中时,鸡蛋受到的浮力为 N,容器底部对地面的压强增加了 Pa。(已知ρ水=1.0×103 kg/m3,g取10 N/kg)
9.如图图所示,圆柱形薄壁容器的底面积为60 cm2,弹簧测力计下挂一底面积为20 cm2的柱体金属块,金属块下表面与水面相平时,弹簧测力计的示数为4.5 N,若将金属块缓慢下降6 cm,金属块的上表面与水面相平(水未溢出),则金属块下降前、后容器底部受到液体的压强的变化量是 Pa,金属块的密度为 g/cm3。(g取10 N/kg)
10.(2021黄石)如图图所示,将密度为0.6×103 kg/m3、高度为8 cm、底面积为20 cm2的实心圆柱体竖直放在底面积为100 cm2水平放置的容器中。求:(水的密度为1.0×103 kg/m3,g取10 N/kg)
(1)没加水时,圆柱体对容器底的压强。
(2)向容器内加水,当水深为3 cm时,容器底对圆柱体的支持力。
(3)继续向容器中加水,当水深为6 cm,圆柱体竖直静止时,圆柱体浸入水中的深度。
答案
压强和浮力的综合应用
1.B “奋斗者号”下潜的过程中,所处深度h增大,海水的密度不变,由p=ρgh可知,它受到的压强变大,“奋斗者号”没入海水中后,下潜的过程中,排开海水的体积V排不变,由于海水的密度不变,则根据F浮=ρ液gV排可知,受到的浮力不变,故B正确。
2.A 由图可知,气球和铁块处于静止状态,受到的浮力等于总的重力,现用手轻轻向下推一下气球,气球所处深度增加,压强增大,气球体积减小,排开液体的体积减小,浮力减小,且小于重力,那么手离开气球后,气球和铁块会加速向下运动,故A正确。
3.D A和B的质量相同,根据G=mg可知,它们的重力相同;A和B在液体中都处于漂浮状态,故所受浮力和重力大小相等,都为F浮=G;浮力产生的原因为上、下表面的压力差,A、B上表面不受液体压力,故A、B下表面所受的液体压力都等于所受浮力的大小,即FA=FB=
F浮;A的底面积大于B的底面积,根据p=可知,木块底部受到液体的压强pA4.D 由图可知,同一木块在A、B两种液体中都处于漂浮状态,根据物体的浮沉条件可知,F浮甲=F浮乙=G,即浮力相等,则排开的液体重力相同,故A、B错误;根据浮力产生的原因可知,木块在两种液体中,其下表面受到的压力相同,底面积相同,根据p=可知,受到的压强相同,故C错误;由图可知,<,且同一木块受到的浮力不变,根据F浮=ρ液gV排可知,ρA>ρB,所以甲容器中盛的是密度较大的A液体,故D正确。
5.海水 6×107 6 m
在海水和江水中,轮船都漂浮,浮力和自身的重力大小相等,即浮力大小不变;因海水的密度大于江水的密度,则根据公式F浮=ρ液gV排可知,轮船排开海水的体积小于排开江水的体积,即轮船在海水中的吃水线高度较低,所以图中的轮船是在海水中停泊的;根据阿基米德原理得,轮船所受的浮力:F浮=G排=m排g=6000×103 kg×10 N/kg=6×107 N;由液体压强公式p=ρgh得,船底浸入江水中的深度:h===6 m。
6.C 鸡蛋在甲杯中沉底,甲杯液体的密度小于鸡蛋的密度;在乙杯中悬浮,乙杯液体的密度等于鸡蛋的密度;在丙杯中漂浮,丙杯液体的密度大于鸡蛋的密度,三种液体的密度关系为ρ甲<ρ乙<ρ丙,故A错误。鸡蛋在甲杯中沉底,浮力小于鸡蛋的重力,则排开液体的质量小于鸡蛋的质量;在乙杯中悬浮,在丙杯中漂浮,则乙、丙杯中鸡蛋受到的浮力等于鸡蛋的重力,即乙、丙杯中鸡蛋排开液体的质量等于鸡蛋的质量,鸡蛋排开三种液体的质量关系为m甲ρ甲<ρ乙<ρ丙,由p=ρ液gh得,三种液体对容器底的压强大小关系是p甲7.D a在液体中漂浮,a的密度小于液体的密度,b在液体中悬浮,b的密度等于液体的密度,所以a的密度小于b的密度,故A错误;液体的密度不变,a和b的体积相同,由图可知,a排开液体的体积小于b排开液体的体积,根据F浮=ρ液gV排可知,b受到的浮力大,故B错误;液体的密度和深度相同,根据p=ρgh可知,甲、乙两容器中的液体对容器底部的压强相同,底面积相同,根据F=pS可知,容器底部受到液体的压力相同,故C错误;由于b悬浮,则b所受的浮力
F浮B=GB=,即b的重力等于排开液体的重力;a漂浮,则a所受的浮力=GA=,即a的重力等于排开液体的重力;因为两液面相平,且是同种液体,所以结合上面分析可知,两容器中液体与物体的总重力相同,即装置的总重力相同,因静止在水平桌面上,所以两容器对桌面的压力大小相等,由p=得,甲杯对桌面的压强等于乙杯对桌面的压强,故D正确。
8.0.6 0.5 60
鸡蛋受到的重力:G=mg=60×10-3 kg×10 N/kg=0.6 N;鸡蛋浸没在水中,V排=V物,鸡蛋受到的浮力:F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×5×10-5 m3=0.5 N;将鸡蛋放入容器中后,容器对地面的压力增大量:ΔF=G=0.6 N,容器底部对地面的压强增加量:Δp===60 Pa。
9.300 2.5
将金属块缓慢下降6 cm,金属块的上表面与水面相平(水未溢出),设水面上升的高度为h,金属块的体积:V金属=20 cm2×(6 cm+h)①。排开水的体积:V排=60 cm2×h②。根据V排=V金属可知,联立①②,解得h=3 cm=0.03 m,V金属=180 cm3,则金属块下降前、后容器底部受到的液体压强变化量:Δp=ρ水gh=1.0×103 kg/m3×10 N/kg×0.03 m=300 Pa;金属块下表面与水面相平时,弹簧测力计示数为4.5 N,故金属块的重力G=4.5 N,根据G=mg可知,金属块的质量:m===0.45 kg=450 g,金属块的密度ρ金属===2.5 g/cm3。
10.(1)圆柱体的体积:V=8 cm×20 cm2=160 cm3=1.6×10-4 m3,
圆柱体的质量:m=ρV=0.6×103 kg/m3×1.6×10-4 m3=0.096 kg,
圆柱体的重力:G=mg=0.096 kg×10 N/kg=0.96 N,
没加水时,圆柱体对容器底的压力:F=G=0.96 N,
圆柱体对容器底的压强:
p===480 Pa。
(2)向容器内加水,当水深为3 cm时,假设圆柱体没有浮起,则浸没的体积:
V1=20 cm2×3 cm=60 cm3=6×10-5 m3,
根据阿基米德原理可知,圆柱体所受浮力:
F浮=ρ水gV1=1.0×103 kg/m3×10 N/kg×6×10-5 m3=0.6 N<0.96 N,
所以此时圆柱体没有浮起,容器底对圆柱体的支持力:F支=G-F浮=0.96 N-0.6 N=0.36 N。
(3)继续向容器中加水,当水深为6 cm时,假设圆柱体没有浮起,则浸没的体积:
V2=2V1=2×6×10-5 m3=1.2×10-4 m3,
根据阿基米德原理可知,圆柱体所受浮力:
F浮'=ρ水gV2=1.0×103 kg/m3×10 N/kg×1.2×10-4 m3=1.2 N>0.96 N,
所以此时圆柱体漂浮,所受浮力F浮″=G=0.96 N,
排开水的体积:V排===9.6×10-5 m3=96 cm3,
圆柱体浸入水中的深度:h===4.8 cm。
基础题
1.(2021贵港)2020年11月28日上午8时30分左右,随着一阵汽笛声,在马里亚纳海沟结束科考任务的“探索一号”科考船搭载成功实现10909 m坐底纪录的“奋斗者号”胜利返航。已知海水的密度为1.03×103 kg/m3,关于“奋斗者号”在海面下下潜的过程,下列说法正确的是 ( )
A.“奋斗者号”受到海水的压强不变,受到海水的浮力不变
B.“奋斗者号”受到海水的压强变大,受到海水的浮力不变
C.“奋斗者号”受到海水的压强变大,受到海水的浮力变大
D.“奋斗者号”受到海水的压强变小,受到海水的浮力变小
2.(2021昆明)一个气球下挂一铁块置于水中某一位置静止(如图图所示)。现用手轻轻向下推一下气球,那么手离开气球后,气球和铁块的运动情况是 ( )
A.加速向下运动 B.匀速向下运动
C.减速向下运动 D.仍然处于静止状态
3.用相同木材做成的两个质量相等的长方体木块A和B,A的底面积大于B的底面积,把它们分别放入水中和酒精中,静止时如图图所示,则下列关于木块底部受到液体的压力和压强的大小关系,判断正确的是 ( )
A.FA>FB,pA
A.乙容器中木块排开的液体所受的重力大
B.木块在甲容器中时受到的浮力大
C.木块底部在乙容器中时受到的压强大
D.甲容器中盛的是A液体
5.如图图所示,“A”和“B”表示满载的轮船在海水或江水中静止时液面的位置。图中的轮船在 (选填“江水”或“海水”)中停泊。轮船满载时排开海水的质量为6000 t,则它在海水中满载时受到的浮力是 N;轮船在江水中,船底所受水的压强是6×104 Pa,船底浸入水中的深度是 。(g取10 N/kg,ρ江水=1.0×103 kg/m3,ρ海水=1.03×103 kg/m3)
能力题
6.如图图所示,将三个完全相同的鸡蛋分别放入盛有不同液体的烧杯中,鸡蛋在甲杯中沉底,在乙杯中悬浮,在丙杯中漂浮,且各杯中液体的深度相同。则下列判断中正确的是 ( )
A.三种液体的密度关系为ρ甲=ρ乙>ρ丙
B.鸡蛋排开三种液体的质量关系为m甲=m乙>m丙
C.鸡蛋受到三种液体的浮力关系为F甲
7.(2021临沂)放在水平桌面上的甲、乙两个相同的容器中盛有同种液体,体积相等的a、b两个物体在液体中静止时,两液面相平,如图图所示。则 ( )
A.物体a的密度大
B.物体b受到的浮力小
C.甲容器底部受到的压力小
D.两容器对桌面的压强一样大
8.一底面积为100 cm2的容器放在水平地面上,内盛有足量的水。现将体积为5×10-5 m3、质量为60 g的生鸡蛋放入水中,鸡蛋不断下沉,直到沉底,水未溢出,如图图所示。鸡蛋受到的重力为 N。浸没在水中时,鸡蛋受到的浮力为 N,容器底部对地面的压强增加了 Pa。(已知ρ水=1.0×103 kg/m3,g取10 N/kg)
9.如图图所示,圆柱形薄壁容器的底面积为60 cm2,弹簧测力计下挂一底面积为20 cm2的柱体金属块,金属块下表面与水面相平时,弹簧测力计的示数为4.5 N,若将金属块缓慢下降6 cm,金属块的上表面与水面相平(水未溢出),则金属块下降前、后容器底部受到液体的压强的变化量是 Pa,金属块的密度为 g/cm3。(g取10 N/kg)
10.(2021黄石)如图图所示,将密度为0.6×103 kg/m3、高度为8 cm、底面积为20 cm2的实心圆柱体竖直放在底面积为100 cm2水平放置的容器中。求:(水的密度为1.0×103 kg/m3,g取10 N/kg)
(1)没加水时,圆柱体对容器底的压强。
(2)向容器内加水,当水深为3 cm时,容器底对圆柱体的支持力。
(3)继续向容器中加水,当水深为6 cm,圆柱体竖直静止时,圆柱体浸入水中的深度。
答案
压强和浮力的综合应用
1.B “奋斗者号”下潜的过程中,所处深度h增大,海水的密度不变,由p=ρgh可知,它受到的压强变大,“奋斗者号”没入海水中后,下潜的过程中,排开海水的体积V排不变,由于海水的密度不变,则根据F浮=ρ液gV排可知,受到的浮力不变,故B正确。
2.A 由图可知,气球和铁块处于静止状态,受到的浮力等于总的重力,现用手轻轻向下推一下气球,气球所处深度增加,压强增大,气球体积减小,排开液体的体积减小,浮力减小,且小于重力,那么手离开气球后,气球和铁块会加速向下运动,故A正确。
3.D A和B的质量相同,根据G=mg可知,它们的重力相同;A和B在液体中都处于漂浮状态,故所受浮力和重力大小相等,都为F浮=G;浮力产生的原因为上、下表面的压力差,A、B上表面不受液体压力,故A、B下表面所受的液体压力都等于所受浮力的大小,即FA=FB=
F浮;A的底面积大于B的底面积,根据p=可知,木块底部受到液体的压强pA
5.海水 6×107 6 m
在海水和江水中,轮船都漂浮,浮力和自身的重力大小相等,即浮力大小不变;因海水的密度大于江水的密度,则根据公式F浮=ρ液gV排可知,轮船排开海水的体积小于排开江水的体积,即轮船在海水中的吃水线高度较低,所以图中的轮船是在海水中停泊的;根据阿基米德原理得,轮船所受的浮力:F浮=G排=m排g=6000×103 kg×10 N/kg=6×107 N;由液体压强公式p=ρgh得,船底浸入江水中的深度:h===6 m。
6.C 鸡蛋在甲杯中沉底,甲杯液体的密度小于鸡蛋的密度;在乙杯中悬浮,乙杯液体的密度等于鸡蛋的密度;在丙杯中漂浮,丙杯液体的密度大于鸡蛋的密度,三种液体的密度关系为ρ甲<ρ乙<ρ丙,故A错误。鸡蛋在甲杯中沉底,浮力小于鸡蛋的重力,则排开液体的质量小于鸡蛋的质量;在乙杯中悬浮,在丙杯中漂浮,则乙、丙杯中鸡蛋受到的浮力等于鸡蛋的重力,即乙、丙杯中鸡蛋排开液体的质量等于鸡蛋的质量,鸡蛋排开三种液体的质量关系为m甲
F浮B=GB=,即b的重力等于排开液体的重力;a漂浮,则a所受的浮力=GA=,即a的重力等于排开液体的重力;因为两液面相平,且是同种液体,所以结合上面分析可知,两容器中液体与物体的总重力相同,即装置的总重力相同,因静止在水平桌面上,所以两容器对桌面的压力大小相等,由p=得,甲杯对桌面的压强等于乙杯对桌面的压强,故D正确。
8.0.6 0.5 60
鸡蛋受到的重力:G=mg=60×10-3 kg×10 N/kg=0.6 N;鸡蛋浸没在水中,V排=V物,鸡蛋受到的浮力:F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×5×10-5 m3=0.5 N;将鸡蛋放入容器中后,容器对地面的压力增大量:ΔF=G=0.6 N,容器底部对地面的压强增加量:Δp===60 Pa。
9.300 2.5
将金属块缓慢下降6 cm,金属块的上表面与水面相平(水未溢出),设水面上升的高度为h,金属块的体积:V金属=20 cm2×(6 cm+h)①。排开水的体积:V排=60 cm2×h②。根据V排=V金属可知,联立①②,解得h=3 cm=0.03 m,V金属=180 cm3,则金属块下降前、后容器底部受到的液体压强变化量:Δp=ρ水gh=1.0×103 kg/m3×10 N/kg×0.03 m=300 Pa;金属块下表面与水面相平时,弹簧测力计示数为4.5 N,故金属块的重力G=4.5 N,根据G=mg可知,金属块的质量:m===0.45 kg=450 g,金属块的密度ρ金属===2.5 g/cm3。
10.(1)圆柱体的体积:V=8 cm×20 cm2=160 cm3=1.6×10-4 m3,
圆柱体的质量:m=ρV=0.6×103 kg/m3×1.6×10-4 m3=0.096 kg,
圆柱体的重力:G=mg=0.096 kg×10 N/kg=0.96 N,
没加水时,圆柱体对容器底的压力:F=G=0.96 N,
圆柱体对容器底的压强:
p===480 Pa。
(2)向容器内加水,当水深为3 cm时,假设圆柱体没有浮起,则浸没的体积:
V1=20 cm2×3 cm=60 cm3=6×10-5 m3,
根据阿基米德原理可知,圆柱体所受浮力:
F浮=ρ水gV1=1.0×103 kg/m3×10 N/kg×6×10-5 m3=0.6 N<0.96 N,
所以此时圆柱体没有浮起,容器底对圆柱体的支持力:F支=G-F浮=0.96 N-0.6 N=0.36 N。
(3)继续向容器中加水,当水深为6 cm时,假设圆柱体没有浮起,则浸没的体积:
V2=2V1=2×6×10-5 m3=1.2×10-4 m3,
根据阿基米德原理可知,圆柱体所受浮力:
F浮'=ρ水gV2=1.0×103 kg/m3×10 N/kg×1.2×10-4 m3=1.2 N>0.96 N,
所以此时圆柱体漂浮,所受浮力F浮″=G=0.96 N,
排开水的体积:V排===9.6×10-5 m3=96 cm3,
圆柱体浸入水中的深度:h===4.8 cm。
