小学数学北师大版五年级上四第5课《探索活动:梯形的面积》课件(共15张PPT)
文档属性
| 名称 | 小学数学北师大版五年级上四第5课《探索活动:梯形的面积》课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 11:16:20 | ||
图片预览



文档简介
(共15张PPT)
第5课 探索活动:
梯形的面积
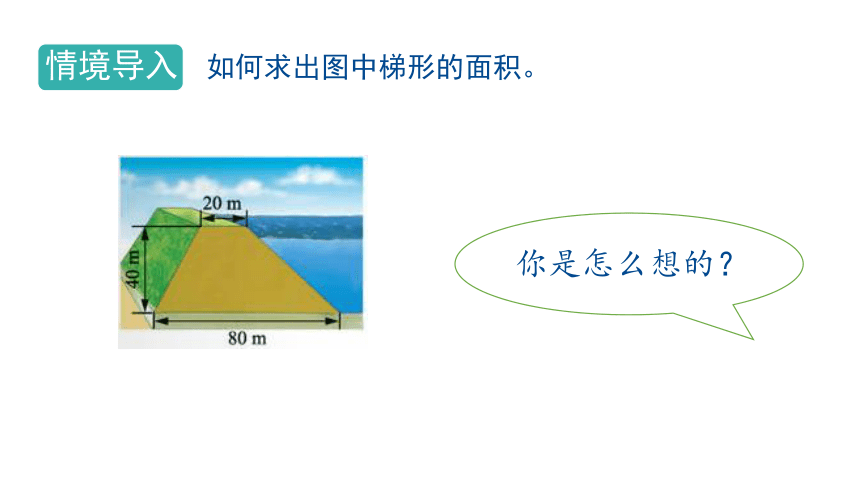
如何求出图中梯形的面积。
你是怎么想的?
情境导入
与同伴说一说你的想法。
通过比较转化前后图形之间的关系推导计算方法。
可以把梯形转化为以前学过的图形。
探究新知
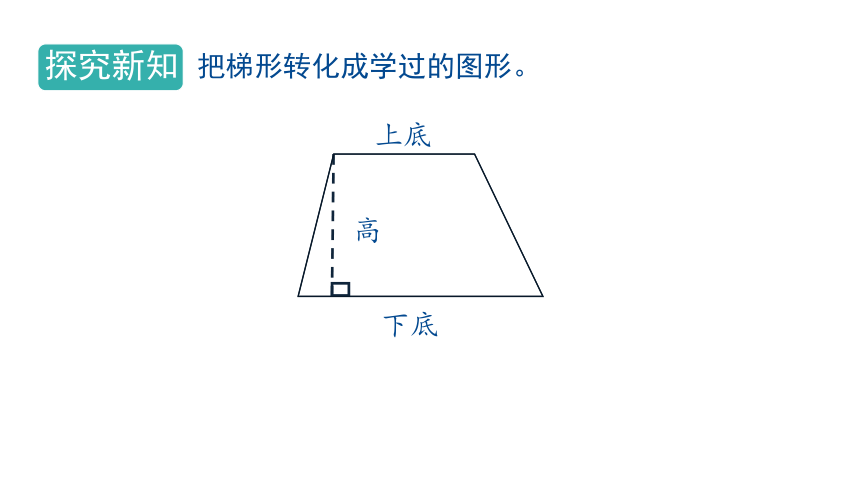
上底
下底
高
把梯形转化成学过的图形。
探究新知
把梯形转化成学过的图形。
中位线
探究新知
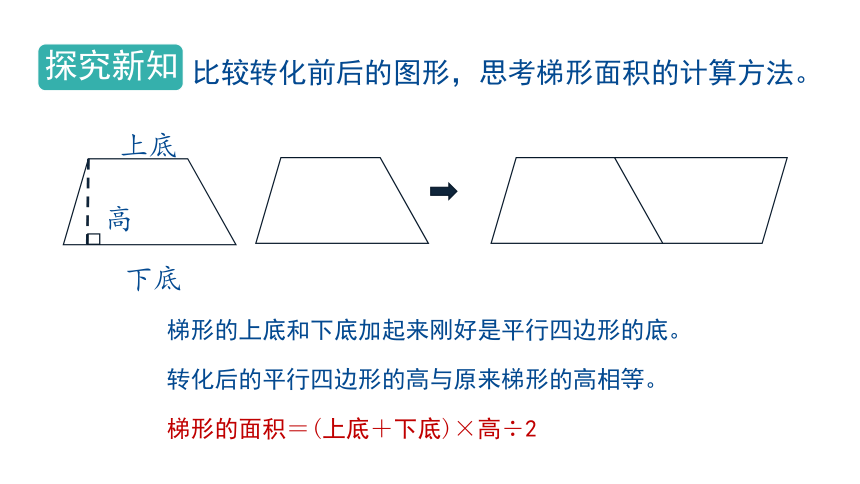
比较转化前后的图形,思考梯形面积的计算方法。
上底
下底
高
梯形的上底和下底加起来刚好是平行四边形的底。
转化后的平行四边形的高与原来梯形的高相等。
梯形的面积=(上底+下底)×高÷2
探究新知
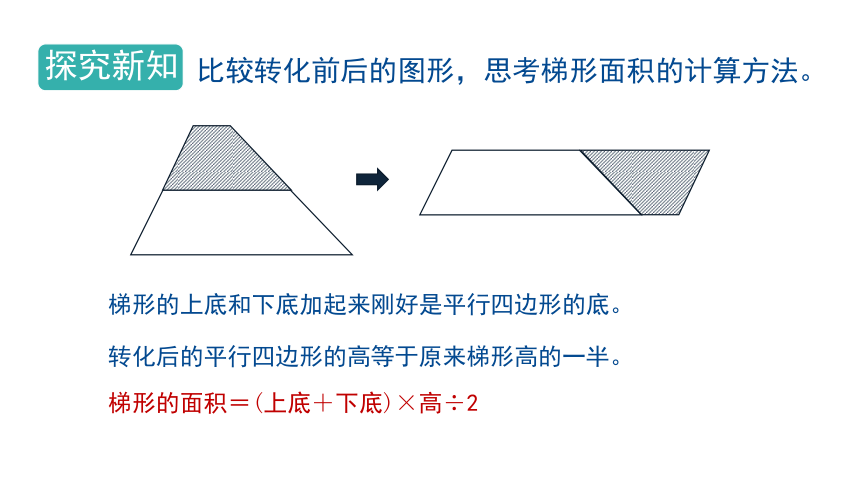
比较转化前后的图形,思考梯形面积的计算方法。
梯形的上底和下底加起来刚好是平行四边形的底。
转化后的平行四边形的高等于原来梯形高的一半。
梯形的面积=(上底+下底)×高÷2
探究新知
字母公式
如果用S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,那么,梯形的面积公式可以写成:
S=
(a+b)h÷2
探究新知
你能求出堤坝横截面的面积吗?
(20+80)×40÷2
=4000÷2
=2000(㎡)
探究新知
1.计算下列梯形的面积。
(1) (2)
思路分析:找到每个梯形的上底、下底和高,利用“梯形的面积=(上底+下底)×高÷2”可以直接求得梯形的面积。
正确解答:
(8+12)×10÷2=100(cm2)
正确解答:
(16+20)×10÷2=180(dm2)
2.一条新挖的水渠,横截面是一个梯形(如图所示)。
它的横截面的面积是多少?
思路分析:上底为1.4 m,下底为2.8 m,高为1.2 m,利用梯形的面积计算公式可求出横截面的面积。
正确解答:
(1.4+2.8)×1.2÷2=2.52(m2)
答:它的横截面的面积是2.52平方米。
3.如下图,庆达钢管厂把生产的钢管堆成了一个梯形,这堆钢管一共有多少根?
思路分析:先数出第一层有6根钢管,看成梯形的上底,最下面一层有15根钢管,看成梯形的下底,一共有15-6+1=10(层),看成梯形的高,再利用梯形的面积计算公式求出这堆钢管一共有(6+15)×10÷2=105(根)。
正确解答:
15-6+1=10(层)
(6+15)×10÷2=105(根)
答:这堆钢管一共有105根。
4.如下图,已知阴影部分的面积是72 cm2,求梯形的面积
思路分析:先根据阴影三角形的面积是72 cm2和底是18 cm,可求出阴影三角形的高是72×2÷18=8(cm),这个高也是梯形的高。再根据“梯形的面积=(上底+下底)×高÷2”,可求出梯形的面积是(7+18)×8÷2=100(cm2)。
正确解答:
72×2÷18=8(cm)
(7+18)×8÷2=100(cm2)
答:梯形的面积是100平方厘米。
5.王大伯靠一面墙用篱笆围了一个面积是96 m2的直角梯形养鸡场(如下图所示),围成这个养鸡场至少需要多少米篱笆?
思路分析:这个养鸡场的形状是梯形,要想求围成这个养鸡场至少需要多少米篱笆,就是求梯形上底、下底、高的长度和。高已知,需要求上底、下底的长度和,利用“(上底+下底)=梯形的面积×2÷高”,求出上底、下底的长度和为96×2÷6=32(m),再加上高的长度6 m,求出围成这个养鸡场至少需要32+6=38(m)篱笆。
正确解答:
96×2÷6=32(m)
6+32=38(m)
答:围成这个养鸡场至少需要38米篱笆。
6.下面是一个直角梯形,它的上底是25 dm,如果下底减少15 dm,那么这个直角梯形就变成了一个正方形。求这个直角梯形的面积。
思路分析:由下底减少15 dm,这个直角梯形就变成了一个正方形可知,这个直角梯形的下底比上底长15 dm,下底是25+15=40(dm),高和上底一样长,是25 dm。根据梯形的面积计算公式,可以计算出这个直角梯形的面积是(25+40)×25÷2=812.5(dm2)。
正确解答:
25+15=40(dm)
(25+40)×25÷2=812.5(dm2)
答:这个直角梯形的面积是812.5平方分米。
第5课 探索活动:
梯形的面积
如何求出图中梯形的面积。
你是怎么想的?
情境导入
与同伴说一说你的想法。
通过比较转化前后图形之间的关系推导计算方法。
可以把梯形转化为以前学过的图形。
探究新知
上底
下底
高
把梯形转化成学过的图形。
探究新知
把梯形转化成学过的图形。
中位线
探究新知
比较转化前后的图形,思考梯形面积的计算方法。
上底
下底
高
梯形的上底和下底加起来刚好是平行四边形的底。
转化后的平行四边形的高与原来梯形的高相等。
梯形的面积=(上底+下底)×高÷2
探究新知
比较转化前后的图形,思考梯形面积的计算方法。
梯形的上底和下底加起来刚好是平行四边形的底。
转化后的平行四边形的高等于原来梯形高的一半。
梯形的面积=(上底+下底)×高÷2
探究新知
字母公式
如果用S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,那么,梯形的面积公式可以写成:
S=
(a+b)h÷2
探究新知
你能求出堤坝横截面的面积吗?
(20+80)×40÷2
=4000÷2
=2000(㎡)
探究新知
1.计算下列梯形的面积。
(1) (2)
思路分析:找到每个梯形的上底、下底和高,利用“梯形的面积=(上底+下底)×高÷2”可以直接求得梯形的面积。
正确解答:
(8+12)×10÷2=100(cm2)
正确解答:
(16+20)×10÷2=180(dm2)
2.一条新挖的水渠,横截面是一个梯形(如图所示)。
它的横截面的面积是多少?
思路分析:上底为1.4 m,下底为2.8 m,高为1.2 m,利用梯形的面积计算公式可求出横截面的面积。
正确解答:
(1.4+2.8)×1.2÷2=2.52(m2)
答:它的横截面的面积是2.52平方米。
3.如下图,庆达钢管厂把生产的钢管堆成了一个梯形,这堆钢管一共有多少根?
思路分析:先数出第一层有6根钢管,看成梯形的上底,最下面一层有15根钢管,看成梯形的下底,一共有15-6+1=10(层),看成梯形的高,再利用梯形的面积计算公式求出这堆钢管一共有(6+15)×10÷2=105(根)。
正确解答:
15-6+1=10(层)
(6+15)×10÷2=105(根)
答:这堆钢管一共有105根。
4.如下图,已知阴影部分的面积是72 cm2,求梯形的面积
思路分析:先根据阴影三角形的面积是72 cm2和底是18 cm,可求出阴影三角形的高是72×2÷18=8(cm),这个高也是梯形的高。再根据“梯形的面积=(上底+下底)×高÷2”,可求出梯形的面积是(7+18)×8÷2=100(cm2)。
正确解答:
72×2÷18=8(cm)
(7+18)×8÷2=100(cm2)
答:梯形的面积是100平方厘米。
5.王大伯靠一面墙用篱笆围了一个面积是96 m2的直角梯形养鸡场(如下图所示),围成这个养鸡场至少需要多少米篱笆?
思路分析:这个养鸡场的形状是梯形,要想求围成这个养鸡场至少需要多少米篱笆,就是求梯形上底、下底、高的长度和。高已知,需要求上底、下底的长度和,利用“(上底+下底)=梯形的面积×2÷高”,求出上底、下底的长度和为96×2÷6=32(m),再加上高的长度6 m,求出围成这个养鸡场至少需要32+6=38(m)篱笆。
正确解答:
96×2÷6=32(m)
6+32=38(m)
答:围成这个养鸡场至少需要38米篱笆。
6.下面是一个直角梯形,它的上底是25 dm,如果下底减少15 dm,那么这个直角梯形就变成了一个正方形。求这个直角梯形的面积。
思路分析:由下底减少15 dm,这个直角梯形就变成了一个正方形可知,这个直角梯形的下底比上底长15 dm,下底是25+15=40(dm),高和上底一样长,是25 dm。根据梯形的面积计算公式,可以计算出这个直角梯形的面积是(25+40)×25÷2=812.5(dm2)。
正确解答:
25+15=40(dm)
(25+40)×25÷2=812.5(dm2)
答:这个直角梯形的面积是812.5平方分米。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
