复习圆柱的表面积课件六年级下册数学人教版(共31张PPT)
文档属性
| 名称 | 复习圆柱的表面积课件六年级下册数学人教版(共31张PPT) | 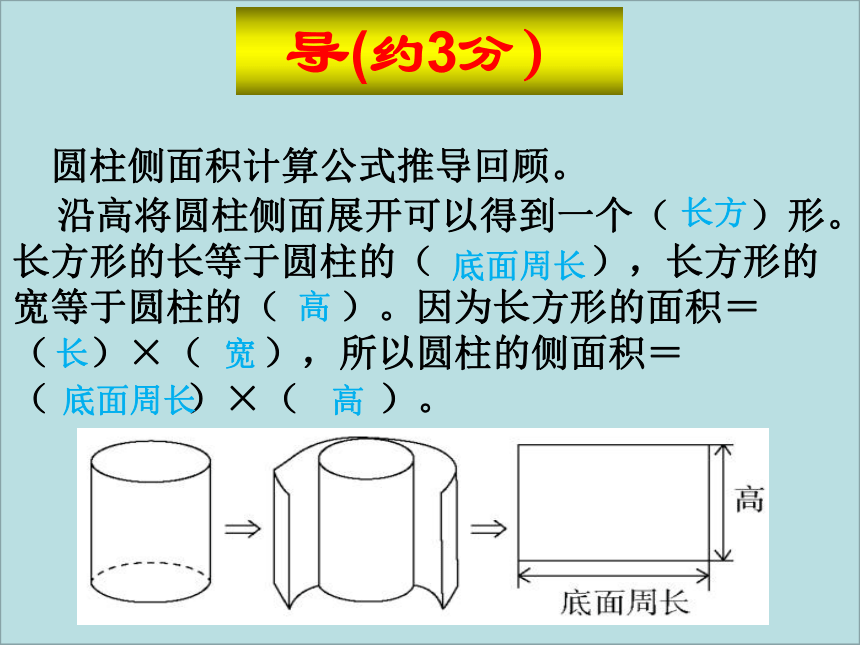 | |
| 格式 | pptx | ||
| 文件大小 | 13.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 11:55:30 | ||
图片预览












文档简介
(共31张PPT)
导(约3分)
圆柱侧面积计算公式推导回顾。
沿高将圆柱侧面展开可以得到一个( )形。长方形的长等于圆柱的( ),长方形的宽等于圆柱的( )。因为长方形的面积=( )×( ),所以圆柱的侧面积= ( )×( )。
长方
底面周长
高
长
宽
底面周长
高
复习圆柱的
表面积
复习目标:
1.通过复习,进一步掌握圆柱的侧面积和表面积的计算方法。
2.能利用公式灵活解决生活中的实际问题。
重难点:
重点:熟练掌握圆柱的侧面积和表面积的计算方法。
难点:能利用公式灵活解决生活中的实际问题。
思(约13分)
结合以下提示,认真思考并独立完成导学案上的习题。
1.勾画出关键词语,判断是求哪几个面的面积?
2.利用哪个计算公式?
3.根据题意,只列式不计算。
要求:认真书写,深入思考,独立完成各小题并认真检查,有疑惑的地方作出标记。
议(约7分)
结合所学内容,重点讨论解题方法和思路:
对议:基础训练1.2
能力提升1. 2. 3. 4
组议:知识拓展1.2.3
要求:全员参与,组长合理分工,大号发言,小号补充。
展(约13分)
要求:
1.展示语言要规范,声音洪亮;
2.主动展示,做到大胆、大方、大声;
3.发现问题,其他成员要敢于大胆质疑;
4.认真做好笔记。
基础训练
1.求下面圆柱的表面积,只列式不计算。
(1) r=2cm h=1cm
(2) d=2dm h=3dm
(3) c=6.28cm h=2cm
基础训练
2.判断
(1)圆柱的侧面展开是一个正方形,那么它的直径和高相等。 ( )
(2)圆柱的侧面积等于底面积×高。 ( )
(3)圆柱的侧面沿高展开可以得到一个长方形或正方形。 ( )
(4)求做一个圆柱形油桶需要多少铁皮,就是求圆柱的表面积。( )
√
X
√
X
能力提升
(1)0.2 X 3.14 X 10 =6.28(米)
答:前进的路程是6.28米。
1. 一台压路机的滚筒宽2米,直径为0.2米。如果它滚动10周
(1)前进的路程是多少米?
(2)压路的面积是多少平方米?
(2)6.28 X 2 =12.56(平方米)
答:压路的面积是12.56平方米。
能力提升
2.在一个圆柱形水池的底面和四周抹水泥,水池底面半径是8 m,池深2 m,抹水泥的面积是多少平方米?
3.14×82+2×3.14×8×2=301.44 (m2)
答:抹水泥的面积是301.44 m2。
能力提升
3. 一个圆柱形的铁皮水桶,底面直径是4分米,高是4.5分米,为了防止生锈,要在水桶里外两面都涂上防锈漆,涂漆的 面积是多少平方分米?
4 ÷2=2(分米)
(3.14 X 2 + 3.14 X 4 X4.5) X 2
=138.16(平方分米)
答:涂漆的面积是138.16平方分米。
2
能力提升
4. 用铁皮制作20节圆柱形通风管,每节长60 cm,底面半径是15 cm,至少需要多少平方米铁皮?(保留两位小数)
2×3.14×15×60×20=113040 (cm2)
113040 cm2=11.3040 m2≈11.31 m2
答:至少需要11.31 m2铁皮。
知识拓展
1.一根圆柱形木材长20分米,底面半径是10厘米,把它截成4个相等的圆柱体,表面积增加了多少平方厘米?
3.14 X 10 X 6 =1884 (平方厘米)
答:表面积增加了1884平方厘米。
2
知识拓展
2.一个底面半径3厘米,高8厘米的圆柱,如果沿底面直径把它平均分成两半,它的表面积增加了多少平方厘米?
3 x 2 x 8 x 2=96(平方厘米)
答:它的表面积增加了96平方厘米。
在解决“求圆柱表面积”的有关问题时,要注意弄清题中要求的到底是哪部分的面积。一般分为3种情况:
1、有两个底面,一个侧面。
2、只有一个底面和一个侧面。
3、两个底面都没有,只需计算侧面积的。
在解答这些问题时,具体情况要具体对待。
评(约5分)
例:饼干盒、茶叶筒等
例:无盖水桶、圆柱形鱼缸等。
例:水管、烟囱等。
联系生活实际,说说生活中的这些问题是求哪些面积?
⑴圆柱形水池的占地面积。
⑵做一节烟囱所需铁皮面积。
⑶求易拉罐上商标纸的面积。
⑷做茶叶筒所需铁皮面积。
⑸做一个无盖水桶所需铁皮面积。
⑹压路机的滚筒转动一周,求压路面积。
检(约3分)
知识拓展
3.如图,有一张长方形铁皮,剪下阴影部分围成一个圆柱,求这个圆柱的表面积。
圆柱的底面直径为:
18.84÷3.14=6 (dm)
圆柱的高为:10-6=4 (dm)
圆柱的表面积为:
3.14×(6÷2)×2+3.14×6×4=131.88 (dm )
答:这个圆柱的表面积是131.88 dm 。
2
2
2
横切
纵切
(1)横切成两个圆柱,表面积之和发生了什么变化?
横切成3个圆柱呢?
(2)一个圆柱从底面圆心纵切成两半,表面积之和
发生了什么变化?
13.求下面各图形的表面积。
(10×10)×2+(10×15)×4
=100×2+150×4
=200+600
=800(cm2)
13.求下面各图形的表面积。
62×6
=36×6
=216(cm2)
13.求下面各图形的表面积。
3.14×52×2+2×3.14×5×12
=3.14×50+3.14×120
=157+367.8
=533.8(cm2)
有没有更加简便的计算方法?
πr2×2+2πr×h
=2πr2+2πr×h
=2πr×r+2πr×h
=2πr×(r+h)
底面周长×(半径+高)
2×3.14×5×(5+12)
=3.14×10×17
=3.14×170
=533.8(cm2)
13.求下面各图形的表面积。
= 2πr×(r+h)
圆柱表面积=底面周长×(半径+高)
= C×(C÷π÷2+h)
(1)花布的面积(侧面积):
3.14×18×80
=56.52×80
=4521.6(cm2)
(2)黄布的面积(两个底面积):
3.14×(18÷2)2×2
=254.34×2
=508.68(cm2)
答:花布需要4521.6平方厘米,黄布需要508.68平方厘米。
3.14×3.5×12
=3.14×42
=131.88(cm2)
答:制作中间的轴需要131.88cm2的硬纸板。
提示:求彩纸的面积就是用灯笼的表面积减去两个78.5㎝2
(1)侧面积:3.14×20×30=1884(cm)2
(2)底面积:3.14×(20 ÷2)2×2=628(cm)2
(3)彩纸的面积:1884+628-78.5×2=2355(cm)2
答:他用了2355平方厘米的彩纸。
(1)底面直径:
(2)铁皮面积:
3.14×(9÷2)2+3.14×9×12
=63.585+339.12
=402.705(dm2)
答:做这个水桶大约要用402.705dm2铁皮。
188.4÷(2×3.14×2)
=188.4÷12.56
=15(dm)
答:它的高是15dm。
导(约3分)
圆柱侧面积计算公式推导回顾。
沿高将圆柱侧面展开可以得到一个( )形。长方形的长等于圆柱的( ),长方形的宽等于圆柱的( )。因为长方形的面积=( )×( ),所以圆柱的侧面积= ( )×( )。
长方
底面周长
高
长
宽
底面周长
高
复习圆柱的
表面积
复习目标:
1.通过复习,进一步掌握圆柱的侧面积和表面积的计算方法。
2.能利用公式灵活解决生活中的实际问题。
重难点:
重点:熟练掌握圆柱的侧面积和表面积的计算方法。
难点:能利用公式灵活解决生活中的实际问题。
思(约13分)
结合以下提示,认真思考并独立完成导学案上的习题。
1.勾画出关键词语,判断是求哪几个面的面积?
2.利用哪个计算公式?
3.根据题意,只列式不计算。
要求:认真书写,深入思考,独立完成各小题并认真检查,有疑惑的地方作出标记。
议(约7分)
结合所学内容,重点讨论解题方法和思路:
对议:基础训练1.2
能力提升1. 2. 3. 4
组议:知识拓展1.2.3
要求:全员参与,组长合理分工,大号发言,小号补充。
展(约13分)
要求:
1.展示语言要规范,声音洪亮;
2.主动展示,做到大胆、大方、大声;
3.发现问题,其他成员要敢于大胆质疑;
4.认真做好笔记。
基础训练
1.求下面圆柱的表面积,只列式不计算。
(1) r=2cm h=1cm
(2) d=2dm h=3dm
(3) c=6.28cm h=2cm
基础训练
2.判断
(1)圆柱的侧面展开是一个正方形,那么它的直径和高相等。 ( )
(2)圆柱的侧面积等于底面积×高。 ( )
(3)圆柱的侧面沿高展开可以得到一个长方形或正方形。 ( )
(4)求做一个圆柱形油桶需要多少铁皮,就是求圆柱的表面积。( )
√
X
√
X
能力提升
(1)0.2 X 3.14 X 10 =6.28(米)
答:前进的路程是6.28米。
1. 一台压路机的滚筒宽2米,直径为0.2米。如果它滚动10周
(1)前进的路程是多少米?
(2)压路的面积是多少平方米?
(2)6.28 X 2 =12.56(平方米)
答:压路的面积是12.56平方米。
能力提升
2.在一个圆柱形水池的底面和四周抹水泥,水池底面半径是8 m,池深2 m,抹水泥的面积是多少平方米?
3.14×82+2×3.14×8×2=301.44 (m2)
答:抹水泥的面积是301.44 m2。
能力提升
3. 一个圆柱形的铁皮水桶,底面直径是4分米,高是4.5分米,为了防止生锈,要在水桶里外两面都涂上防锈漆,涂漆的 面积是多少平方分米?
4 ÷2=2(分米)
(3.14 X 2 + 3.14 X 4 X4.5) X 2
=138.16(平方分米)
答:涂漆的面积是138.16平方分米。
2
能力提升
4. 用铁皮制作20节圆柱形通风管,每节长60 cm,底面半径是15 cm,至少需要多少平方米铁皮?(保留两位小数)
2×3.14×15×60×20=113040 (cm2)
113040 cm2=11.3040 m2≈11.31 m2
答:至少需要11.31 m2铁皮。
知识拓展
1.一根圆柱形木材长20分米,底面半径是10厘米,把它截成4个相等的圆柱体,表面积增加了多少平方厘米?
3.14 X 10 X 6 =1884 (平方厘米)
答:表面积增加了1884平方厘米。
2
知识拓展
2.一个底面半径3厘米,高8厘米的圆柱,如果沿底面直径把它平均分成两半,它的表面积增加了多少平方厘米?
3 x 2 x 8 x 2=96(平方厘米)
答:它的表面积增加了96平方厘米。
在解决“求圆柱表面积”的有关问题时,要注意弄清题中要求的到底是哪部分的面积。一般分为3种情况:
1、有两个底面,一个侧面。
2、只有一个底面和一个侧面。
3、两个底面都没有,只需计算侧面积的。
在解答这些问题时,具体情况要具体对待。
评(约5分)
例:饼干盒、茶叶筒等
例:无盖水桶、圆柱形鱼缸等。
例:水管、烟囱等。
联系生活实际,说说生活中的这些问题是求哪些面积?
⑴圆柱形水池的占地面积。
⑵做一节烟囱所需铁皮面积。
⑶求易拉罐上商标纸的面积。
⑷做茶叶筒所需铁皮面积。
⑸做一个无盖水桶所需铁皮面积。
⑹压路机的滚筒转动一周,求压路面积。
检(约3分)
知识拓展
3.如图,有一张长方形铁皮,剪下阴影部分围成一个圆柱,求这个圆柱的表面积。
圆柱的底面直径为:
18.84÷3.14=6 (dm)
圆柱的高为:10-6=4 (dm)
圆柱的表面积为:
3.14×(6÷2)×2+3.14×6×4=131.88 (dm )
答:这个圆柱的表面积是131.88 dm 。
2
2
2
横切
纵切
(1)横切成两个圆柱,表面积之和发生了什么变化?
横切成3个圆柱呢?
(2)一个圆柱从底面圆心纵切成两半,表面积之和
发生了什么变化?
13.求下面各图形的表面积。
(10×10)×2+(10×15)×4
=100×2+150×4
=200+600
=800(cm2)
13.求下面各图形的表面积。
62×6
=36×6
=216(cm2)
13.求下面各图形的表面积。
3.14×52×2+2×3.14×5×12
=3.14×50+3.14×120
=157+367.8
=533.8(cm2)
有没有更加简便的计算方法?
πr2×2+2πr×h
=2πr2+2πr×h
=2πr×r+2πr×h
=2πr×(r+h)
底面周长×(半径+高)
2×3.14×5×(5+12)
=3.14×10×17
=3.14×170
=533.8(cm2)
13.求下面各图形的表面积。
= 2πr×(r+h)
圆柱表面积=底面周长×(半径+高)
= C×(C÷π÷2+h)
(1)花布的面积(侧面积):
3.14×18×80
=56.52×80
=4521.6(cm2)
(2)黄布的面积(两个底面积):
3.14×(18÷2)2×2
=254.34×2
=508.68(cm2)
答:花布需要4521.6平方厘米,黄布需要508.68平方厘米。
3.14×3.5×12
=3.14×42
=131.88(cm2)
答:制作中间的轴需要131.88cm2的硬纸板。
提示:求彩纸的面积就是用灯笼的表面积减去两个78.5㎝2
(1)侧面积:3.14×20×30=1884(cm)2
(2)底面积:3.14×(20 ÷2)2×2=628(cm)2
(3)彩纸的面积:1884+628-78.5×2=2355(cm)2
答:他用了2355平方厘米的彩纸。
(1)底面直径:
(2)铁皮面积:
3.14×(9÷2)2+3.14×9×12
=63.585+339.12
=402.705(dm2)
答:做这个水桶大约要用402.705dm2铁皮。
188.4÷(2×3.14×2)
=188.4÷12.56
=15(dm)
答:它的高是15dm。
