人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》课件
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 13:33:17 | ||
图片预览






文档简介
(共17张PPT)
函数的奇偶性
我们生活在美的世界中,有过许多对美的感受,如和谐美、自然美、对称美……下面图片给我们什么感觉呢?
将上面两组图像变成函数的形式放在直角坐标系中,观察它们是否也有对称性呢?
x
y
O
1
-1
-x
x
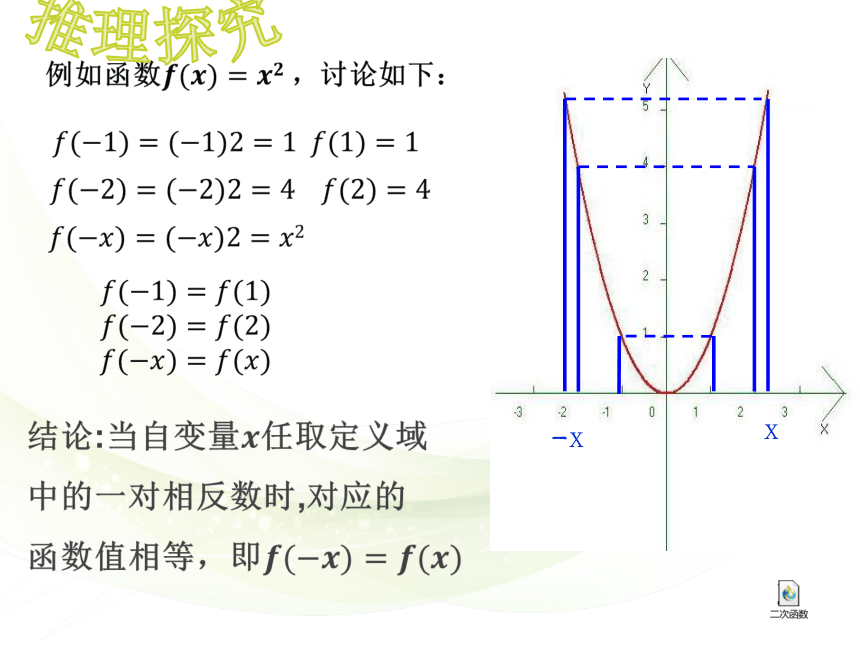
结论:当自变量任取定义域中的两个相反数时,对应的函数值也互为相反数,即f(-x)=-f(x)
函数奇偶性的定义:
对于奇、偶函数定义的几点说明:
(2) 定义域关于原点对称是函数具有奇偶性的先决条件。
(4)函数的奇偶性与最值都是在整个定义域上的性质, 是“整体性质”,而函数的单调性是在函数定义域或其子集上的性质,是“局部”性质。
奇函数与偶函数的性质
说出下列函数的奇偶性:
奇函数
奇函数
奇函数
奇函数
偶函数
偶函数
例1. 判断下列函数的奇偶性
说明:用定义判断函数奇偶性的步骤:
⑴先求出定义域,看定义域是否关于原点对称。
x
y
0
1
2
-1
解: 定义域为 [0 ,+∞)
∵ 定义域不关于原点对称
∴f(x)为非奇非偶函数
思考2:以下函数是奇函数吗?是偶函数 吗?
思考3:
在前面的几个函数中有的是奇函数,有的是偶函数,也有非奇非偶函数。那么有没有这样的函数,它既是奇函数又是偶函数呢?
x
y
0
1
-1
奇函数
偶函数
既奇又偶函数
非奇非偶函数
函数的分类
课堂小结:
两个步骤:(判断函数的奇偶性)
课外思考题:
A. 奇函数 B. 偶函数
C. 非奇非偶 D. 既是奇又是偶函数
A. 奇函数 B. 偶函数
C. 非奇非偶 D. 既是奇又是偶函数
函数的奇偶性
我们生活在美的世界中,有过许多对美的感受,如和谐美、自然美、对称美……下面图片给我们什么感觉呢?
将上面两组图像变成函数的形式放在直角坐标系中,观察它们是否也有对称性呢?
x
y
O
1
-1
-x
x
结论:当自变量任取定义域中的两个相反数时,对应的函数值也互为相反数,即f(-x)=-f(x)
函数奇偶性的定义:
对于奇、偶函数定义的几点说明:
(2) 定义域关于原点对称是函数具有奇偶性的先决条件。
(4)函数的奇偶性与最值都是在整个定义域上的性质, 是“整体性质”,而函数的单调性是在函数定义域或其子集上的性质,是“局部”性质。
奇函数与偶函数的性质
说出下列函数的奇偶性:
奇函数
奇函数
奇函数
奇函数
偶函数
偶函数
例1. 判断下列函数的奇偶性
说明:用定义判断函数奇偶性的步骤:
⑴先求出定义域,看定义域是否关于原点对称。
x
y
0
1
2
-1
解: 定义域为 [0 ,+∞)
∵ 定义域不关于原点对称
∴f(x)为非奇非偶函数
思考2:以下函数是奇函数吗?是偶函数 吗?
思考3:
在前面的几个函数中有的是奇函数,有的是偶函数,也有非奇非偶函数。那么有没有这样的函数,它既是奇函数又是偶函数呢?
x
y
0
1
-1
奇函数
偶函数
既奇又偶函数
非奇非偶函数
函数的分类
课堂小结:
两个步骤:(判断函数的奇偶性)
课外思考题:
A. 奇函数 B. 偶函数
C. 非奇非偶 D. 既是奇又是偶函数
A. 奇函数 B. 偶函数
C. 非奇非偶 D. 既是奇又是偶函数
