人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》 课件(共15张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
2.1.4函数的奇偶性
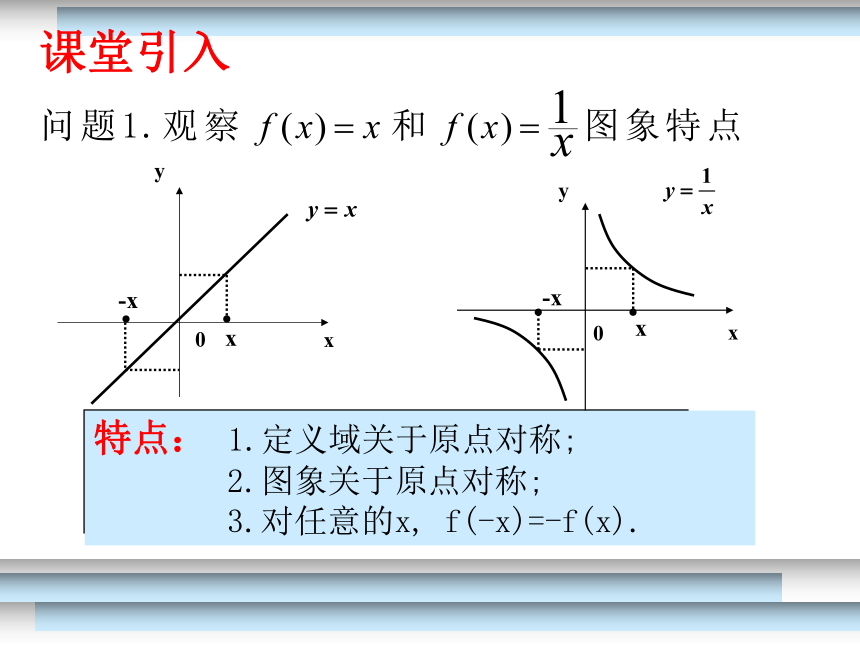
特点: 1.定义域关于原点对称;
2.图象关于原点对称;
3.对任意的x, f(-x)=-f(x).
课堂引入
x
0
y
y
x
0
●
●
-x
x
-x
x
●
●
设y=f(x)的定义域为D,对于函数定义域D内的任意一个x都有-x∈D,且
那么y=f(x)叫奇函数.
f(-x)=-f(x)
奇函数定义
奇函数的图象关于原点对称
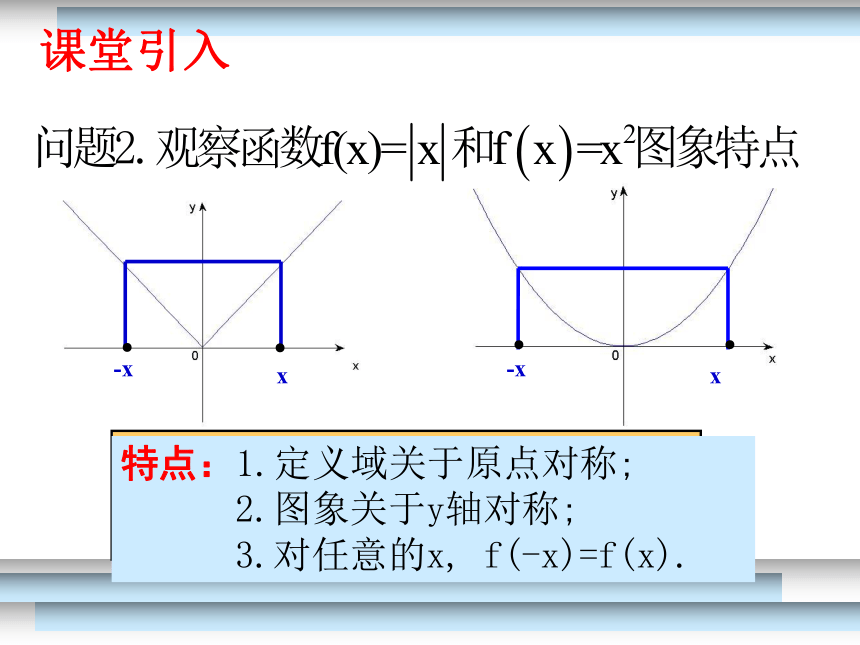
特点:1.定义域关于原点对称;
2.图象关于y轴对称;
3.对任意的x, f(-x)=f(x).
课堂引入
-x
x
●
●
-x
x
●
●
偶函数定义
设y=f(x)的定义域为D,对于函数定义域D内的任意一个x都有-x∈D,且
那么y=f(x)叫偶函数.
f(-x)=f(x)
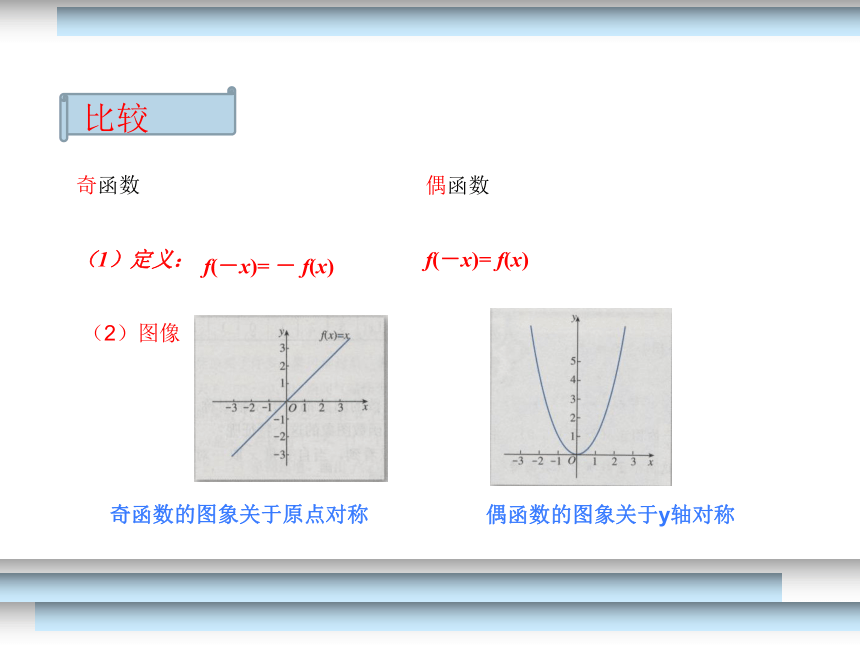
比较
奇函数
偶函数
(1)定义:
f(-x)= f(x)
(2)图像
f(-x)= - f(x)
奇函数的图象关于原点对称
偶函数的图象关于y轴对称
1、若函数f(x) 在区间[3-a,5]上是奇函数,则a的值是( )
思考
2、已知f(x) =x5+ax3+bx,若f(-2)=10,求f(2)=( )
0
y
x
y
x
⑴
⑵
小结: 图象法判断函数的奇偶性
练 习 判断下列函数的奇偶性
0
f(x)
g(x)
定义法判断函数的奇偶性:
3.利用定义判断函数奇偶性的格式步骤
1)首先确定函数的定义域,并判断其定义域是否关于原点对称;(如果定义域不关于原点对称,则函数非奇非偶,下面的步骤就不用)
2)确定f(-x)与f(x)的关系;
3)作出相应结论:
若f(-x) = f(x) 或 f(-x)-f(x) = 0,则f(x)是偶函数;
若f(-x) =-f(x) 或 f(-x)+f(x) = 0,则f(x)是奇函数.
课堂练习
1.判断下列函数的奇偶性:
题型二、求函数解析式
例3、若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),求:当x≥0时,函数f(x)的解析式.
练习. 已知:函数
本课小结
1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
再 见
2.1.4函数的奇偶性
特点: 1.定义域关于原点对称;
2.图象关于原点对称;
3.对任意的x, f(-x)=-f(x).
课堂引入
x
0
y
y
x
0
●
●
-x
x
-x
x
●
●
设y=f(x)的定义域为D,对于函数定义域D内的任意一个x都有-x∈D,且
那么y=f(x)叫奇函数.
f(-x)=-f(x)
奇函数定义
奇函数的图象关于原点对称
特点:1.定义域关于原点对称;
2.图象关于y轴对称;
3.对任意的x, f(-x)=f(x).
课堂引入
-x
x
●
●
-x
x
●
●
偶函数定义
设y=f(x)的定义域为D,对于函数定义域D内的任意一个x都有-x∈D,且
那么y=f(x)叫偶函数.
f(-x)=f(x)
比较
奇函数
偶函数
(1)定义:
f(-x)= f(x)
(2)图像
f(-x)= - f(x)
奇函数的图象关于原点对称
偶函数的图象关于y轴对称
1、若函数f(x) 在区间[3-a,5]上是奇函数,则a的值是( )
思考
2、已知f(x) =x5+ax3+bx,若f(-2)=10,求f(2)=( )
0
y
x
y
x
⑴
⑵
小结: 图象法判断函数的奇偶性
练 习 判断下列函数的奇偶性
0
f(x)
g(x)
定义法判断函数的奇偶性:
3.利用定义判断函数奇偶性的格式步骤
1)首先确定函数的定义域,并判断其定义域是否关于原点对称;(如果定义域不关于原点对称,则函数非奇非偶,下面的步骤就不用)
2)确定f(-x)与f(x)的关系;
3)作出相应结论:
若f(-x) = f(x) 或 f(-x)-f(x) = 0,则f(x)是偶函数;
若f(-x) =-f(x) 或 f(-x)+f(x) = 0,则f(x)是奇函数.
课堂练习
1.判断下列函数的奇偶性:
题型二、求函数解析式
例3、若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),求:当x≥0时,函数f(x)的解析式.
练习. 已知:函数
本课小结
1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
再 见
