人教新课标高中数学B版必修1《3.1.2 指数函数》 课件(共27张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《3.1.2 指数函数》 课件(共27张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
1
0
x
y
问题1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数表达式是:
探究
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
8=23
第 x 次
……
表达式
一把长为1尺子第1次截去它的一半,第2次截去剩余部分的一半,第3次截去第2次剩余部分的一半, ······ ,依次截下去,问截的次数x与剩下的尺子长度y之间的关系:
问题2:半中折半
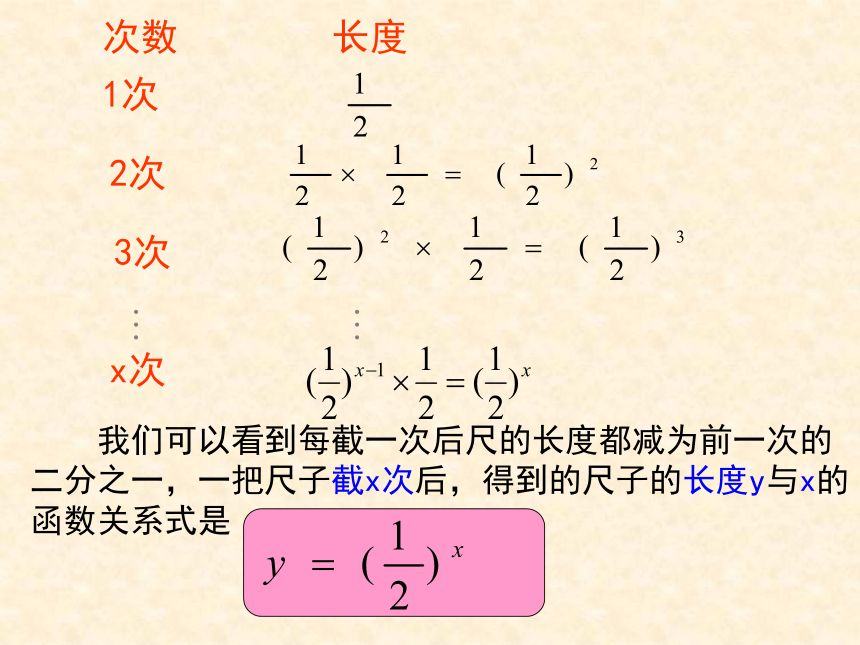
次数 长度
1次
2次
3次
…
…
我们可以看到每截一次后尺的长度都减为前一次的二分之一,一把尺子截x次后,得到的尺子的长度y与x的函数关系式是
x次
知识要点
指数函数定义:
形如y = ax ( a 0,且a 1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
在
,
中指数x是自变量,
底数是一个大于0且不等于1的常量.那我们能
概括怎样的数学模型?
讨论:为什么要规定a>0,且a≠1呢?
当a<0时,a x有些会没有意义,如
当a=0时, a x有些会没有意义,如
当a=1时,a x 恒等于1,没有研究的必要.
a 0,且 a 1.
(2)指数是 自变量
(1)底数a 0,且a 1;
定义特征
一、指数函数定义:
形如y = ax ( a 0,且a 1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
(3) 的系数为1
ax
小练习
判断下列函数哪些是指数函数?
不是
是
不是
不是
不是
是
在同一坐标系中分别作出如下函数的图像:
⑴列表 ⑵描点 ⑶连线
二、指数函数 图像和性质
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… 0.125 0.25 0.5 0.71 1 1.4 2 4 8 …
… 8 4 2 1.4 1 0.71 0.5 0.25 0.125 …
(2)描点 连线
返回
…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
8
4
2
1
0.5
0.25
0.13
…
y=2x
…
3
2
1
0
-1
-2
-3
…
x
(1) y=2x 与 y=3x的图象.
列表:
.
.
.
.
.
.
.
.
.
(0,1)
描点,连线
o
x
y
y=1
a>1
0图 象
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
过定 点:
( 0 , 1 )
x>0,y>1;
x<0, 0在 R 上是
增函数
x<0,y>1;
x>0,0在 R 上是
减函数
图象和性质:
y
1
0
x
y=ax(a>1)
a
1
y=( )x
1
0
x
y
y=
y=ax
(0x … -3 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 3 …
y=2x … 0.13 0.25 0.35 0.5 0.71 1 1.4 2 2.8 4 8 …
y=2-x … 8 4 2.8 2 1.4 1 0.71 0.5 0.35 0.25 0.13 …
=a-x
图象位置与底数关系
a-x
结论1:指数函数y=ax的图象与 的图象在同一坐标内关于y轴对称.
y=
a-x
图像
图像
x
o
y
结论2:
底数在第一象限按逆时针方向递增。
底数a
小
大
y=1x
例1:求下列函数的定义域与值域:
指数函数性质的应用
练一练
例2:比较下列各题中两个值的大小:
解:
⑴∵函数y=1.7x
在R上是增函数,
(1)1.72.5__ 1.73
(3)1.70.5__ 0.82.5
(2)0.8-1__0.8-2
∴1.72.5 < 1.73
又∵ 2.5 < 3 ,
指数函数性质的应用
⑵ ∵函数y=0.8x
在R上是减函数,
∴ 0.8—1 < 0.8 — 2
又∵ -1 > -2 ,
(2)0.8—1__0.8-2
∴1.70.5 > 0.82.5
∴ 1.7 0.5 > 1.70 = 1
∴ 0.8 2.5﹤ 0.80 =1,
(3)1.70.5__ 0.82.5
⑶∵函数y=1.7x
在R上是增函数,
∵函数y=0.8x
在R上是减函数,
(2)对不同底数,不同指数的幂的大小的比较可以用
中间量法:引进0或1或-1
如: 1.70.5>1.70 =1= 0.80 >0.82.5
(1)对同底数不同指数的幂大小的比较用的是构造函数法:利用指数函数的单调性如:
1.72.5 < 1.73
0.8—1 < 0.8 — 2
探究总结
课堂小结
1、指数函数概念
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
◆方法指导:
研究指数函数时,将a分为a>1和0a>1
0图 象
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
过定 点:
( 0 , 1 )
x>0,y>1;
x<0, 0在 R 上是
增函数
x<0,y>1;
x>0,0在 R 上是
减函数
2、指数函数 图像和性质
底数在第一象限按逆时针方向递增。
指数函数y=ax的图象与 的图象在同一坐标内关于y轴对称。
a
1
y=( )x
4.图像随底数的变化关系
3.对称性
④
③
y=1
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
①
②
1.如图是指数函数
①y=ax
④y=dx
③y=cx
②y=bx
(A)a﹤b﹤1﹤c﹤d
(B) b﹤a﹤1﹤d﹤c
(D) a﹤b﹤1﹤d﹤c
(C) 1﹤a﹤b﹤c﹤d
小结:利用图象随底数变化的关系----
底数在第一象限按逆时针方向递增
的图像,则a,b,c,d与1的大小关系是( )
B
X=1
底数a
小
大
作业:
Ⅰ 熟记指数函数的图象和性质
Ⅱ 导学P46
…
0.27
0.11
0.33
1
3
9
27
…
y=3-x
…
0.13
0.25
0.5
1
2
4
8
…
y=2-x
…
3
2
1
0
-1
-2
-3
…
x
(2)y=(1/2)x 与y=(1/3)x 的图象.
列表:
描点,连线
x
o
y
.
.
.
.
.
.
.
.
.
(0,1)
y=1
返回
1
0
x
y
问题1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数表达式是:
探究
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
8=23
第 x 次
……
表达式
一把长为1尺子第1次截去它的一半,第2次截去剩余部分的一半,第3次截去第2次剩余部分的一半, ······ ,依次截下去,问截的次数x与剩下的尺子长度y之间的关系:
问题2:半中折半
次数 长度
1次
2次
3次
…
…
我们可以看到每截一次后尺的长度都减为前一次的二分之一,一把尺子截x次后,得到的尺子的长度y与x的函数关系式是
x次
知识要点
指数函数定义:
形如y = ax ( a 0,且a 1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
在
,
中指数x是自变量,
底数是一个大于0且不等于1的常量.那我们能
概括怎样的数学模型?
讨论:为什么要规定a>0,且a≠1呢?
当a<0时,a x有些会没有意义,如
当a=0时, a x有些会没有意义,如
当a=1时,a x 恒等于1,没有研究的必要.
a 0,且 a 1.
(2)指数是 自变量
(1)底数a 0,且a 1;
定义特征
一、指数函数定义:
形如y = ax ( a 0,且a 1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
(3) 的系数为1
ax
小练习
判断下列函数哪些是指数函数?
不是
是
不是
不是
不是
是
在同一坐标系中分别作出如下函数的图像:
⑴列表 ⑵描点 ⑶连线
二、指数函数 图像和性质
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… 0.125 0.25 0.5 0.71 1 1.4 2 4 8 …
… 8 4 2 1.4 1 0.71 0.5 0.25 0.125 …
(2)描点 连线
返回
…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
8
4
2
1
0.5
0.25
0.13
…
y=2x
…
3
2
1
0
-1
-2
-3
…
x
(1) y=2x 与 y=3x的图象.
列表:
.
.
.
.
.
.
.
.
.
(0,1)
描点,连线
o
x
y
y=1
a>1
0
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0
定 义 域 :
R
值 域 :
( 0 , + ∞ )
过定 点:
( 0 , 1 )
x>0,y>1;
x<0, 0
增函数
x<0,y>1;
x>0,0
减函数
图象和性质:
y
1
0
x
y=ax(a>1)
a
1
y=( )x
1
0
x
y
y=
y=ax
(0
y=2x … 0.13 0.25 0.35 0.5 0.71 1 1.4 2 2.8 4 8 …
y=2-x … 8 4 2.8 2 1.4 1 0.71 0.5 0.35 0.25 0.13 …
=a-x
图象位置与底数关系
a-x
结论1:指数函数y=ax的图象与 的图象在同一坐标内关于y轴对称.
y=
a-x
图像
图像
x
o
y
结论2:
底数在第一象限按逆时针方向递增。
底数a
小
大
y=1x
例1:求下列函数的定义域与值域:
指数函数性质的应用
练一练
例2:比较下列各题中两个值的大小:
解:
⑴∵函数y=1.7x
在R上是增函数,
(1)1.72.5__ 1.73
(3)1.70.5__ 0.82.5
(2)0.8-1__0.8-2
∴1.72.5 < 1.73
又∵ 2.5 < 3 ,
指数函数性质的应用
⑵ ∵函数y=0.8x
在R上是减函数,
∴ 0.8—1 < 0.8 — 2
又∵ -1 > -2 ,
(2)0.8—1__0.8-2
∴1.70.5 > 0.82.5
∴ 1.7 0.5 > 1.70 = 1
∴ 0.8 2.5﹤ 0.80 =1,
(3)1.70.5__ 0.82.5
⑶∵函数y=1.7x
在R上是增函数,
∵函数y=0.8x
在R上是减函数,
(2)对不同底数,不同指数的幂的大小的比较可以用
中间量法:引进0或1或-1
如: 1.70.5>1.70 =1= 0.80 >0.82.5
(1)对同底数不同指数的幂大小的比较用的是构造函数法:利用指数函数的单调性如:
1.72.5 < 1.73
0.8—1 < 0.8 — 2
探究总结
课堂小结
1、指数函数概念
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
◆方法指导:
研究指数函数时,将a分为a>1和0
0
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0
定 义 域 :
R
值 域 :
( 0 , + ∞ )
过定 点:
( 0 , 1 )
x>0,y>1;
x<0, 0
增函数
x<0,y>1;
x>0,0
减函数
2、指数函数 图像和性质
底数在第一象限按逆时针方向递增。
指数函数y=ax的图象与 的图象在同一坐标内关于y轴对称。
a
1
y=( )x
4.图像随底数的变化关系
3.对称性
④
③
y=1
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
①
②
1.如图是指数函数
①y=ax
④y=dx
③y=cx
②y=bx
(A)a﹤b﹤1﹤c﹤d
(B) b﹤a﹤1﹤d﹤c
(D) a﹤b﹤1﹤d﹤c
(C) 1﹤a﹤b﹤c﹤d
小结:利用图象随底数变化的关系----
底数在第一象限按逆时针方向递增
的图像,则a,b,c,d与1的大小关系是( )
B
X=1
底数a
小
大
作业:
Ⅰ 熟记指数函数的图象和性质
Ⅱ 导学P46
…
0.27
0.11
0.33
1
3
9
27
…
y=3-x
…
0.13
0.25
0.5
1
2
4
8
…
y=2-x
…
3
2
1
0
-1
-2
-3
…
x
(2)y=(1/2)x 与y=(1/3)x 的图象.
列表:
描点,连线
x
o
y
.
.
.
.
.
.
.
.
.
(0,1)
y=1
返回
