人教新课标高中数学B版必修1《1.2.2 集合的运算》 课件(共22张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《1.2.2 集合的运算》 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 599.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
集合的运算
A
B
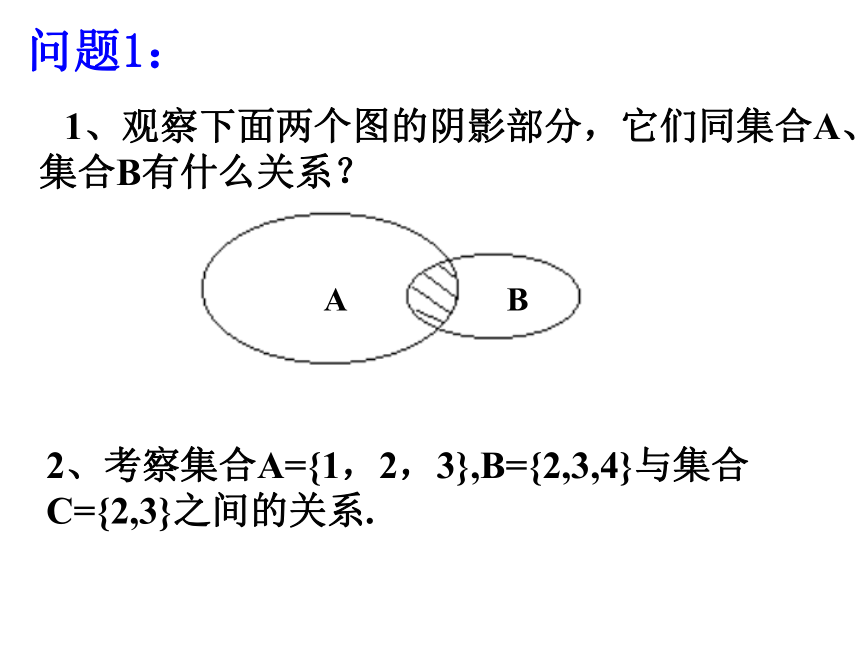
1、观察下面两个图的阴影部分,它们同集合A、集合B有什么关系?
2、考察集合A={1,2,3},B={2,3,4}与集合C={2,3}之间的关系.
问题1:
一、交集
6的正约数集A
6 与8的正公约数集是{ 1,2}
8的正约数集B
定义:一般地,对于两个给定的集合A、B,由属于A又属于B的所有元素构成的集合,称为A与B的交集
记作 A∩B={ x| x∈A且x∈B }
A∩B的元素实质是A与B的公共元素
A∩B读作“A交B”
={ 3,6}
={ 4,8 }
1,2,
1,2,
已知集合A={a,b,c} B={c,d,e,f} C={a,b,c,d,e}
求①A∩B ②B∩A ③A∩
④A∩C
问题2:
①A∩B={c}
②B∩A ={c}
③A∩ =
④A∩C={a,b,c}
A∩A=A
A∩B=B∩A
A∩Φ=Φ∩A =Φ
A B A∩B=A
结论:对于任意两个集合A、B,都有:
A
B
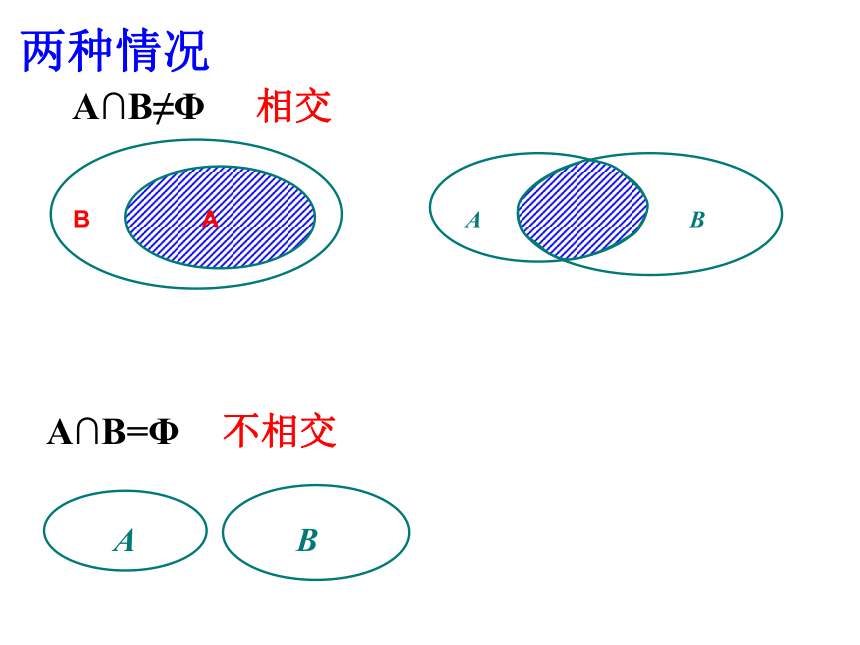
A∩B≠Φ
A∩B=Φ
相交
不相交
B
A
A
B
两种情况
例1.A={-4,-3,-2,-1,0,1,2}
B={4,3,2,1,0,-1,-2},
求A∩B
例题:
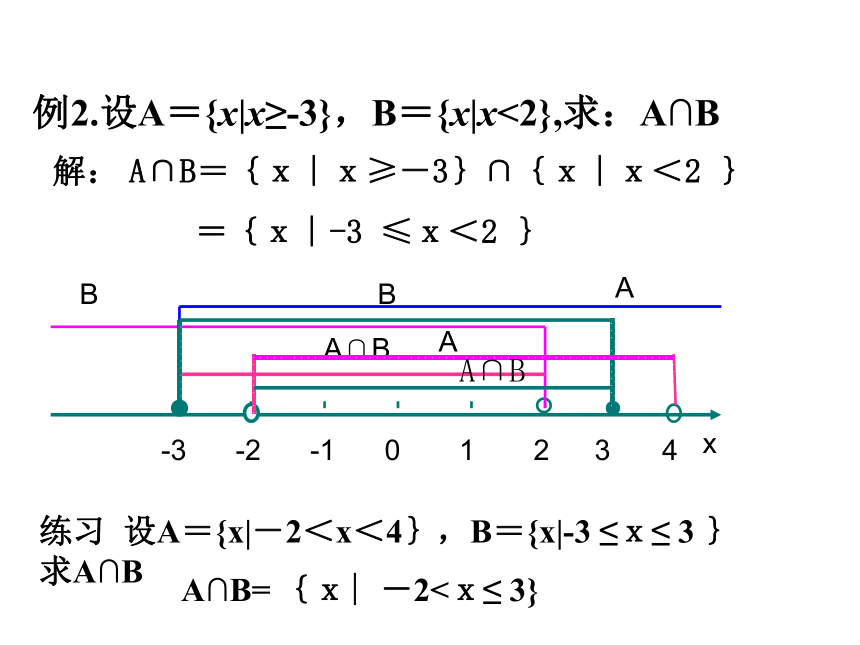
例2.设A={x|x≥-3},B={x|x<2},求:A∩B
解: A∩B={x∣x≥-3}∩{x∣x<2 }
={x∣-3 ≤x<2 }
-3
-2
-1
0
1
2
A
B
A∩B
x
练习 设A={x|-2<x<4},B={x|-3 ≤x≤ 3 }
求A∩B
3
4
B
A
A∩B
A∩B= {x∣-2<x≤ 3}
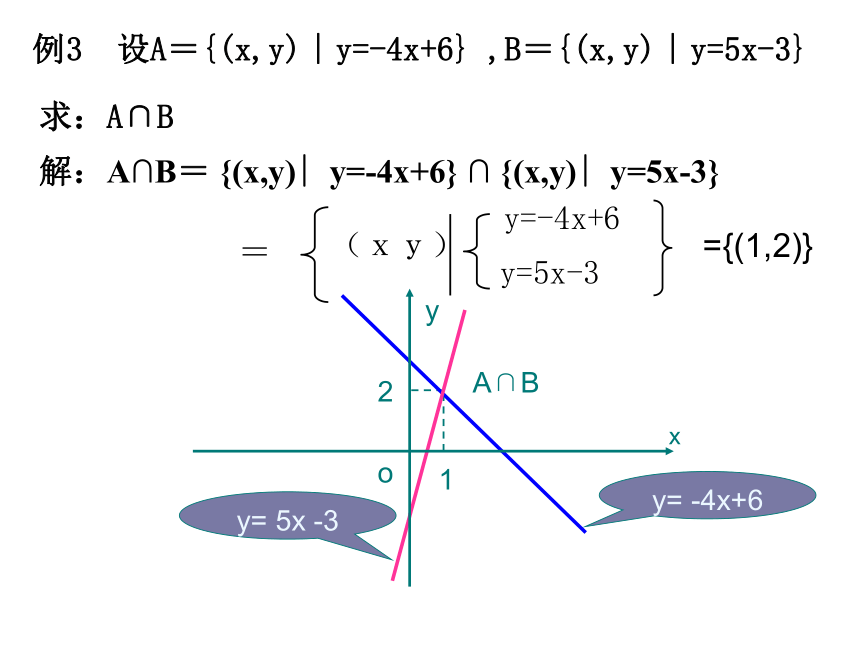
例3 设A={(x,y)∣y=-4x+6} ,B={(x,y)∣y=5x-3}
求:A∩B
解:A∩B= {(x,y)∣y=-4x+6} ∩ {(x,y)∣y=5x-3}
y=-4x+6
y=5x-3
(xy)
=
={(1,2)}
A∩B
2
1
y= -4x+6
y= 5x -3
o
y
x
A
B
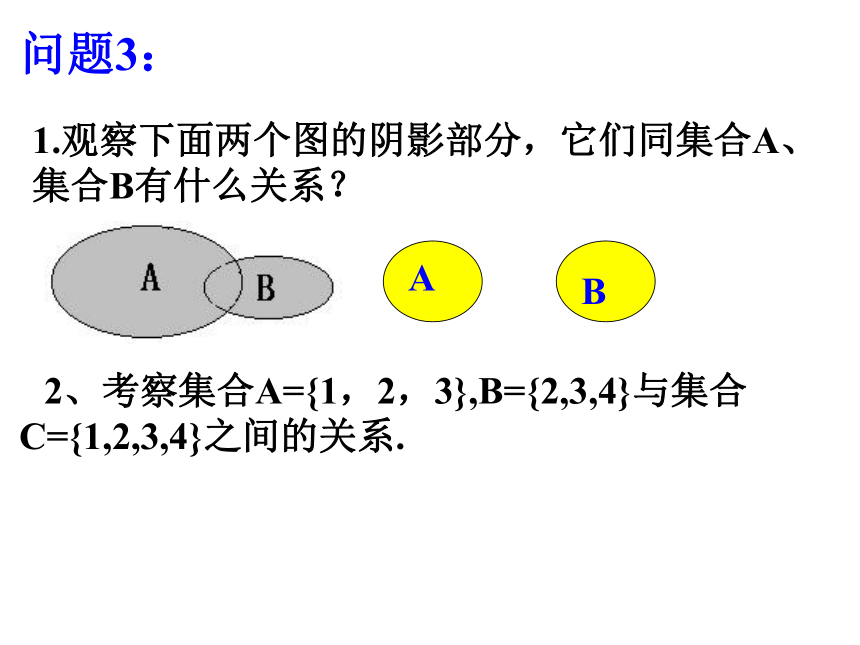
1.观察下面两个图的阴影部分,它们同集合A、集合B有什么关系?
2、考察集合A={1,2,3},B={2,3,4}与集合C={1,2,3,4}之间的关系.
问题3:
二、并集
方程x2-1=0的解集A={ 1,-1}
记作 A∪B={ x| x∈A或x∈B }
A∪B读作“A并B”
方程x2-4=0的解集B={ 2,-2 }
方程(x2-1)(x2-4)=0的解集是{-1,1,2,-2}
定义:一般地,对于两个给定的集合A、B,由两个集合的所有元素构成的集合,叫做A与B的并集
A∪B的元素实质是A与B的一切元素
A∪B
A∪B(元素相加)
相交
不相交
A
B
B
A
B
A
A∪B=B
A∪A=A
A∪B=B∪A
A∪Φ=A∪Φ=A
A B
例4 设A={ -2,-1,0,1,2 } ,B={ 1,2,3,4,5 },
求A∪B。
解: A∪B={-2,-1,0,1,2}∪{1,2,3,4,5}
={-2,-1, 0,1,2,3,4,5}
练习:A={-4,-3,-2,-1,0,1,2}
B={4,,3,2,1,0,-1,-2},
C={-4,-3,-2,-1,0,1,5}
求A∪B ,B ∪C
例5 设A={x|-2解:A∪B= {x|-2-2
-1
0
1
2
3
4
5
A∪B
A
B
x
= {x|-2<x≤ 5}
练习:设A={x|-2-3
A
B
A∪B
A∪B= {x∣-3≤x< 4}
例6 设A={x|x≤-3},B={x|x>2},求:A∪B
解: A∪B={x|x≤-3}∪{x|x>2}
={x|x≤-3或x>2}
-3
-2
-1
0
1
2
A
B
x
练习:设A为奇数集,B为偶数集,Z为整数集,求A∩Z,A∩B,B∩Z,A∪B,A∪Z,B∪Z。
问题4
集合U={1,2,3,4,5,6,7},集合A={2,5,7},B={1,3,4,6},
A∪B=U,那么A,B,U之间还有什么关系呢?
方程x2-1=0的解集A={ 1,-1}
方程x2-4=0的解集B={ 2,-2 }
方程(x2-1)(x2-4)=0的解集是{-1,1,2,-2}
三、补集
1.全集:如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示
2.补集:如果给定集合A是全集U的一个子集,由U中不属于A的所有元素构成的集合,叫做A在U中的补集,记做:
CUA即:CUA={x|x∈U且x A}
读作:A在U中的补集
说明:补集的概念必须要有全集的限制
3.补集的性质
1、分别用集合A,B,C表示下图的阴影部分
练习:
,
2、已知全集I=
,若
,求实数
3、已知全集
,集合
,
,其中
,若
,求
4、已知全集I={小于10的正整数},其子集A,B满足
,
,
求集合A,B
小结
定义:设A、B是两个集合,由属于A或属于B的所有元素组成的集合,称为A与B的并集
记作 A∪B={ x| x∈A或x∈B }
定义:设A、B是两个集合,由属于A又属于B的所有元素组成的集合,称为A与B的交集
记作 A∩B={ x| x∈A又x∈B }
A∪B的元素实质是A与B的一切元素
由两个集合A与B运算出一个新的集合,涉及到三个集合。
A∩B的元素实质是A与B的公共元素
相同点:
不同点:
三、补集
1.全集:如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示
2.补集:如果给定集合A是全集U的一个子集,由U中不属于A的所有元素构成的集合,叫做A在U中的补集,记做:
CUA即:CUA={x|x∈U且x A}
读作:A在U中的补集
说明:补集的概念必须要有全集的限制
练习:
19 页练习A, 练习B
作业:
1.课本 20 页习题1-2A 第3、9题
2.复习本章内容
集合的运算
A
B
1、观察下面两个图的阴影部分,它们同集合A、集合B有什么关系?
2、考察集合A={1,2,3},B={2,3,4}与集合C={2,3}之间的关系.
问题1:
一、交集
6的正约数集A
6 与8的正公约数集是{ 1,2}
8的正约数集B
定义:一般地,对于两个给定的集合A、B,由属于A又属于B的所有元素构成的集合,称为A与B的交集
记作 A∩B={ x| x∈A且x∈B }
A∩B的元素实质是A与B的公共元素
A∩B读作“A交B”
={ 3,6}
={ 4,8 }
1,2,
1,2,
已知集合A={a,b,c} B={c,d,e,f} C={a,b,c,d,e}
求①A∩B ②B∩A ③A∩
④A∩C
问题2:
①A∩B={c}
②B∩A ={c}
③A∩ =
④A∩C={a,b,c}
A∩A=A
A∩B=B∩A
A∩Φ=Φ∩A =Φ
A B A∩B=A
结论:对于任意两个集合A、B,都有:
A
B
A∩B≠Φ
A∩B=Φ
相交
不相交
B
A
A
B
两种情况
例1.A={-4,-3,-2,-1,0,1,2}
B={4,3,2,1,0,-1,-2},
求A∩B
例题:
例2.设A={x|x≥-3},B={x|x<2},求:A∩B
解: A∩B={x∣x≥-3}∩{x∣x<2 }
={x∣-3 ≤x<2 }
-3
-2
-1
0
1
2
A
B
A∩B
x
练习 设A={x|-2<x<4},B={x|-3 ≤x≤ 3 }
求A∩B
3
4
B
A
A∩B
A∩B= {x∣-2<x≤ 3}
例3 设A={(x,y)∣y=-4x+6} ,B={(x,y)∣y=5x-3}
求:A∩B
解:A∩B= {(x,y)∣y=-4x+6} ∩ {(x,y)∣y=5x-3}
y=-4x+6
y=5x-3
(xy)
=
={(1,2)}
A∩B
2
1
y= -4x+6
y= 5x -3
o
y
x
A
B
1.观察下面两个图的阴影部分,它们同集合A、集合B有什么关系?
2、考察集合A={1,2,3},B={2,3,4}与集合C={1,2,3,4}之间的关系.
问题3:
二、并集
方程x2-1=0的解集A={ 1,-1}
记作 A∪B={ x| x∈A或x∈B }
A∪B读作“A并B”
方程x2-4=0的解集B={ 2,-2 }
方程(x2-1)(x2-4)=0的解集是{-1,1,2,-2}
定义:一般地,对于两个给定的集合A、B,由两个集合的所有元素构成的集合,叫做A与B的并集
A∪B的元素实质是A与B的一切元素
A∪B
A∪B(元素相加)
相交
不相交
A
B
B
A
B
A
A∪B=B
A∪A=A
A∪B=B∪A
A∪Φ=A∪Φ=A
A B
例4 设A={ -2,-1,0,1,2 } ,B={ 1,2,3,4,5 },
求A∪B。
解: A∪B={-2,-1,0,1,2}∪{1,2,3,4,5}
={-2,-1, 0,1,2,3,4,5}
练习:A={-4,-3,-2,-1,0,1,2}
B={4,,3,2,1,0,-1,-2},
C={-4,-3,-2,-1,0,1,5}
求A∪B ,B ∪C
例5 设A={x|-2
-1
0
1
2
3
4
5
A∪B
A
B
x
= {x|-2<x≤ 5}
练习:设A={x|-2
A
B
A∪B
A∪B= {x∣-3≤x< 4}
例6 设A={x|x≤-3},B={x|x>2},求:A∪B
解: A∪B={x|x≤-3}∪{x|x>2}
={x|x≤-3或x>2}
-3
-2
-1
0
1
2
A
B
x
练习:设A为奇数集,B为偶数集,Z为整数集,求A∩Z,A∩B,B∩Z,A∪B,A∪Z,B∪Z。
问题4
集合U={1,2,3,4,5,6,7},集合A={2,5,7},B={1,3,4,6},
A∪B=U,那么A,B,U之间还有什么关系呢?
方程x2-1=0的解集A={ 1,-1}
方程x2-4=0的解集B={ 2,-2 }
方程(x2-1)(x2-4)=0的解集是{-1,1,2,-2}
三、补集
1.全集:如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示
2.补集:如果给定集合A是全集U的一个子集,由U中不属于A的所有元素构成的集合,叫做A在U中的补集,记做:
CUA即:CUA={x|x∈U且x A}
读作:A在U中的补集
说明:补集的概念必须要有全集的限制
3.补集的性质
1、分别用集合A,B,C表示下图的阴影部分
练习:
,
2、已知全集I=
,若
,求实数
3、已知全集
,集合
,
,其中
,若
,求
4、已知全集I={小于10的正整数},其子集A,B满足
,
,
求集合A,B
小结
定义:设A、B是两个集合,由属于A或属于B的所有元素组成的集合,称为A与B的并集
记作 A∪B={ x| x∈A或x∈B }
定义:设A、B是两个集合,由属于A又属于B的所有元素组成的集合,称为A与B的交集
记作 A∩B={ x| x∈A又x∈B }
A∪B的元素实质是A与B的一切元素
由两个集合A与B运算出一个新的集合,涉及到三个集合。
A∩B的元素实质是A与B的公共元素
相同点:
不同点:
三、补集
1.全集:如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示
2.补集:如果给定集合A是全集U的一个子集,由U中不属于A的所有元素构成的集合,叫做A在U中的补集,记做:
CUA即:CUA={x|x∈U且x A}
读作:A在U中的补集
说明:补集的概念必须要有全集的限制
练习:
19 页练习A, 练习B
作业:
1.课本 20 页习题1-2A 第3、9题
2.复习本章内容
