人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》 课件(共24张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
2.1.4 函数的奇偶性
从对称角度思考下列各图有什么特点?
引入新课
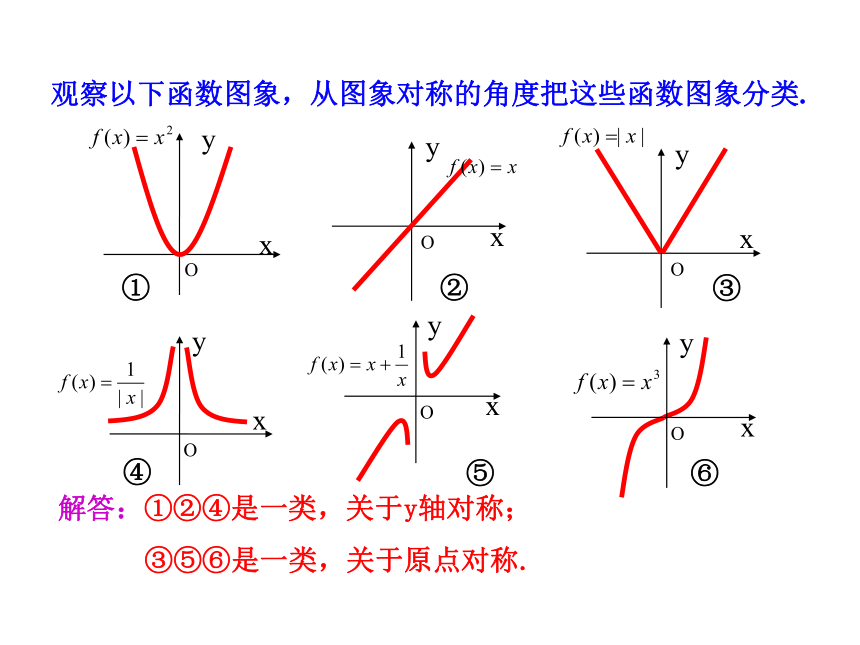
观察以下函数图象,从图象对称的角度把这些函数图象分类.
y
O
x
①
O
x
y
②
③
O
x
y
O
x
y
④
⑤
O
x
y
O
x
y
⑥
解答:①②④是一类,关于y轴对称;
③⑤⑥是一类,关于原点对称.
思考1、请观察以下各点与点(X,Y)之间有什么对称
关系?
y
O
-2
f(x)=x2
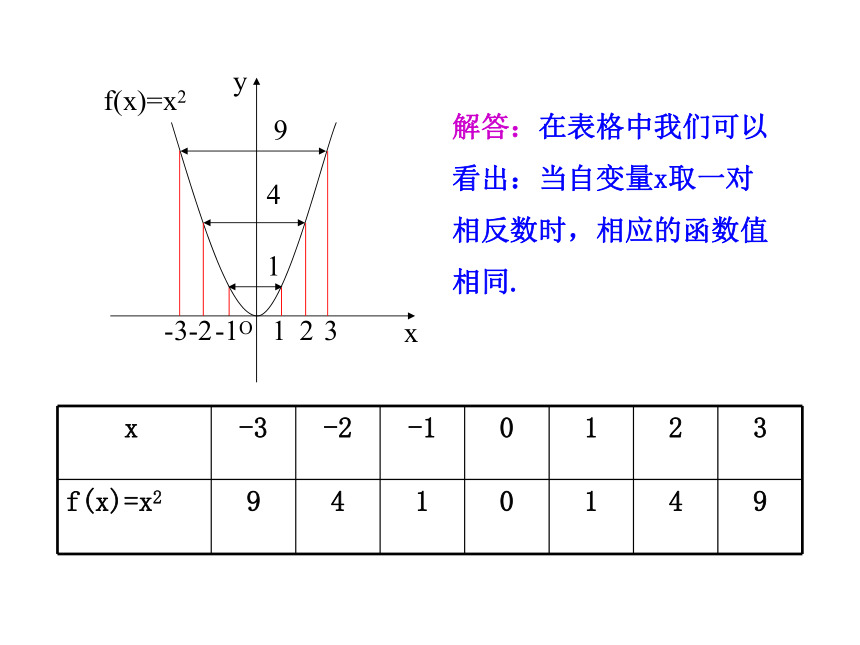
解答:在表格中我们可以看出:当自变量x取一对相反数时,相应的函数值相同.
x -3 -2 -1 0 1 2 3
f(x)=x2 9 4 1 0 1 4 9
x
9
4
1
-3
3
1
-1
2
P/(-x,f(-x))
P/(-x,f(x))
O
x
x
-x
y
P(x,f(x))
f(-x)=f(x)
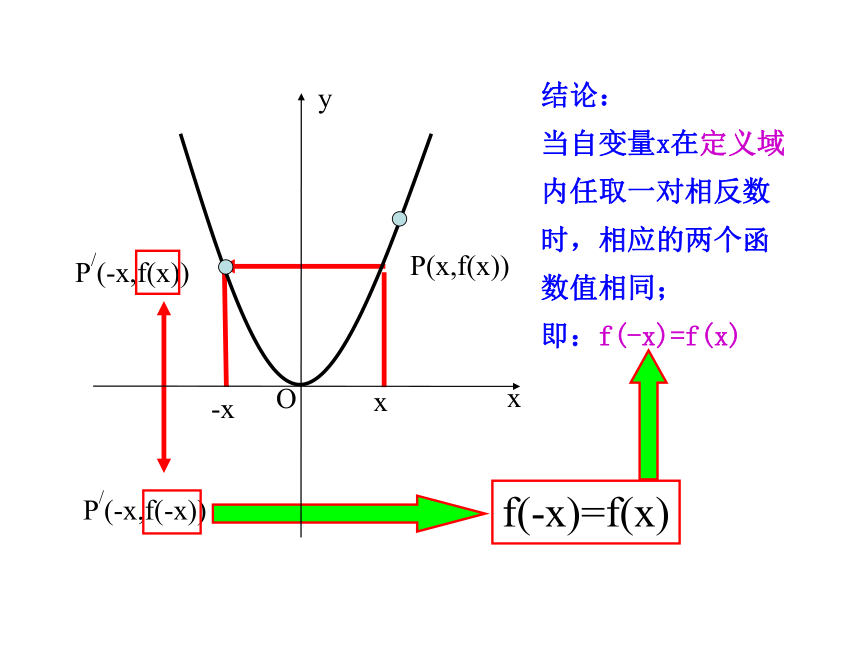
结论:
当自变量x在定义域内任取一对相反数时,相应的两个函数值相同;
即:f(-x)=f(x)
思考2:一般地,若函数y=f(x)的图象关于y轴对称,则f(x)与f(-x)有什么关系?反之成立吗?
解答:f(x)=f(-x),反之也成立。
思考3:我们把具有上述特征的函数叫做偶函数,那么怎样定义偶函数?
设函数y=f(x)的定义域为D,如果对D内的任意一个x,都有-x D,且f(-x)=f(x) ,则这个函数叫做偶函数.
思考4:观察下面的函数图象,判断函数是不是偶函数.
思考5:如果一个函数的图象关于y轴对称,那么它的定义域应该有什么特点?
解答:
定义域应该关于原点对称.
O
x
y
解答:图象关于y轴对称,是偶函数。
说明
1.偶函数指的是函数的整体性质,是对整个定义域而言的.
2.函数是偶函数的前提条件是定义域关于原点对称.
要注意关于原点对称的含义.
3.在前提条件下,
偶函数 f(x)=f(-x) f(x)-f(-x)=0
图象关于y轴对称.
思考6:继续观察下面的3幅函数图象:
O
x
y
②
O
x
y
⑥
⑤
O
x
y
根据我们由图象推导偶函数的方法和步骤,同学们结合课本内容归纳一下奇函数的定义.
由此我们可以得到奇函数的定义:
设函数y=f(x)的定义域为D,如果对D内的任意一个x, 都有-x D ,且________________,则这个函数叫做奇函数.
f(-x)= -f(x)
思考7:如果一个函数的图象关于原点对称,那么它的定义域应该有什么特点?
解答:定义域也应该关于原点对称!
想一想
解答:判断或证明函数奇偶性的基本步骤:
思考8:如何根据定义判断下列函数的奇偶性
1、奇函数的图象关于原点对称.
反过来,如果一个函数的图象关于原点对称,则这个函数为奇函数.
2、偶函数的图象关于y轴对称.
反过来,如果一个函数的图象关于y轴对称,则这个函数为偶函数.
说明:奇偶函数图象的性质可用于:
a、简化函数图象的画法.
b、判断函数的奇偶性
奇偶函数图象的性质
已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.
x
y
0
相等
例1、判断下列函数的奇偶性.
(3)
解:(1) 因为f(-x)=2x= -f(x) ,所以f(x)是奇函数.
因为 f(-x)=|-x|-2=|x|-2=f(x) ,所以f(x)是偶函数.
因为
是偶函数.
(1)
(2)
判断奇偶性,只需验证f(x)与f(-x)之间的关系。
(5)
(6)
(4)
定义域关于原 点对称是函数具有奇偶性的前提条件。
解:(4)当x=2时,由于2 [-3,1],故f(2)不存在,所以就谈不上与f(-2)相等了,由于任意性受破坏。所以它没有奇偶性.
(5)函数的定义域为[-2,2),故f(2)不存在,同上可知函数没有奇偶性.
(6)因为f(-x)= -2x-1,∴f( -x )≠ f( x )且f( -x )≠ -f( x ),故函数没有奇偶性.
(1)f(x)=x +2x; (2) f(x)=2x +3x ;
3
2
4
(3) f(x)=√x-1 +√1-x ; (4) f(x)= √x2 -1 +√1-x2,
(5) f(x)=︱x︱(x +1); (6) f(x)= √x + .
1
x
2
练习1:判断下列函数的奇偶性.
奇函数
既是奇函数又是偶函数
既是奇函数又是偶函数
既非奇函数又非偶函数
既非奇函数又非偶函数
偶函数
例2、已知函数f(x)既是奇函数又是偶函数。
求证:f(x)=0.
证明:因为 f(x)既是奇函数又是偶函数,
所以 f(-x)=f(x),且f(-x)= -f(x),
所以 f(x)= -f(x),
所以 2f(x)=0,
即 f(x)=0.
这样的函数有多少个呢?
若函数 为奇函数,求c的值.
练习2
解:由f(-x)= -f(x)可得c=0.
1.两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数;
如果都有f(-x)=f(x) f(x)为偶函数.
2.两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
3.(1)理解奇、偶函数的概念及图象特征.
(2)能判断函数的奇偶性.
看似平坦的成功之路往往是由无数失败的石头加之努力的柏油铺成的。
2.1.4 函数的奇偶性
从对称角度思考下列各图有什么特点?
引入新课
观察以下函数图象,从图象对称的角度把这些函数图象分类.
y
O
x
①
O
x
y
②
③
O
x
y
O
x
y
④
⑤
O
x
y
O
x
y
⑥
解答:①②④是一类,关于y轴对称;
③⑤⑥是一类,关于原点对称.
思考1、请观察以下各点与点(X,Y)之间有什么对称
关系?
y
O
-2
f(x)=x2
解答:在表格中我们可以看出:当自变量x取一对相反数时,相应的函数值相同.
x -3 -2 -1 0 1 2 3
f(x)=x2 9 4 1 0 1 4 9
x
9
4
1
-3
3
1
-1
2
P/(-x,f(-x))
P/(-x,f(x))
O
x
x
-x
y
P(x,f(x))
f(-x)=f(x)
结论:
当自变量x在定义域内任取一对相反数时,相应的两个函数值相同;
即:f(-x)=f(x)
思考2:一般地,若函数y=f(x)的图象关于y轴对称,则f(x)与f(-x)有什么关系?反之成立吗?
解答:f(x)=f(-x),反之也成立。
思考3:我们把具有上述特征的函数叫做偶函数,那么怎样定义偶函数?
设函数y=f(x)的定义域为D,如果对D内的任意一个x,都有-x D,且f(-x)=f(x) ,则这个函数叫做偶函数.
思考4:观察下面的函数图象,判断函数是不是偶函数.
思考5:如果一个函数的图象关于y轴对称,那么它的定义域应该有什么特点?
解答:
定义域应该关于原点对称.
O
x
y
解答:图象关于y轴对称,是偶函数。
说明
1.偶函数指的是函数的整体性质,是对整个定义域而言的.
2.函数是偶函数的前提条件是定义域关于原点对称.
要注意关于原点对称的含义.
3.在前提条件下,
偶函数 f(x)=f(-x) f(x)-f(-x)=0
图象关于y轴对称.
思考6:继续观察下面的3幅函数图象:
O
x
y
②
O
x
y
⑥
⑤
O
x
y
根据我们由图象推导偶函数的方法和步骤,同学们结合课本内容归纳一下奇函数的定义.
由此我们可以得到奇函数的定义:
设函数y=f(x)的定义域为D,如果对D内的任意一个x, 都有-x D ,且________________,则这个函数叫做奇函数.
f(-x)= -f(x)
思考7:如果一个函数的图象关于原点对称,那么它的定义域应该有什么特点?
解答:定义域也应该关于原点对称!
想一想
解答:判断或证明函数奇偶性的基本步骤:
思考8:如何根据定义判断下列函数的奇偶性
1、奇函数的图象关于原点对称.
反过来,如果一个函数的图象关于原点对称,则这个函数为奇函数.
2、偶函数的图象关于y轴对称.
反过来,如果一个函数的图象关于y轴对称,则这个函数为偶函数.
说明:奇偶函数图象的性质可用于:
a、简化函数图象的画法.
b、判断函数的奇偶性
奇偶函数图象的性质
已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.
x
y
0
相等
例1、判断下列函数的奇偶性.
(3)
解:(1) 因为f(-x)=2x= -f(x) ,所以f(x)是奇函数.
因为 f(-x)=|-x|-2=|x|-2=f(x) ,所以f(x)是偶函数.
因为
是偶函数.
(1)
(2)
判断奇偶性,只需验证f(x)与f(-x)之间的关系。
(5)
(6)
(4)
定义域关于原 点对称是函数具有奇偶性的前提条件。
解:(4)当x=2时,由于2 [-3,1],故f(2)不存在,所以就谈不上与f(-2)相等了,由于任意性受破坏。所以它没有奇偶性.
(5)函数的定义域为[-2,2),故f(2)不存在,同上可知函数没有奇偶性.
(6)因为f(-x)= -2x-1,∴f( -x )≠ f( x )且f( -x )≠ -f( x ),故函数没有奇偶性.
(1)f(x)=x +2x; (2) f(x)=2x +3x ;
3
2
4
(3) f(x)=√x-1 +√1-x ; (4) f(x)= √x2 -1 +√1-x2,
(5) f(x)=︱x︱(x +1); (6) f(x)= √x + .
1
x
2
练习1:判断下列函数的奇偶性.
奇函数
既是奇函数又是偶函数
既是奇函数又是偶函数
既非奇函数又非偶函数
既非奇函数又非偶函数
偶函数
例2、已知函数f(x)既是奇函数又是偶函数。
求证:f(x)=0.
证明:因为 f(x)既是奇函数又是偶函数,
所以 f(-x)=f(x),且f(-x)= -f(x),
所以 f(x)= -f(x),
所以 2f(x)=0,
即 f(x)=0.
这样的函数有多少个呢?
若函数 为奇函数,求c的值.
练习2
解:由f(-x)= -f(x)可得c=0.
1.两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数;
如果都有f(-x)=f(x) f(x)为偶函数.
2.两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
3.(1)理解奇、偶函数的概念及图象特征.
(2)能判断函数的奇偶性.
看似平坦的成功之路往往是由无数失败的石头加之努力的柏油铺成的。
