人教新课标高中数学B版必修1《3.3 幂函数》 课件(共26张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《3.3 幂函数》 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 16:16:15 | ||
图片预览






文档简介
(共26张PPT)
数学
路漫漫其修远兮 吾将上下而求索
人教B版 · 必修1
3.3 幂函数
第三章
课堂自主探究
2
例题讲解
3
课 时 作 业
4
复习导入
1
复习导入
回忆:什么是指数函数?
思考:函数y=x,y=x2,y=x3,y=x-1 这些是指数函数吗?
以上几个函数的解析式有什么共同特征
1.一般地形如______________的函数叫做幂函数.
结构特征:幂值前系数为1,底数是自变量x,指数是常数.
思考:幂函数与指数函数的联系?
y=xα(α为常数)
判断:下列函数是否为幂函数
这四个都不是,不满足幂函数的结构特征
学生活动一:
在同一坐标系中,画出这五个常见的幂函数图象。
课堂自主探究
1
2
-1
-2
1
2
-1
-2
1
1
2
3
1
-1
x
y
x
y
1 2
-2 -1
-1
-2
2
1
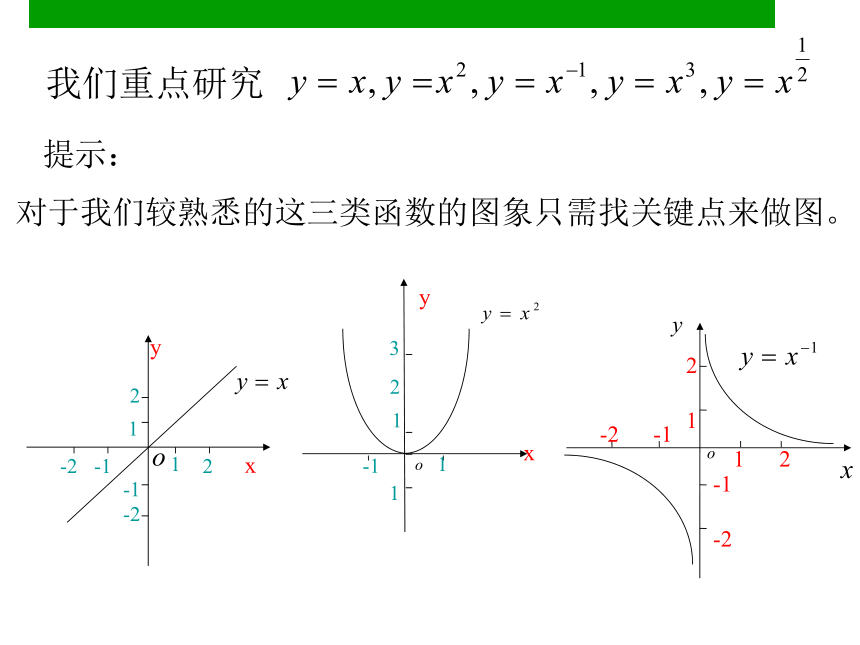
我们重点研究
提示:
对于我们较熟悉的这三类函数的图象只需找关键点来做图。
o
o
1
1
2
-1
-2
1
1
-1
-1
-2
-2
-1
2
3
4
6
1
0
1
2
0
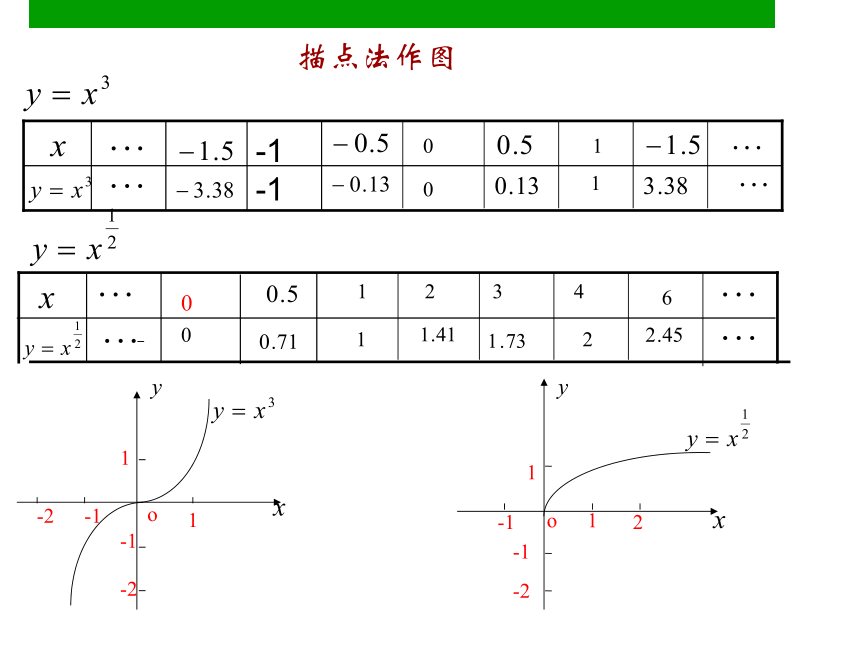
描点法作图
-1
-1
0
1
0
1
列表如下:
R
奇
增函数
[0,+∞)
减函数
奇
增函数
[0,+∞)
增函数
(-∞,0)∪
(0,+∞)
奇
减函数
学生活动二:
以小组为单位,结合表格,讨论幂函数的性质.
思考:(随着 值不同性质也不相同)
(1)幂函数的图象可能在第四象限吗?
哪个象限可能有幂函数的图象?
(2)恒过哪个定点?为什么?
(3)当 取不同范围时(在第一象限中),图象有什么不同?单调性有什么不同?
(4)若能确定第一象限的图象就能确定整个定义域的图象吗?为什么?
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1, 1);
(2) 如果α>0,则幂函数图象通过(0,0),并且在区间[0,+∞)上是增函数;
(3) 如果α<0,则幂函数在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,当x趋于+∞时,图象在x轴上方无限逼近x轴。
幂函数的性质
【例1】 函数f(x)=(m2-m-5)xm-1是幂函数,且当x∈(0,+∞)时,f(x)是增函数,试确定m的值.
.
分析:由已知f(x)=(m2-m-5)·xm-1是幂函数,且当x>0时是增函数,可先利用幂函数的定义求出m的值,再利用单调性确定m的值.
解:根据幂函数的定义,得m2-m-5=1,
解得m=3或m=-2.
当m=3时,f(x)=x2在(0,+∞)上是增函数;
当m=-2时,f(x)=x-3在(0,+∞)上是减函数,不符合要求.故m=3.
例题讲解
幂函数的性质
【例2】比较下列两个代数值的大小
比较代数式大小的方法总结:
同底的幂,用指数函数单调性;
同指数的幂,用幂函数 单调性;
底数与指数均不相同的幂,通常是找一中间值过渡或化同底(化同指)
【例3】求下列幂函数的定义域,并指出其奇偶性、单调性.
课堂检测
(点此链接)
[思路分析] (1)当给定的两个幂的幂指数相同时,如何比较它们的大小?
(2)如果两个幂的底数和指数都不同,那么如何比较它们的大小?
[规律总结] 1.注意利用幂函数的性质比较幂值大小的方法步骤.
第一步,据指数分清正负;
第二步,正数区分大于1与小于1的,a>1,α>0时,aα>1;00时01,α<0时01;
第三步,构造幂函数应用幂函数单调性,特别注意含字母时,要注意底数不在同一单调区间内的情形.
2.给定一组数值,比较大小的步骤.
第一步:区分正负.一种情形是幂函数或指数函数值即幂式确定符号;另一种情形是对数式确定符号,要根据各自的性质进行.
第二步:正数通常还要区分大于1还是小于1.
第三步:同底的幂,用指数函数单调性;同指数的幂用幂函数单调性;同底的对数用对数函数单调性.
第四步:对于底数与指数均不相同的幂,或底数与真数均不相同的对数值大小的比较,通常是找一中间值过渡或化同底(化同指)、或放缩、有时作商(或作差)、或指对互化,对数式有时还用换底公式作变换等等.
数学
路漫漫其修远兮 吾将上下而求索
人教B版 · 必修1
3.3 幂函数
第三章
课堂自主探究
2
例题讲解
3
课 时 作 业
4
复习导入
1
复习导入
回忆:什么是指数函数?
思考:函数y=x,y=x2,y=x3,y=x-1 这些是指数函数吗?
以上几个函数的解析式有什么共同特征
1.一般地形如______________的函数叫做幂函数.
结构特征:幂值前系数为1,底数是自变量x,指数是常数.
思考:幂函数与指数函数的联系?
y=xα(α为常数)
判断:下列函数是否为幂函数
这四个都不是,不满足幂函数的结构特征
学生活动一:
在同一坐标系中,画出这五个常见的幂函数图象。
课堂自主探究
1
2
-1
-2
1
2
-1
-2
1
1
2
3
1
-1
x
y
x
y
1 2
-2 -1
-1
-2
2
1
我们重点研究
提示:
对于我们较熟悉的这三类函数的图象只需找关键点来做图。
o
o
1
1
2
-1
-2
1
1
-1
-1
-2
-2
-1
2
3
4
6
1
0
1
2
0
描点法作图
-1
-1
0
1
0
1
列表如下:
R
奇
增函数
[0,+∞)
减函数
奇
增函数
[0,+∞)
增函数
(-∞,0)∪
(0,+∞)
奇
减函数
学生活动二:
以小组为单位,结合表格,讨论幂函数的性质.
思考:(随着 值不同性质也不相同)
(1)幂函数的图象可能在第四象限吗?
哪个象限可能有幂函数的图象?
(2)恒过哪个定点?为什么?
(3)当 取不同范围时(在第一象限中),图象有什么不同?单调性有什么不同?
(4)若能确定第一象限的图象就能确定整个定义域的图象吗?为什么?
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1, 1);
(2) 如果α>0,则幂函数图象通过(0,0),并且在区间[0,+∞)上是增函数;
(3) 如果α<0,则幂函数在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,当x趋于+∞时,图象在x轴上方无限逼近x轴。
幂函数的性质
【例1】 函数f(x)=(m2-m-5)xm-1是幂函数,且当x∈(0,+∞)时,f(x)是增函数,试确定m的值.
.
分析:由已知f(x)=(m2-m-5)·xm-1是幂函数,且当x>0时是增函数,可先利用幂函数的定义求出m的值,再利用单调性确定m的值.
解:根据幂函数的定义,得m2-m-5=1,
解得m=3或m=-2.
当m=3时,f(x)=x2在(0,+∞)上是增函数;
当m=-2时,f(x)=x-3在(0,+∞)上是减函数,不符合要求.故m=3.
例题讲解
幂函数的性质
【例2】比较下列两个代数值的大小
比较代数式大小的方法总结:
同底的幂,用指数函数单调性;
同指数的幂,用幂函数 单调性;
底数与指数均不相同的幂,通常是找一中间值过渡或化同底(化同指)
【例3】求下列幂函数的定义域,并指出其奇偶性、单调性.
课堂检测
(点此链接)
[思路分析] (1)当给定的两个幂的幂指数相同时,如何比较它们的大小?
(2)如果两个幂的底数和指数都不同,那么如何比较它们的大小?
[规律总结] 1.注意利用幂函数的性质比较幂值大小的方法步骤.
第一步,据指数分清正负;
第二步,正数区分大于1与小于1的,a>1,α>0时,aα>1;0
第三步,构造幂函数应用幂函数单调性,特别注意含字母时,要注意底数不在同一单调区间内的情形.
2.给定一组数值,比较大小的步骤.
第一步:区分正负.一种情形是幂函数或指数函数值即幂式确定符号;另一种情形是对数式确定符号,要根据各自的性质进行.
第二步:正数通常还要区分大于1还是小于1.
第三步:同底的幂,用指数函数单调性;同指数的幂用幂函数单调性;同底的对数用对数函数单调性.
第四步:对于底数与指数均不相同的幂,或底数与真数均不相同的对数值大小的比较,通常是找一中间值过渡或化同底(化同指)、或放缩、有时作商(或作差)、或指对互化,对数式有时还用换底公式作变换等等.
