人教新课标高中数学B版必修1《2.1.3 函数的单调性》 课件(共21张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.1.3 函数的单调性》 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 774.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
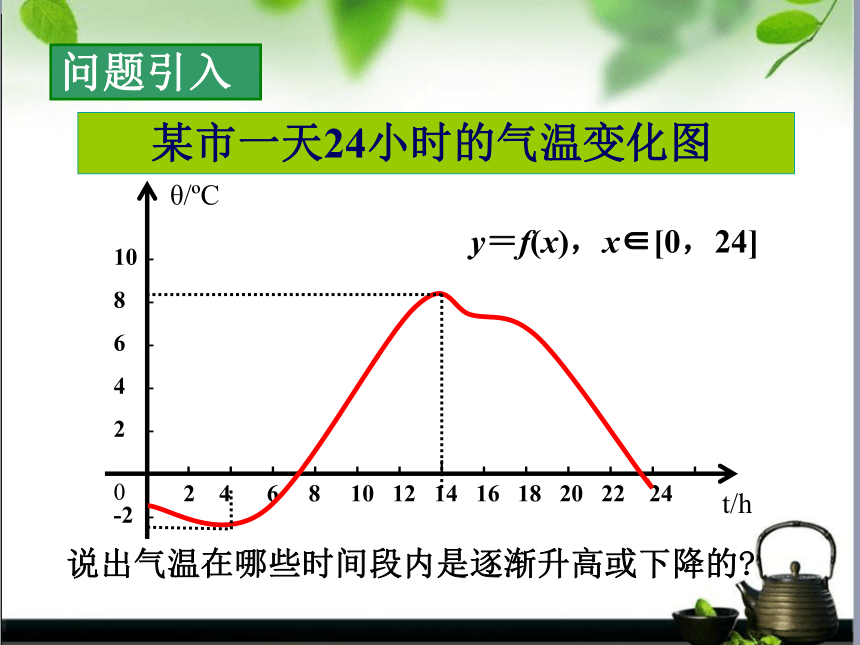
2 4 6 8 10 12 14 16 18 20 22 24
10
8
6
4
2
-2
0
θ/ C
t/h
某市一天24小时的气温变化图
y=f(x),x∈[0,24]
说出气温在哪些时间段内是逐渐升高或下降的
问题引入
能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?
x
y
o
x
y
o
x
y
o
局部上升或下降
下降
上升
O
x
y
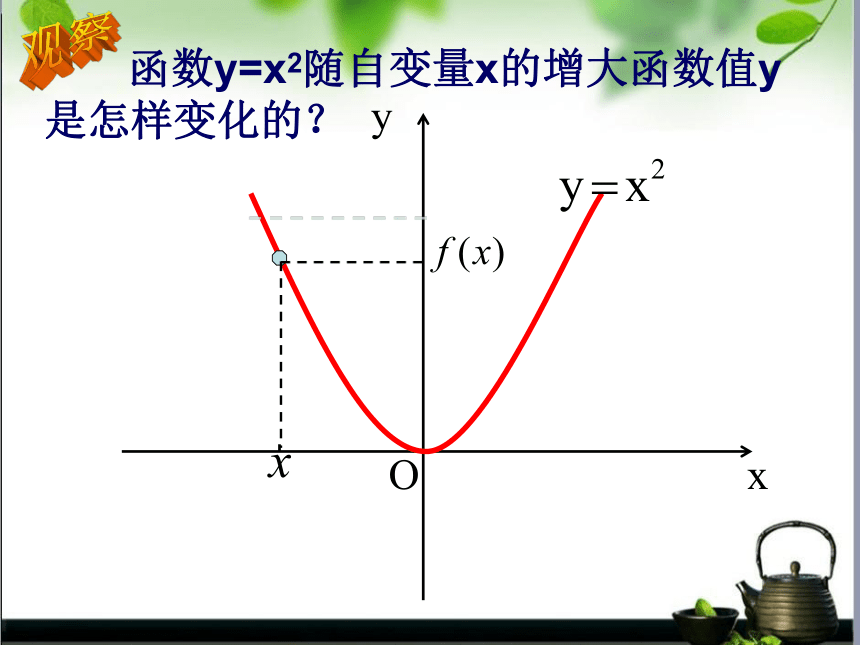
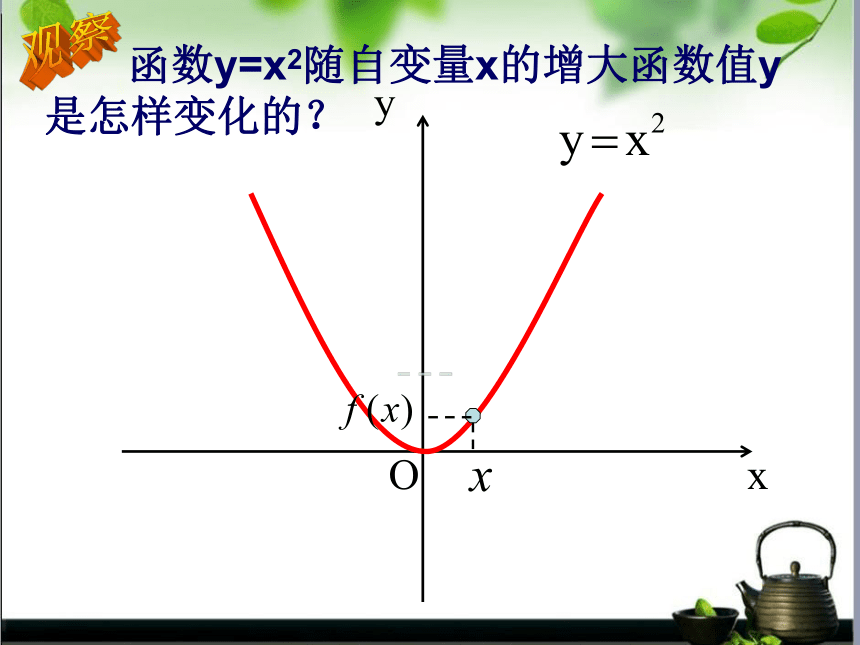
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
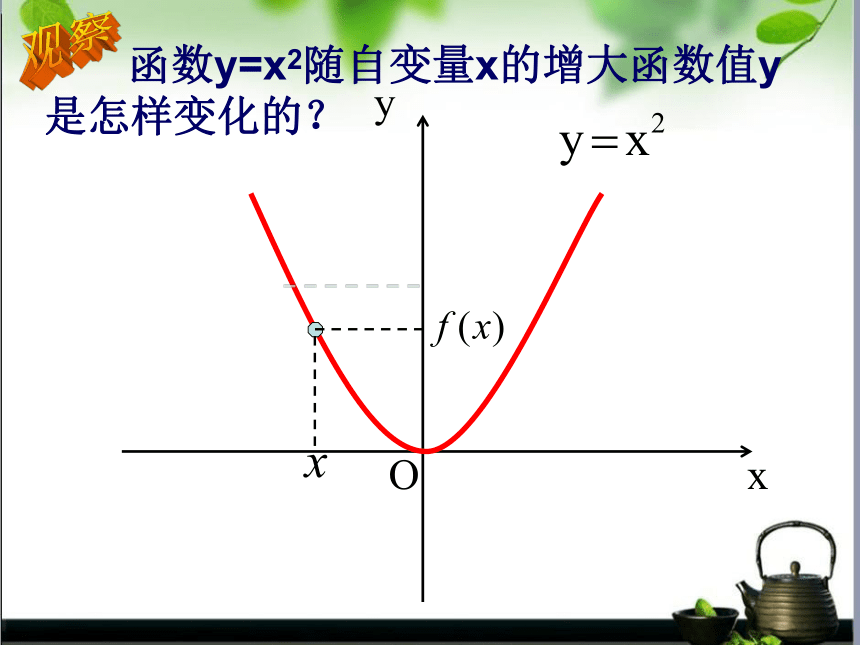
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
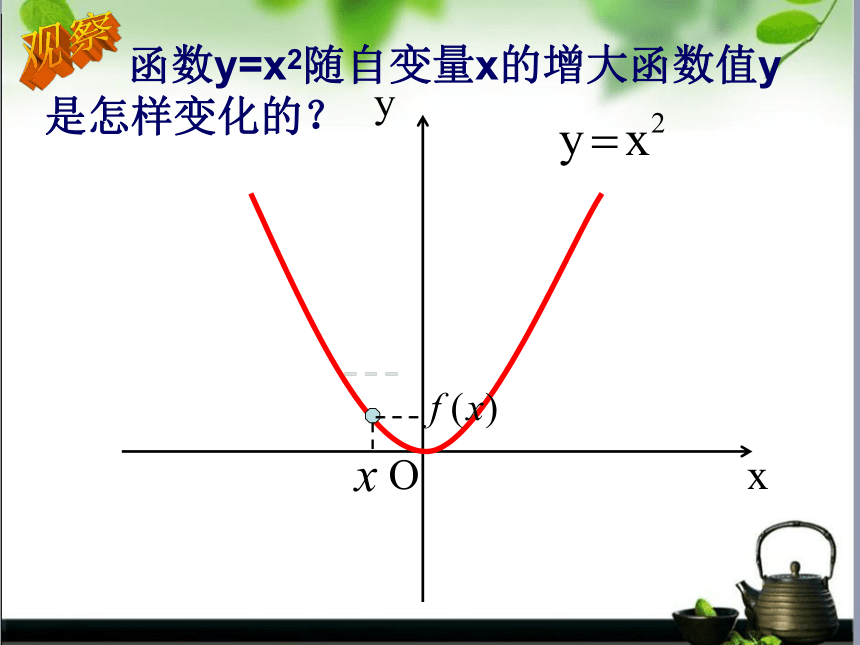
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
当x的值增大时,函数值y也增大
图像在该区间内逐渐上升
在某一区间内,
当x的值增大时,函数值y却减小
图像在该区间内逐渐下降
函数为该区间上的增函数
函数为该区间上的减函数
O
x
y
探索发现
O
x
y
x1
x2
f(x1)
f(x2)
通过之前的观察与研究,你能总结出增函数与减函数的定义吗?
x
O
y
x1
x2
f(x1)
f(x2)
如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,
就称函数y=f(x)在区间M上是增函数.
设函数y=f(x)的定义域为A,M A
设函数y=f(x)的定义域为A,M A
如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,
就称函数y=f(x)在区间M上是减函数.
(1)函数单调性是针对某个区间而言的,是一个局部性质;
比如:函数 f (x)满足 f (2)> f(1),则函数 f (x)在R 上是增函数.
(2) x 1, x 2 取值的任意性
y
x
O
1
2
f(1)
f(2)
(×)
例1、如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数。
-5
-2
1
3
5
f(x)
[-5,-2)
[-2,1)
[1,3)
[3,5]
x
y
o
强调: ①端点值的取舍
②单调区间之间用“,”或“和”
解:函数y=f(x)的单调区间有: [-5,-2), [-2,1),[1,3), [3,5]。
函数y=f(x)在 [-2,1), [3,5]为增函数;在 [-5,-2), [1,3)为减函数。
-5
典例探究
题型一、用图像法找函数的单调区间
典例探究
题型二、用定义法证明函数的单调性
证明函数单调性的步骤有哪些
1. 取值.任取x1,x2∈D,且x12. 作差.
3. 变形.(通分,因式分解和配方)
4. 定号.判断差f(x1)-f(x2)的正负
5. 判断.同增异减
主要步骤
典例探究
题型二、用定义法证明函数的单调性
1、 指出下列函数的单调区间:
2、试用定义法证明函数 在区间
上是单调递增函数。
课堂小结
请总结一下你这节课的收获
2 4 6 8 10 12 14 16 18 20 22 24
10
8
6
4
2
-2
0
θ/ C
t/h
某市一天24小时的气温变化图
y=f(x),x∈[0,24]
说出气温在哪些时间段内是逐渐升高或下降的
问题引入
能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?
x
y
o
x
y
o
x
y
o
局部上升或下降
下降
上升
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
O
x
y
函数y=x2随自变量x的增大函数值y
是怎样变化的?
当x的值增大时,函数值y也增大
图像在该区间内逐渐上升
在某一区间内,
当x的值增大时,函数值y却减小
图像在该区间内逐渐下降
函数为该区间上的增函数
函数为该区间上的减函数
O
x
y
探索发现
O
x
y
x1
x2
f(x1)
f(x2)
通过之前的观察与研究,你能总结出增函数与减函数的定义吗?
x
O
y
x1
x2
f(x1)
f(x2)
如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,
就称函数y=f(x)在区间M上是增函数.
设函数y=f(x)的定义域为A,M A
设函数y=f(x)的定义域为A,M A
如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,
就称函数y=f(x)在区间M上是减函数.
(1)函数单调性是针对某个区间而言的,是一个局部性质;
比如:函数 f (x)满足 f (2)> f(1),则函数 f (x)在R 上是增函数.
(2) x 1, x 2 取值的任意性
y
x
O
1
2
f(1)
f(2)
(×)
例1、如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数。
-5
-2
1
3
5
f(x)
[-5,-2)
[-2,1)
[1,3)
[3,5]
x
y
o
强调: ①端点值的取舍
②单调区间之间用“,”或“和”
解:函数y=f(x)的单调区间有: [-5,-2), [-2,1),[1,3), [3,5]。
函数y=f(x)在 [-2,1), [3,5]为增函数;在 [-5,-2), [1,3)为减函数。
-5
典例探究
题型一、用图像法找函数的单调区间
典例探究
题型二、用定义法证明函数的单调性
证明函数单调性的步骤有哪些
1. 取值.任取x1,x2∈D,且x1
3. 变形.(通分,因式分解和配方)
4. 定号.判断差f(x1)-f(x2)的正负
5. 判断.同增异减
主要步骤
典例探究
题型二、用定义法证明函数的单调性
1、 指出下列函数的单调区间:
2、试用定义法证明函数 在区间
上是单调递增函数。
课堂小结
请总结一下你这节课的收获
