人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》 课件(共15张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.1.4 函数的奇偶性》 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1017.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
精美的剪纸
复习引入
1 什么是轴对称图形?
2 什么是中心对称图形?
观察下面的函数图象:
f(x)=x
f(x)=x
f(x)=x
f(x)=x
f(x)=∣x∣
⑴
⑵
⑶
⑷
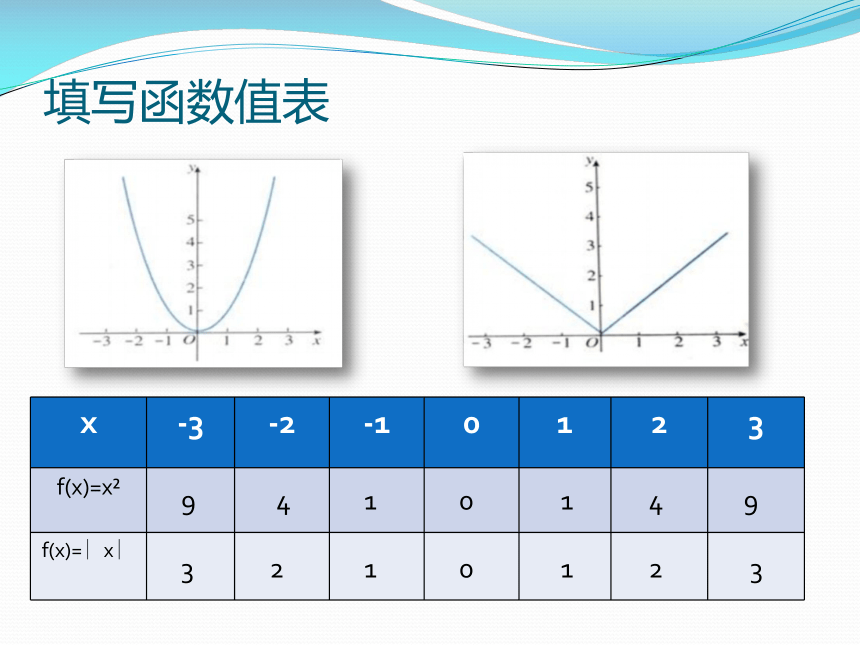
填写函数值表
x -3 -2 -1 0 1 2 3
f(x)=x
f(x)=∣x∣
9
4
1
0
1
4
9
3
2
1
0
1
2
3
x -3 -2 -1 0 1 2 3
-3
-2
-1
0
1
2
3
-1
不存在
1
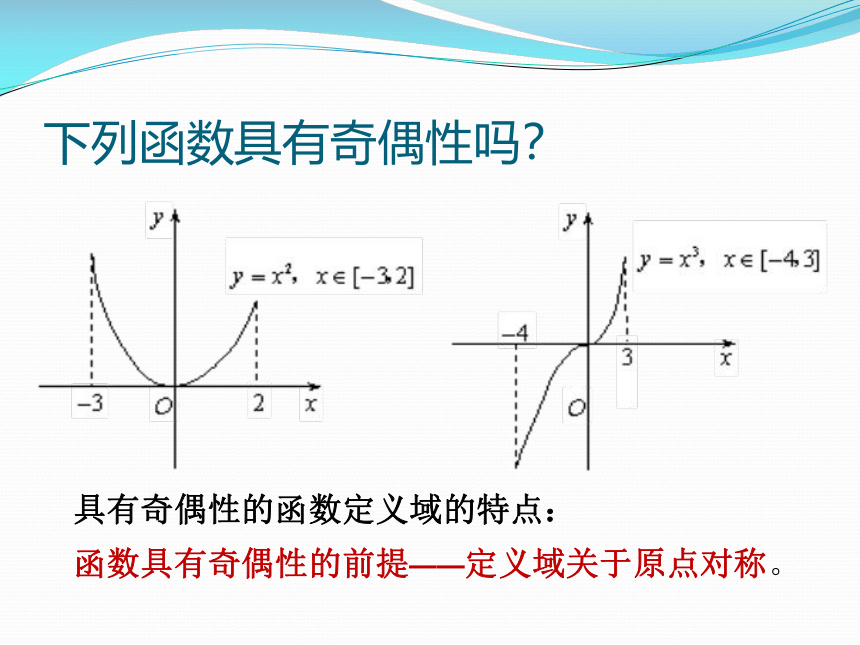
下列函数具有奇偶性吗?
具有奇偶性的函数定义域的特点:
函数具有奇偶性的前提——定义域关于原点对称。
1. 对于任意一个奇函数f(x),图象上的点P(x,f(x))关于原点的对称点 的坐标是什么?点 是否在f(x)的图象上?由此说明什么?
2. 如果函数的图象是以原点为对称中心的中心对称图形,能否判断它的奇偶性?
3.结合上述问题,你得出
什么结论?
如果一个函数是奇函数,那么它的图象关于原点对称;反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数。
如果一个函数是偶函数,那么它的图象关于y轴对称;反之,如果一个函数的图象关于y轴对称,那么这个函数是偶函数。
例1.判断下列函数的奇偶性
(1) =
⑶ ⑷
⑸
判断函数奇偶性的步骤:
第一步 确定函数的定义域,并判断其定义域是否关于
原点对称;
第二步 确定f(x)和f(-x) 的关系;
第三步 作出判断 :
(1)若f(-x)=f(x),则该函数为偶函数;
(2)若 f(-x)=-f(x),则该函数为奇函数;
(3)若 f(-x)=f(x)且f(-x)=-f(x), 则该函数 既是奇函数又是偶函数;
(4)若 f(-x)≠f(x)且f(-x) ≠ -f(x), 则该函数既不是奇函数也不是偶函数。
例2 (1)判断函数 的奇偶性;
(2)如图是函数 f(x) 图象的一部分,你能根据 f(x)的奇偶性画出它在y轴左边的图象吗?
随堂练习
设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解集是______.
小结:
1.函数奇偶性的定义.
2.奇函数和偶函数的图象性质.
3.函数奇偶性的分类.
4.函数奇偶性的判断方法.
作业:
必做题:1.试判断下列函数的奇偶性
拓展题:2.判断 函数f(x)=a(a是常数)的奇偶性。
3.已知函数 , 且f(-2) =10 ,求f(2)。
精美的剪纸
复习引入
1 什么是轴对称图形?
2 什么是中心对称图形?
观察下面的函数图象:
f(x)=x
f(x)=x
f(x)=x
f(x)=x
f(x)=∣x∣
⑴
⑵
⑶
⑷
填写函数值表
x -3 -2 -1 0 1 2 3
f(x)=x
f(x)=∣x∣
9
4
1
0
1
4
9
3
2
1
0
1
2
3
x -3 -2 -1 0 1 2 3
-3
-2
-1
0
1
2
3
-1
不存在
1
下列函数具有奇偶性吗?
具有奇偶性的函数定义域的特点:
函数具有奇偶性的前提——定义域关于原点对称。
1. 对于任意一个奇函数f(x),图象上的点P(x,f(x))关于原点的对称点 的坐标是什么?点 是否在f(x)的图象上?由此说明什么?
2. 如果函数的图象是以原点为对称中心的中心对称图形,能否判断它的奇偶性?
3.结合上述问题,你得出
什么结论?
如果一个函数是奇函数,那么它的图象关于原点对称;反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数。
如果一个函数是偶函数,那么它的图象关于y轴对称;反之,如果一个函数的图象关于y轴对称,那么这个函数是偶函数。
例1.判断下列函数的奇偶性
(1) =
⑶ ⑷
⑸
判断函数奇偶性的步骤:
第一步 确定函数的定义域,并判断其定义域是否关于
原点对称;
第二步 确定f(x)和f(-x) 的关系;
第三步 作出判断 :
(1)若f(-x)=f(x),则该函数为偶函数;
(2)若 f(-x)=-f(x),则该函数为奇函数;
(3)若 f(-x)=f(x)且f(-x)=-f(x), 则该函数 既是奇函数又是偶函数;
(4)若 f(-x)≠f(x)且f(-x) ≠ -f(x), 则该函数既不是奇函数也不是偶函数。
例2 (1)判断函数 的奇偶性;
(2)如图是函数 f(x) 图象的一部分,你能根据 f(x)的奇偶性画出它在y轴左边的图象吗?
随堂练习
设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解集是______.
小结:
1.函数奇偶性的定义.
2.奇函数和偶函数的图象性质.
3.函数奇偶性的分类.
4.函数奇偶性的判断方法.
作业:
必做题:1.试判断下列函数的奇偶性
拓展题:2.判断 函数f(x)=a(a是常数)的奇偶性。
3.已知函数 , 且f(-2) =10 ,求f(2)。
