人教新课标高中数学B版必修1《2.4.1 函数的零点》 课件(共15张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.4.1 函数的零点》 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 477.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
函数的零点
1.一元二次方程是否有实根的判定方法;
创设情境
2.二次函数y=ax2+bx+c的图像及其性质;
3.一元二次方程的根和函数与X轴交点的关系.
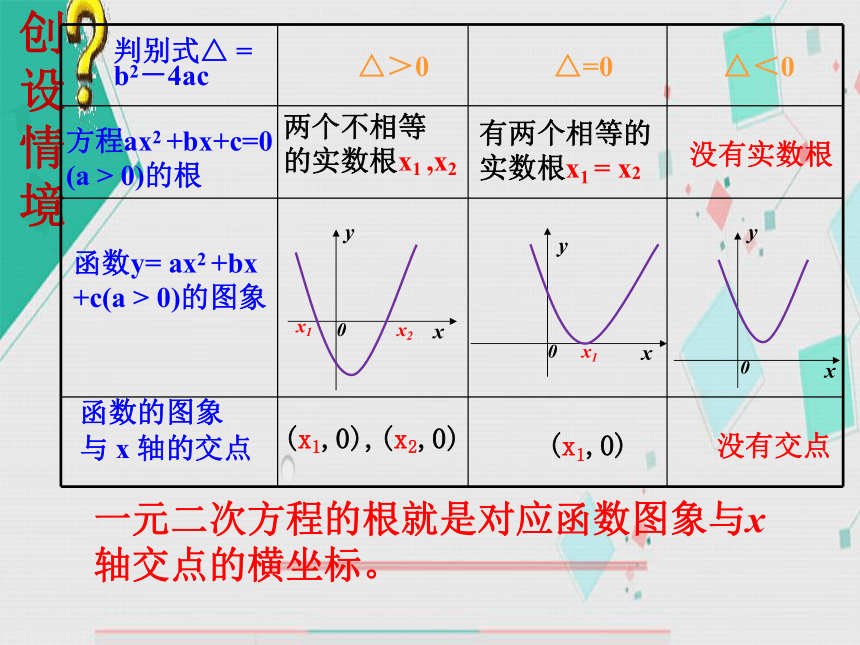
创设情境
方程ax2 +bx+c=0
(a > 0)的根
函数y= ax2 +bx
+c(a > 0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 ,x2
一元二次方程的根就是对应函数图象与x轴交点的横坐标。
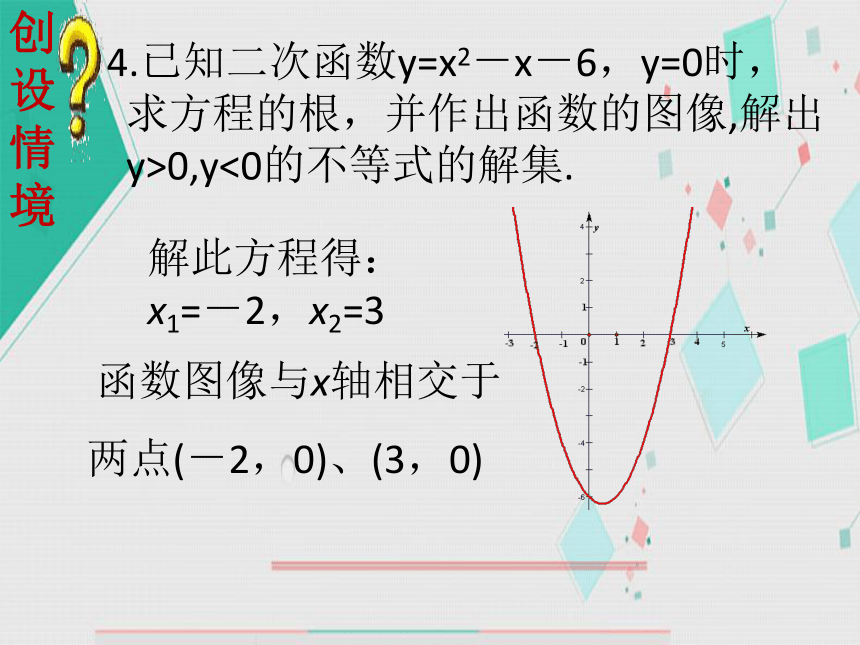
4.已知二次函数y=x2-x-6,y=0时,
求方程的根,并作出函数的图像,解出
y>0,y<0的不等式的解集.
创设情境
解此方程得:
x1=-2,x2=3
函数图像与x轴相交于两点(-2,0)、(3,0)
新知探究
概念形成:
一般地,如果函数y=f(x)在实数
a 处的值等于零,即f(a)=0,则a叫做
这个函数的零点.
概念深化:
1.函数的零点并不是“点”,而是
实数;
2.函数y=f(x)的零点就是方程f(x)=0
的实数根,亦即函数图像与x轴交点
的横坐标,也是不等式f(x)>0(<0)
的端点值.
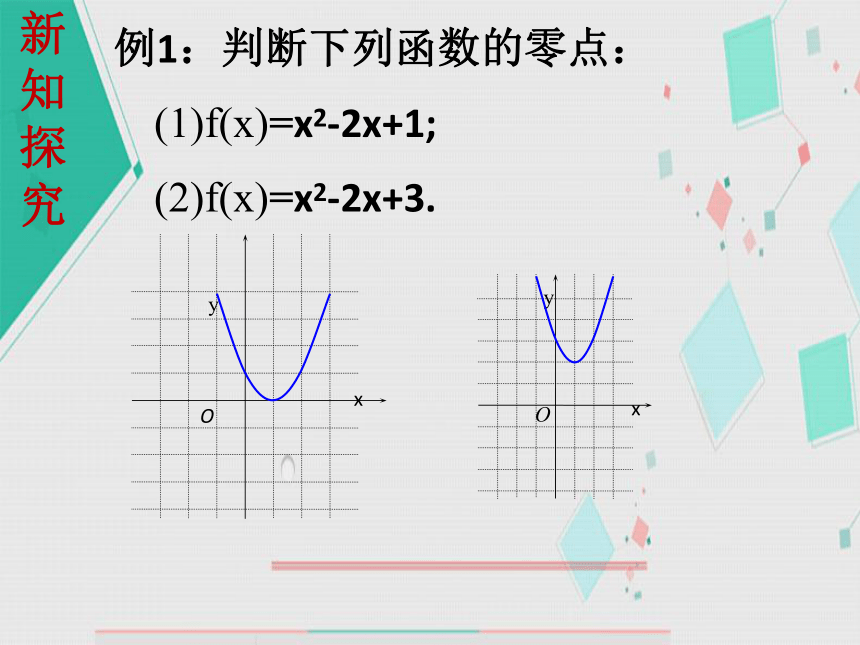
(1)f(x)=x2-2x+1;
x
y
O
(2)f(x)=x2-2x+3.
例1:判断下列函数的零点:
x
O
y
新知探究
例2:求函数f(x)=-x2-2x+3
的零点,并指出y>0,y<0时
x的取值范围.
0
x
y
新知探究
判别式 方程的根 函数的零点个数
△>0 两个不相等的实根 2个(变号零点)
△=0 两个相等的实根 1个二重(二阶)零点
△<0 无实根 无零点
二次函数y=ax2+bx+c的零点个数,方程ax2+bx+c=0的实根个数见下表:
新知探究
零点的存在性:
x
y
O
a
b
c
d
观察下面函数y=f(x)的图象:
①在区间[a,b]上 (有/无)零点,f(a)·f(b)____0(<,>)
②在区间[b,c]上 (有/无)零点,f(b)·f(c)____0(<,>)
新知探究
如果函数 y=f(x)在区间[a, b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0, 那么, 函数y=f(x) 在区间(a, b)内至少有一个零点, 即存在c∈(a, b),使f(c)=0, 这个c也就是方程f(x) = 0的根.
定理
例:函数f(x)=x3+x-3,则函数f(x)的零点所在区间( )
A.(-1,0) B.(0,1) C.(1,2) D. (2,3)
典例探究
思维迁移
(四)利用零点作函数图象:
作函数f(x)=x3-2x2-x+2的图象
(2)
;
作函数
的图象
作函数 的图象
变式探究:
函数零点的概念
零点的存在性
求零点及零点所在区间
利用函数零点的性质作函数图像
课堂小结
拓展延伸
2.函数
零点位于区间( )
A.
B.
C.
D.
1.求函数
的零点个数.
教材72页A组5,6题;
B组1题(3),2题.
课后作业
函数的零点
1.一元二次方程是否有实根的判定方法;
创设情境
2.二次函数y=ax2+bx+c的图像及其性质;
3.一元二次方程的根和函数与X轴交点的关系.
创设情境
方程ax2 +bx+c=0
(a > 0)的根
函数y= ax2 +bx
+c(a > 0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 ,x2
一元二次方程的根就是对应函数图象与x轴交点的横坐标。
4.已知二次函数y=x2-x-6,y=0时,
求方程的根,并作出函数的图像,解出
y>0,y<0的不等式的解集.
创设情境
解此方程得:
x1=-2,x2=3
函数图像与x轴相交于两点(-2,0)、(3,0)
新知探究
概念形成:
一般地,如果函数y=f(x)在实数
a 处的值等于零,即f(a)=0,则a叫做
这个函数的零点.
概念深化:
1.函数的零点并不是“点”,而是
实数;
2.函数y=f(x)的零点就是方程f(x)=0
的实数根,亦即函数图像与x轴交点
的横坐标,也是不等式f(x)>0(<0)
的端点值.
(1)f(x)=x2-2x+1;
x
y
O
(2)f(x)=x2-2x+3.
例1:判断下列函数的零点:
x
O
y
新知探究
例2:求函数f(x)=-x2-2x+3
的零点,并指出y>0,y<0时
x的取值范围.
0
x
y
新知探究
判别式 方程的根 函数的零点个数
△>0 两个不相等的实根 2个(变号零点)
△=0 两个相等的实根 1个二重(二阶)零点
△<0 无实根 无零点
二次函数y=ax2+bx+c的零点个数,方程ax2+bx+c=0的实根个数见下表:
新知探究
零点的存在性:
x
y
O
a
b
c
d
观察下面函数y=f(x)的图象:
①在区间[a,b]上 (有/无)零点,f(a)·f(b)____0(<,>)
②在区间[b,c]上 (有/无)零点,f(b)·f(c)____0(<,>)
新知探究
如果函数 y=f(x)在区间[a, b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0, 那么, 函数y=f(x) 在区间(a, b)内至少有一个零点, 即存在c∈(a, b),使f(c)=0, 这个c也就是方程f(x) = 0的根.
定理
例:函数f(x)=x3+x-3,则函数f(x)的零点所在区间( )
A.(-1,0) B.(0,1) C.(1,2) D. (2,3)
典例探究
思维迁移
(四)利用零点作函数图象:
作函数f(x)=x3-2x2-x+2的图象
(2)
;
作函数
的图象
作函数 的图象
变式探究:
函数零点的概念
零点的存在性
求零点及零点所在区间
利用函数零点的性质作函数图像
课堂小结
拓展延伸
2.函数
零点位于区间( )
A.
B.
C.
D.
1.求函数
的零点个数.
教材72页A组5,6题;
B组1题(3),2题.
课后作业
