人教新课标高中数学B版必修1《2.4.2 求函数零点近似解的一种计算方法——二分法》 课件(共15张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《2.4.2 求函数零点近似解的一种计算方法——二分法》 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 16:51:36 | ||
图片预览






文档简介
(共15张PPT)
1
2.4.2求函数零点近似解的
一种方法——二分法
请每位同学从(0,64)
中任选一个整数,记在心
里,我提六个问题,你只
要回答我“高了”还是“低了”
。六个问题全答完以后,
我就会算出你心里记的那
个数。
探求新知
想一想,下列函数是否存在零点?你用什么方法求得零点?
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
探求新知
2
3
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
探求新知
零点所在区 间(a,b) 区间端点函数值符号
中点值c
f(c)近似值
区间长|a-b|
2.5
2.75
2.625
2.5625
2.53125
f(2.5) <0
f(2.75) >0
f(2.625) >0
f(2.5625) >0
f(2.53125) <0
(2,3)
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
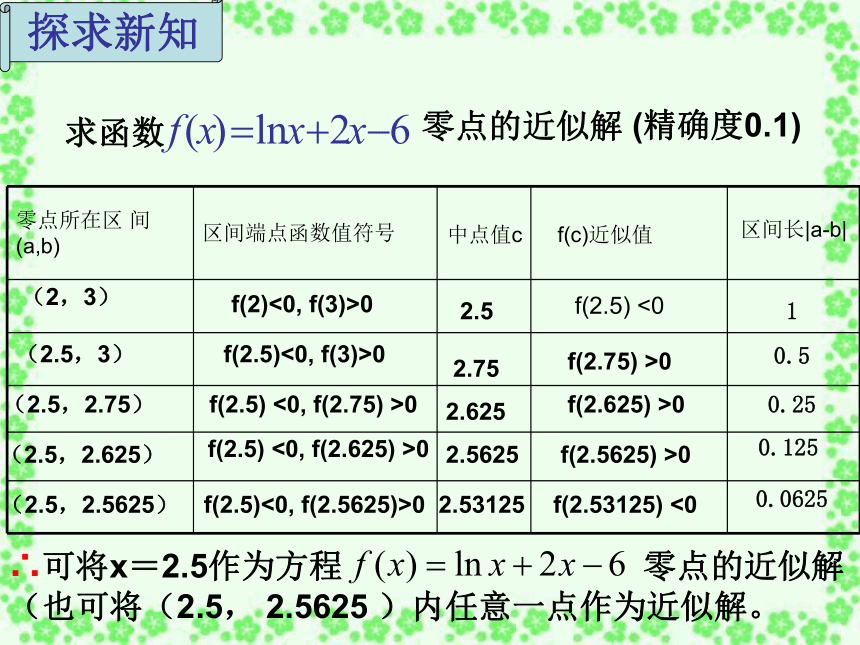
(精确度0.1)
求函数
零点的近似解
1
0.5
0.25
0.125
0.0625
∴可将x=2.5作为方程 零点的近似解(也可将(2.5, 2.5625 )内任意一点作为近似解。
f(2)<0, f(3)>0
f(2.5) <0, f(2.625) >0
f(2.5)<0, f(3)>0
f(2.5) <0, f(2.75) >0
f(2.5)<0, f(2.5625)>0
探求新知
二分法的定义:
形成概念
C
x
y
0
x
y
0
x
y
0
x
y
0
A
B
C
D
练习1: 下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )
4.判断是否达到精确度 :即若|a-b|< , 则得到零点近似值a(或b);否则重复2~4.
(2)若f(a)f(c)<0,则零点
(3)若f(c)f(b)<0,则零点
(1)若f(c)=0,则c就是函数的零点;
3.计算f(c);
2.求区间(a,b)的中点c;(其中c= )
2
b
a
+
a
b
c
用二分法求函数f(x)零点近似值的步骤:
总结方法
易知 f(1)=-2<0,f(2)=6>0
∴ 原方程的近似解为1.4375
设其零点为
令
,
,
7
3
2
)
(
0
x
x
x
f
x
-
+
=
巩固新知
例1 利用计算器求函数
的一个正实数零点(精确到0.1)
解:
学以致用
2、根据表格中的数据,可以断定方程
的一个根所在区间是________.
x -1 0 1 2 3
0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
(1,2)
在26枚崭新的金币中,混入了一枚外表与它们相同的假币(重量较轻),现在只有一台天平,请问:最多几次就可以发现这枚假币?
思考
函数
方程
转化思想
逼近思想
数学
源于生活
数学
用于生活
二分法
数形结合
1.确定初始区间
2.不断分解区间
3.根据精确度得出近似解
用二分法求
函数零点的近似解
归纳总结
课后作业:
课本 第74页 习题1,2
拓展作业:
搜集二分法在实际
生活中的应用实例
布置作业
周而复始怎么办 精确度上来判断.
定区间,找中点, 中值计算两边看.
同号去,异号算, 零点落在异号间.
口 诀
1
2.4.2求函数零点近似解的
一种方法——二分法
请每位同学从(0,64)
中任选一个整数,记在心
里,我提六个问题,你只
要回答我“高了”还是“低了”
。六个问题全答完以后,
我就会算出你心里记的那
个数。
探求新知
想一想,下列函数是否存在零点?你用什么方法求得零点?
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
探求新知
2
3
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
探求新知
零点所在区 间(a,b) 区间端点函数值符号
中点值c
f(c)近似值
区间长|a-b|
2.5
2.75
2.625
2.5625
2.53125
f(2.5) <0
f(2.75) >0
f(2.625) >0
f(2.5625) >0
f(2.53125) <0
(2,3)
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(精确度0.1)
求函数
零点的近似解
1
0.5
0.25
0.125
0.0625
∴可将x=2.5作为方程 零点的近似解(也可将(2.5, 2.5625 )内任意一点作为近似解。
f(2)<0, f(3)>0
f(2.5) <0, f(2.625) >0
f(2.5)<0, f(3)>0
f(2.5) <0, f(2.75) >0
f(2.5)<0, f(2.5625)>0
探求新知
二分法的定义:
形成概念
C
x
y
0
x
y
0
x
y
0
x
y
0
A
B
C
D
练习1: 下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )
4.判断是否达到精确度 :即若|a-b|< , 则得到零点近似值a(或b);否则重复2~4.
(2)若f(a)f(c)<0,则零点
(3)若f(c)f(b)<0,则零点
(1)若f(c)=0,则c就是函数的零点;
3.计算f(c);
2.求区间(a,b)的中点c;(其中c= )
2
b
a
+
a
b
c
用二分法求函数f(x)零点近似值的步骤:
总结方法
易知 f(1)=-2<0,f(2)=6>0
∴ 原方程的近似解为1.4375
设其零点为
令
,
,
7
3
2
)
(
0
x
x
x
f
x
-
+
=
巩固新知
例1 利用计算器求函数
的一个正实数零点(精确到0.1)
解:
学以致用
2、根据表格中的数据,可以断定方程
的一个根所在区间是________.
x -1 0 1 2 3
0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
(1,2)
在26枚崭新的金币中,混入了一枚外表与它们相同的假币(重量较轻),现在只有一台天平,请问:最多几次就可以发现这枚假币?
思考
函数
方程
转化思想
逼近思想
数学
源于生活
数学
用于生活
二分法
数形结合
1.确定初始区间
2.不断分解区间
3.根据精确度得出近似解
用二分法求
函数零点的近似解
归纳总结
课后作业:
课本 第74页 习题1,2
拓展作业:
搜集二分法在实际
生活中的应用实例
布置作业
周而复始怎么办 精确度上来判断.
定区间,找中点, 中值计算两边看.
同号去,异号算, 零点落在异号间.
口 诀
