人教新课标高中数学B版必修1《3.2.3 指数函数与对数函数的关系》 课件(共23张PPT)
文档属性
| 名称 | 人教新课标高中数学B版必修1《3.2.3 指数函数与对数函数的关系》 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 16:55:50 | ||
图片预览








文档简介
(共23张PPT)
3.2.3 指数函数与对数
函数的关系
知识与技能:
1、知识目标:
使学生能正确比较指数函数和对数函数性质关系,能以它们为例
对反函数进行解释和直观理解。
2、能力目标:
从观察图像到引出概念,培养学生观察、分析、探究问题的能力,
数形结合思想的运用能力,提高由特殊到一般的归纳概括能力。
情感、态度与价值观:
引导学生发现指数函数与对数函数的对立统一关系,并欣赏数形
和谐的对称美。
重点与难点:
1、重点:对指数函数和对数函数性质关系的比较,及对反函数
概念的理解。
2、难点:反函数的概念。
问题1:以上图片有一个共同特点,是什么?
一、新课引入(发现对称):
0
1
1
x
y
o
1 2 3 4 5 6 7 8
-1
-2
-3
3
2
1
结论?
问题2:观察两个对应值表、两组点的坐标、两组点的位置、两个函数图像之间的关系?通过对比你得到什么结论?
x … -3 -2 -1 0 1 2 3 …
y … 1/8 1/4 1/2 1 2 4 8 …
x … 1/8 1/4 1/2 1 2 4 8 …
y … -3 -2 -1 0 1 2 3 …
表1 y=2x
表2 y=log2x
0
1
1
y=x
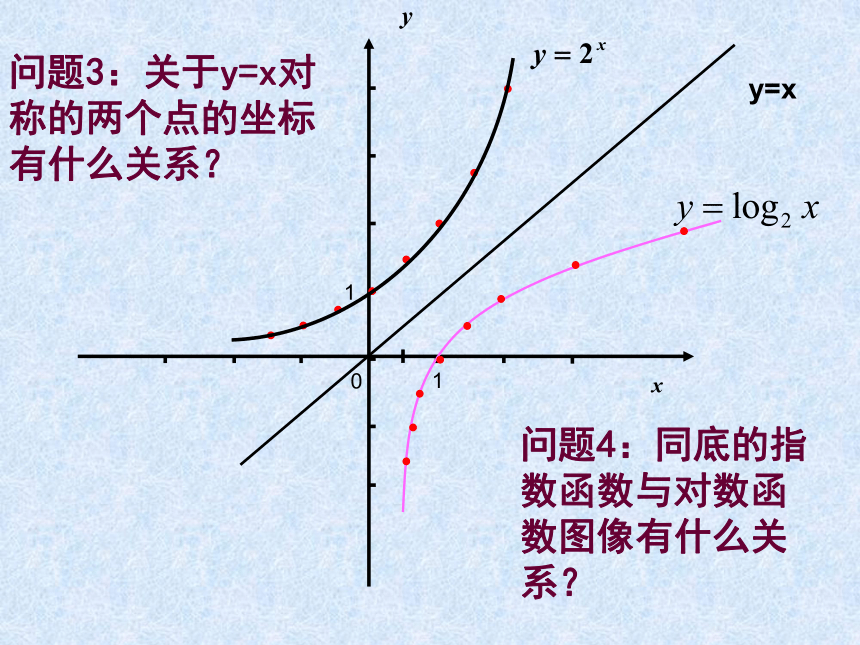
问题3:关于y=x对称的两个点的坐标有什么关系?
问题4:同底的指数函数与对数函数图像有什么关系?
二、新课讲授(解释对称):
问题5:指数函数 与
对数函数 有何内在联系?
互化
x、y互换
探究:这种关系是否具有一般性?
强调:指数式与对数式互化图像不变,x,y互换引起图像关于直线y=x对称
问题6:第一步变换有没有引起图像变化?为什么?
问题7:第二步变换有没有引起图像变化?为什么?
结论?
互化
x、y互换
指数函数与对数函数之间的这种关系并不是
它们所特有的,有大量的函数之间具有这种
关系。我们称它们互为反函数。
反函数的定义:当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数。
函数y=f(x)(x∈A)的反函数.
三、明确定义:
记:y= f -1 ( x )
(1) 反函数的定义域与值域正好是原来函数的值
域与定义域。如: 不是函数 的反
函数,因为前者的值域显然不是后者的定义域。
(3) 反函数也是函数,因为他们符合函数的定义。
(2) 对任意一个函数y=f(x),不一定总有反函数;只有当确定一个函数的映射是一一映射时,这个函数才存在反函数。如果有反函数,那么原来函数也是反函数的反函数,即他们互为反函数
概念深化:
问题8:如何求函数的反函数?
求反函数的方法步骤:
1)求出原函数的值域;即求出反函数的定义域;
2)由 y = f ( x ) 反解出 x = f -1 ( y );即把 x 用 y 表 示出来;
3)将 x = f -1 ( y ) 改写成 y = f -1 ( x ),并写出反函数的定义域;即对调 x = f -1 ( y ) 中的 x、y.
[例1] 求下列函数的反函数:
首先,将y = (x)看作方程,解出x= -1(y) (y∈C);
其次,将x,y互换,得到y= -1(x) (x∈C) .
最后,指出反函数的定义域
结论
四、巩固训练,加深概念:
同底的指数函数与对数函数互为反函数
( )
A. y轴对称 B. x轴对称
C. 原点对称 D. 直线y=x对称
[例2]函数y=3x的图象与函数y=log3x的
图象关于
D
结论
函数 y = f ( x ) 的图象与它的反函数
y = f -1 ( x ) 的图象关于直线 y = x 对称。
[例3] 已知函数 .
(
求证函数y=f(x)的图象关于直线y=x对称.
因f(x)的反函数与原函数相同,故结论成立.
证明:
探究:如何证明一个函数的图象本身关于直线y=x对称?
结论
证明一个函数的图象关于直线y=x对称,
只需说明它的反函数与原函数相同
[例4]函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值.
若函数y=f(x)的图象经过点(a, b),
则其反函数的图象经过点(b, a).
结论?
解:依题意,得
若函数y=f(x)存在反函数,
且f-1(a)=b,则f(b)=a
结论?
互为反函数的两个函数定义域、值域互换。
练习:求下列函数的反函数:
x 0 1 2 3
y 0 1 4 9
问题9:练习中函数与函数
x -3 -2 -1 0 1 2 3
y 9 4 1 0 1 4 9
比较,有何异同?
结论?
只有一一映射的函数才有反函数
五、互为反函数的函数图象增减速度比较:
问题10:两个函数图象
在第一象限增长速度有
何关系?
归纳小结:同底的指数函数和对数函数性质关系对照表:
性质 性质关系
图像 1.关于y=x对称
定义域
值域
特殊点
单调性
增减速度
指数
指数
指数
指数
对数
对数
对数
对数
2.定义域、值域
互换
3.横、纵坐标互换
4.单调性不变
5.增减速度一快一慢
注意:同底的指数函数和对数函数性质关系,也体现了
所有互为反函数的两函数间性质关系
布置作业:
1.教材第106页练习A第2题;第107页练习B第1、2题;
2.教材第118页“思考与交流”的第6题
课后思考:
1.为什么同底的指数函数和对数函数单调性一致?
2.为什么同底的指数函数和对数函数增减速度一快一慢?
提示:运用函数单调性定义和反函数定义解释
3.2.3 指数函数与对数
函数的关系
知识与技能:
1、知识目标:
使学生能正确比较指数函数和对数函数性质关系,能以它们为例
对反函数进行解释和直观理解。
2、能力目标:
从观察图像到引出概念,培养学生观察、分析、探究问题的能力,
数形结合思想的运用能力,提高由特殊到一般的归纳概括能力。
情感、态度与价值观:
引导学生发现指数函数与对数函数的对立统一关系,并欣赏数形
和谐的对称美。
重点与难点:
1、重点:对指数函数和对数函数性质关系的比较,及对反函数
概念的理解。
2、难点:反函数的概念。
问题1:以上图片有一个共同特点,是什么?
一、新课引入(发现对称):
0
1
1
x
y
o
1 2 3 4 5 6 7 8
-1
-2
-3
3
2
1
结论?
问题2:观察两个对应值表、两组点的坐标、两组点的位置、两个函数图像之间的关系?通过对比你得到什么结论?
x … -3 -2 -1 0 1 2 3 …
y … 1/8 1/4 1/2 1 2 4 8 …
x … 1/8 1/4 1/2 1 2 4 8 …
y … -3 -2 -1 0 1 2 3 …
表1 y=2x
表2 y=log2x
0
1
1
y=x
问题3:关于y=x对称的两个点的坐标有什么关系?
问题4:同底的指数函数与对数函数图像有什么关系?
二、新课讲授(解释对称):
问题5:指数函数 与
对数函数 有何内在联系?
互化
x、y互换
探究:这种关系是否具有一般性?
强调:指数式与对数式互化图像不变,x,y互换引起图像关于直线y=x对称
问题6:第一步变换有没有引起图像变化?为什么?
问题7:第二步变换有没有引起图像变化?为什么?
结论?
互化
x、y互换
指数函数与对数函数之间的这种关系并不是
它们所特有的,有大量的函数之间具有这种
关系。我们称它们互为反函数。
反函数的定义:当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数。
函数y=f(x)(x∈A)的反函数.
三、明确定义:
记:y= f -1 ( x )
(1) 反函数的定义域与值域正好是原来函数的值
域与定义域。如: 不是函数 的反
函数,因为前者的值域显然不是后者的定义域。
(3) 反函数也是函数,因为他们符合函数的定义。
(2) 对任意一个函数y=f(x),不一定总有反函数;只有当确定一个函数的映射是一一映射时,这个函数才存在反函数。如果有反函数,那么原来函数也是反函数的反函数,即他们互为反函数
概念深化:
问题8:如何求函数的反函数?
求反函数的方法步骤:
1)求出原函数的值域;即求出反函数的定义域;
2)由 y = f ( x ) 反解出 x = f -1 ( y );即把 x 用 y 表 示出来;
3)将 x = f -1 ( y ) 改写成 y = f -1 ( x ),并写出反函数的定义域;即对调 x = f -1 ( y ) 中的 x、y.
[例1] 求下列函数的反函数:
首先,将y = (x)看作方程,解出x= -1(y) (y∈C);
其次,将x,y互换,得到y= -1(x) (x∈C) .
最后,指出反函数的定义域
结论
四、巩固训练,加深概念:
同底的指数函数与对数函数互为反函数
( )
A. y轴对称 B. x轴对称
C. 原点对称 D. 直线y=x对称
[例2]函数y=3x的图象与函数y=log3x的
图象关于
D
结论
函数 y = f ( x ) 的图象与它的反函数
y = f -1 ( x ) 的图象关于直线 y = x 对称。
[例3] 已知函数 .
(
求证函数y=f(x)的图象关于直线y=x对称.
因f(x)的反函数与原函数相同,故结论成立.
证明:
探究:如何证明一个函数的图象本身关于直线y=x对称?
结论
证明一个函数的图象关于直线y=x对称,
只需说明它的反函数与原函数相同
[例4]函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值.
若函数y=f(x)的图象经过点(a, b),
则其反函数的图象经过点(b, a).
结论?
解:依题意,得
若函数y=f(x)存在反函数,
且f-1(a)=b,则f(b)=a
结论?
互为反函数的两个函数定义域、值域互换。
练习:求下列函数的反函数:
x 0 1 2 3
y 0 1 4 9
问题9:练习中函数与函数
x -3 -2 -1 0 1 2 3
y 9 4 1 0 1 4 9
比较,有何异同?
结论?
只有一一映射的函数才有反函数
五、互为反函数的函数图象增减速度比较:
问题10:两个函数图象
在第一象限增长速度有
何关系?
归纳小结:同底的指数函数和对数函数性质关系对照表:
性质 性质关系
图像 1.关于y=x对称
定义域
值域
特殊点
单调性
增减速度
指数
指数
指数
指数
对数
对数
对数
对数
2.定义域、值域
互换
3.横、纵坐标互换
4.单调性不变
5.增减速度一快一慢
注意:同底的指数函数和对数函数性质关系,也体现了
所有互为反函数的两函数间性质关系
布置作业:
1.教材第106页练习A第2题;第107页练习B第1、2题;
2.教材第118页“思考与交流”的第6题
课后思考:
1.为什么同底的指数函数和对数函数单调性一致?
2.为什么同底的指数函数和对数函数增减速度一快一慢?
提示:运用函数单调性定义和反函数定义解释
