1.4.2用空间向量研究距离、夹角问题: 线面角(中档) 同步练习(Word版含解析)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题: 线面角(中档) 同步练习(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 612.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览


文档简介
《空间向量》专题9-1 线面角(中档)
(4套,4页,含答案)
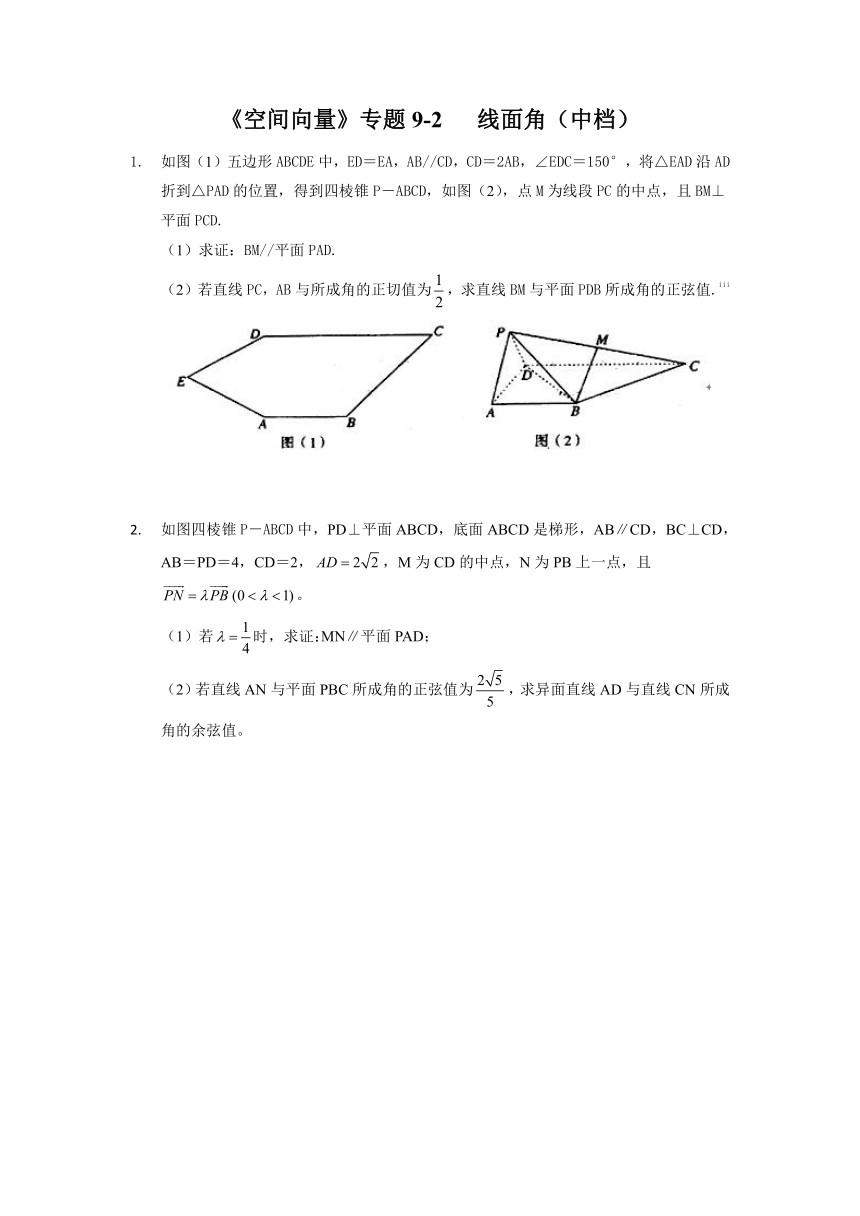
如图(1),在边长为2的正方形ABCD中,E是边AB的中点.将△ADE沿DE折起,如图(2),F是折叠后AC的中点.
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若平面ADE⊥平面BCDE,求BF与平面ABD所成角的正弦值.[endnoteRef:0]
[0: 答案:证明略,;
【解析】(Ⅰ)取AD中点G,连结EG,FG,
∵F为AC中点, ∴FG綊CD,BE綊CD
∴FG綊BE,从而四边形EBFG是平行四边形.(3分)
∴BF∥EG,又BF?平面ADE,EG?平面ADE,
∴BF ∥平面ADE.(5分)
(Ⅱ) 如图所示以B为坐标原点,建立空间直角坐标系,在图(1)中作AH⊥DE于H,易求得EH=,AH=,
作HN⊥AE于N,HM⊥BC于M,则HN=,HM=,
所以A.(7分)
而B(0,0,0),D(2,2,0),则=,=(2,2,0).
设平面ABD的法向量为n=(x,y,z),
则?
解得一个法向量为n=(-,,-2).(9分)
又C(2,0,0),∴F,∴=,
∵cos〈n,〉==-.
∴BF与平面ABD所成角的正弦值为.(12分)
]
如图,在各棱长均为2的正三棱柱ABC-A1B1C1中,D,E分别为棱A1B1与BB1的中点,M,N为线段C1D上的动点,其中,M更靠近D,且MN=C1N.
(1)证明:A1E⊥平面AC1D;
(2)若NE与平面BCC1B1所成角的正弦值为,求异面直线BM与NE所成角的余弦值.[endnoteRef:1]
[1: 答案:证明略,;
(1)证明:由已知得为正三角形,为棱的中点,
∴,
在正三棱柱中,底面,则.
又,∴平面,∴.
易证,又,∴平面.
(2)解:取的中点,的中点,则,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,,,,
设,
则,
易知是平面的一个法向量,
∴,解得.
∴,,,,
∴,
∴异面直线与所成角的余弦值为.
]
《空间向量》专题9-2 线面角(中档)
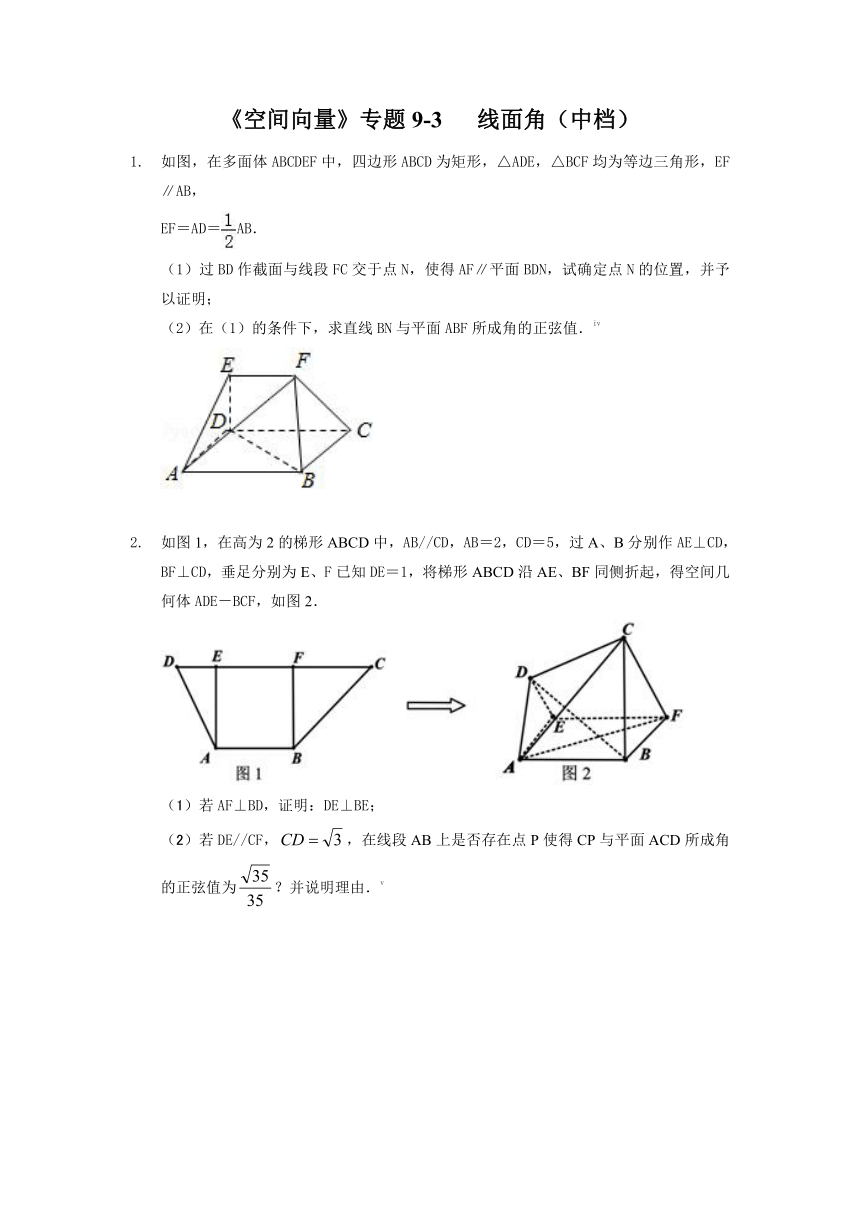
如图(1)五边形ABCDE中,ED=EA,AB//CD,CD=2AB,∠EDC=150°,将△EAD沿AD折到△PAD的位置,得到四棱锥P-ABCD,如图(2),点M为线段PC的中点,且BM⊥平面PCD.
(1)求证:BM//平面PAD.
(2)若直线PC,AB与所成角的正切值为,求直线BM与平面PDB所成角的正弦值.[endnoteRef:2]
[2: 答案:证明略,;
(1)证明:取的中点,连接,则,
又,所以,………………………………2分
则四边形为平行四边形,所以,……………………………………3分
又因为面
所以平面……………………………………………………………………5分
(2)又平面,
∴平面,∴.
由即及为的中点,可得为等边三角形,
∴,又,∴,∴,
∴平面平面,
∴平面平面.………………………………………………………………6分
,∴为直线与所成的角,
由(1)可得,∴,∴,
设,则,
取的中点,连接,过作的平行线,
可建立如图所示的空间直角坐标系,
则,
∴,…………………………………………………………………9分
所以,
设为平面的法向量,则,即,
取,则为平面的一个法向量,
∵,
则直线与平面所成角的正弦值为.………………………………12分
]
如图四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是梯形,AB∥CD,BC⊥CD,AB=PD=4,CD=2,,M为CD的中点,N为PB上一点,且。
(1)若MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为,求异面直线AD与直线CN所成角的余弦值。
《空间向量》专题9-3 线面角(中档)
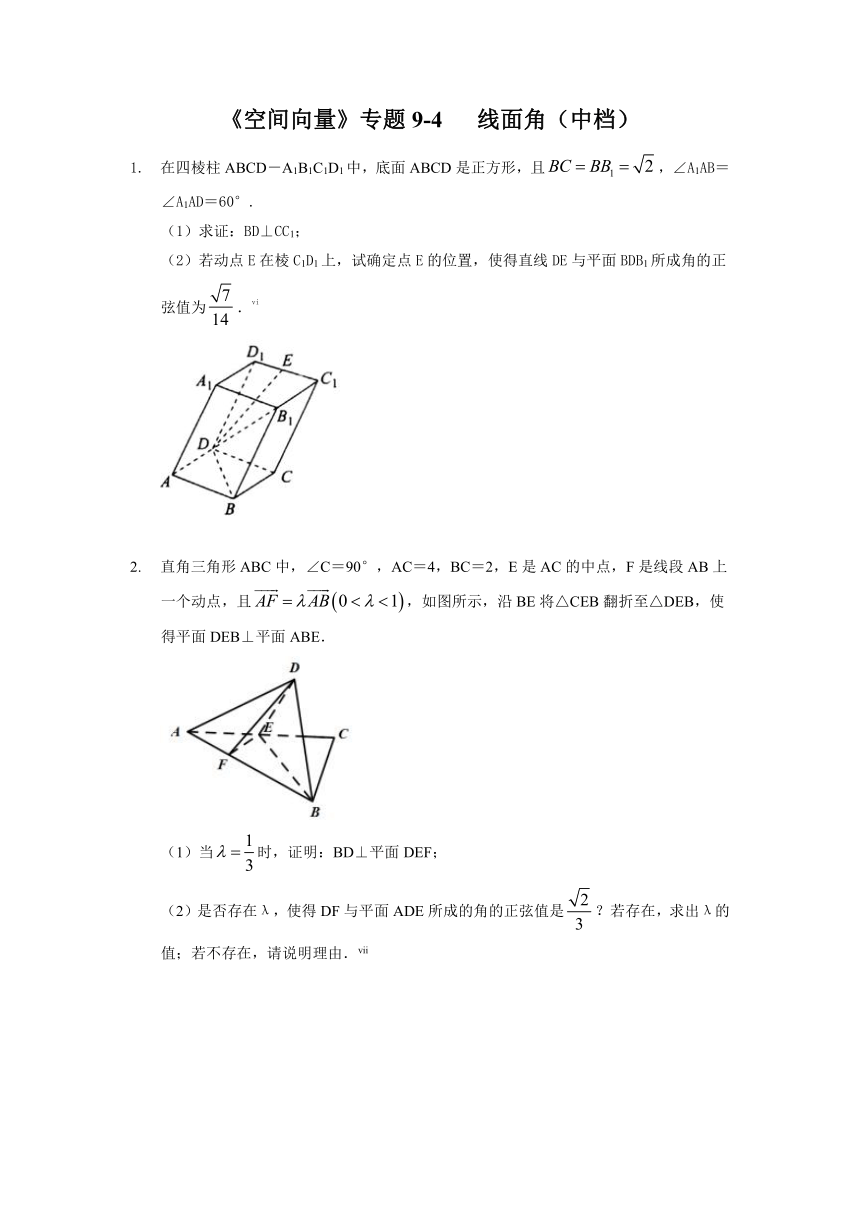
如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,
EF=AD=AB.
(1)过BD作截面与线段FC交于点N,使得AF∥平面BDN,试确定点N的位置,并予以证明;
(2)在(1)的条件下,求直线BN与平面ABF所成角的正弦值.[endnoteRef:3]
[3: 答案:N是CF的中点,;
解:(1)当N为CF的中点时,AF∥平面BDN.
证明:连结AC交BD于M,连结MN.
∵四边形ABCD是矩形,∴M是AC的中点,
∵N是CF的中点,
∴MN∥AF,又AF 平面BDN,MN 平面BDN,
∴AF∥平面BDN.
(2)过F作FO⊥平面ABCD,垂足为O,过O作x轴⊥AB,作y轴⊥BC于P,则P为BC的中点.
以O为原点,建立如图所示的空间直角坐标系,
设AD=1,则BF=1,FP=,∵EF==1,∴OP=(AB﹣EF)=,∴OF=.
∴A(,﹣,0),B(,,0),C(﹣,,0),F(0,0,),N(﹣,,).
∴=(0,2,0),=(﹣,,),=(﹣,﹣,).
设平面ABF的法向量为=(x,y,z),则,
∴,令z=得=(2,0,),
∴=﹣1,||=,||=.
∴cos<,>==﹣.
∴直线BN与平面ABF所成角的正弦值为|cos<,>|=.
]
如图1,在高为2的梯形ABCD中,AB//CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE-BCF,如图2.
(1)若AF⊥BD,证明:DE⊥BE;
(2)若DE//CF,,在线段AB上是否存在点P使得CP与平面ACD所成角的正弦值为?并说明理由.[endnoteRef:4]
[4: 答案:证明略,P为AB的中点;
证明:Ⅰ由已知得四边形ABEF是正方形,且边长为2,在图2中,,
由已知得平面BDE,
又平面,又平面ABEF,
又平面,
解:Ⅱ当P为AB的中点时满足条件在图2中,,即面DEFC,过E作交DC于点G,可知两两垂直,以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系分
则
设平面ACD的一个法向量为,则,
得分
设,则,可得.
设CP与平面ACD所成的角为,则
分,
所以P为AB的中点时满足条件分
Ⅰ由已知得四边形ABEF是正方形,且边长为2,取BE与AF的交点为O,推导出,从而平面BDE,进而,再由,得平面ABEF,从而,
Ⅱ以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系.
求得平面ACD的一个法向量为,设,则,可得.
设CP与平面ACD所成的角为,则,即可
本题考查了空间线线垂直,空间线面角,属于中档题.]
《空间向量》专题9-4 线面角(中档)
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,且,∠A1AB=∠A1AD=60°.
(1)求证:BD⊥CC1;
(2)若动点E在棱C1D1上,试确定点E的位置,使得直线DE与平面BDB1所成角的正弦值为.[endnoteRef:5]
[5: 答案:证明略,当为的中点时;
解:(1)连接,,,
因为,,
所以和均为正三角形,
于是.
设与的交点为,连接,则,
又四边形是正方形,所以,
而,所以平面,
又平面,所以,
又,所以.
(2)由,及,知,
于是,从而,
结合,,
得底面,
所以、、两两垂直.
如图,以点为坐标原点,的方向为轴的正方向,建立空间直角坐标系,
则,,,,,,,,
由,易求得.
设(),则,即.
设平面的一个法向量为,
由得令,得,
设直线与平面所成角为,则,
解得或(舍去).
所以当为的中点时,直线与平面所成角的正弦值为.
]
直角三角形ABC中,∠C=90°,AC=4,BC=2,E是AC的中点,F是线段AB上一个动点,且,如图所示,沿BE将△CEB翻折至△DEB,使得平面DEB⊥平面ABE.
(1)当时,证明:BD⊥平面DEF;
(2)是否存在λ,使得DF与平面ADE所成的角的正弦值是?若存在,求出λ的值;若不存在,请说明理由.[endnoteRef:6]
[6: 答案:证明略,;
证明:(1)在中,,即,则,
取的中点,连接交于,当时,是的中点,
而是的中点,所以是的中位线,所以,
在中,是的中点,所以是的中点,
在中,,
所以,则,
又平面平面,平面平面,
所以平面,
又平面,所以.
而,所以平面;
(2)以为原点,所在的直线为轴,所在的直线为轴,建立如图所示空间直角坐标系,则,
由(1)知是的中点,,又平面平面,
所以平面,则,
假设存在满足题意的,则由,
可得,
则,设平面的一个法向量为,
则即,
令,可得,即,
所以与平面所成的角的正弦值,
解得或3(舍去),
综上,存在,使得与平面所成的角的正弦值为.
]
(4套,4页,含答案)
如图(1),在边长为2的正方形ABCD中,E是边AB的中点.将△ADE沿DE折起,如图(2),F是折叠后AC的中点.
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若平面ADE⊥平面BCDE,求BF与平面ABD所成角的正弦值.[endnoteRef:0]
[0: 答案:证明略,;
【解析】(Ⅰ)取AD中点G,连结EG,FG,
∵F为AC中点, ∴FG綊CD,BE綊CD
∴FG綊BE,从而四边形EBFG是平行四边形.(3分)
∴BF∥EG,又BF?平面ADE,EG?平面ADE,
∴BF ∥平面ADE.(5分)
(Ⅱ) 如图所示以B为坐标原点,建立空间直角坐标系,在图(1)中作AH⊥DE于H,易求得EH=,AH=,
作HN⊥AE于N,HM⊥BC于M,则HN=,HM=,
所以A.(7分)
而B(0,0,0),D(2,2,0),则=,=(2,2,0).
设平面ABD的法向量为n=(x,y,z),
则?
解得一个法向量为n=(-,,-2).(9分)
又C(2,0,0),∴F,∴=,
∵cos〈n,〉==-.
∴BF与平面ABD所成角的正弦值为.(12分)
]
如图,在各棱长均为2的正三棱柱ABC-A1B1C1中,D,E分别为棱A1B1与BB1的中点,M,N为线段C1D上的动点,其中,M更靠近D,且MN=C1N.
(1)证明:A1E⊥平面AC1D;
(2)若NE与平面BCC1B1所成角的正弦值为,求异面直线BM与NE所成角的余弦值.[endnoteRef:1]
[1: 答案:证明略,;
(1)证明:由已知得为正三角形,为棱的中点,
∴,
在正三棱柱中,底面,则.
又,∴平面,∴.
易证,又,∴平面.
(2)解:取的中点,的中点,则,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,,,,
设,
则,
易知是平面的一个法向量,
∴,解得.
∴,,,,
∴,
∴异面直线与所成角的余弦值为.
]
《空间向量》专题9-2 线面角(中档)
如图(1)五边形ABCDE中,ED=EA,AB//CD,CD=2AB,∠EDC=150°,将△EAD沿AD折到△PAD的位置,得到四棱锥P-ABCD,如图(2),点M为线段PC的中点,且BM⊥平面PCD.
(1)求证:BM//平面PAD.
(2)若直线PC,AB与所成角的正切值为,求直线BM与平面PDB所成角的正弦值.[endnoteRef:2]
[2: 答案:证明略,;
(1)证明:取的中点,连接,则,
又,所以,………………………………2分
则四边形为平行四边形,所以,……………………………………3分
又因为面
所以平面……………………………………………………………………5分
(2)又平面,
∴平面,∴.
由即及为的中点,可得为等边三角形,
∴,又,∴,∴,
∴平面平面,
∴平面平面.………………………………………………………………6分
,∴为直线与所成的角,
由(1)可得,∴,∴,
设,则,
取的中点,连接,过作的平行线,
可建立如图所示的空间直角坐标系,
则,
∴,…………………………………………………………………9分
所以,
设为平面的法向量,则,即,
取,则为平面的一个法向量,
∵,
则直线与平面所成角的正弦值为.………………………………12分
]
如图四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是梯形,AB∥CD,BC⊥CD,AB=PD=4,CD=2,,M为CD的中点,N为PB上一点,且。
(1)若MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为,求异面直线AD与直线CN所成角的余弦值。
《空间向量》专题9-3 线面角(中档)
如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,
EF=AD=AB.
(1)过BD作截面与线段FC交于点N,使得AF∥平面BDN,试确定点N的位置,并予以证明;
(2)在(1)的条件下,求直线BN与平面ABF所成角的正弦值.[endnoteRef:3]
[3: 答案:N是CF的中点,;
解:(1)当N为CF的中点时,AF∥平面BDN.
证明:连结AC交BD于M,连结MN.
∵四边形ABCD是矩形,∴M是AC的中点,
∵N是CF的中点,
∴MN∥AF,又AF 平面BDN,MN 平面BDN,
∴AF∥平面BDN.
(2)过F作FO⊥平面ABCD,垂足为O,过O作x轴⊥AB,作y轴⊥BC于P,则P为BC的中点.
以O为原点,建立如图所示的空间直角坐标系,
设AD=1,则BF=1,FP=,∵EF==1,∴OP=(AB﹣EF)=,∴OF=.
∴A(,﹣,0),B(,,0),C(﹣,,0),F(0,0,),N(﹣,,).
∴=(0,2,0),=(﹣,,),=(﹣,﹣,).
设平面ABF的法向量为=(x,y,z),则,
∴,令z=得=(2,0,),
∴=﹣1,||=,||=.
∴cos<,>==﹣.
∴直线BN与平面ABF所成角的正弦值为|cos<,>|=.
]
如图1,在高为2的梯形ABCD中,AB//CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE-BCF,如图2.
(1)若AF⊥BD,证明:DE⊥BE;
(2)若DE//CF,,在线段AB上是否存在点P使得CP与平面ACD所成角的正弦值为?并说明理由.[endnoteRef:4]
[4: 答案:证明略,P为AB的中点;
证明:Ⅰ由已知得四边形ABEF是正方形,且边长为2,在图2中,,
由已知得平面BDE,
又平面,又平面ABEF,
又平面,
解:Ⅱ当P为AB的中点时满足条件在图2中,,即面DEFC,过E作交DC于点G,可知两两垂直,以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系分
则
设平面ACD的一个法向量为,则,
得分
设,则,可得.
设CP与平面ACD所成的角为,则
分,
所以P为AB的中点时满足条件分
Ⅰ由已知得四边形ABEF是正方形,且边长为2,取BE与AF的交点为O,推导出,从而平面BDE,进而,再由,得平面ABEF,从而,
Ⅱ以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系.
求得平面ACD的一个法向量为,设,则,可得.
设CP与平面ACD所成的角为,则,即可
本题考查了空间线线垂直,空间线面角,属于中档题.]
《空间向量》专题9-4 线面角(中档)
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,且,∠A1AB=∠A1AD=60°.
(1)求证:BD⊥CC1;
(2)若动点E在棱C1D1上,试确定点E的位置,使得直线DE与平面BDB1所成角的正弦值为.[endnoteRef:5]
[5: 答案:证明略,当为的中点时;
解:(1)连接,,,
因为,,
所以和均为正三角形,
于是.
设与的交点为,连接,则,
又四边形是正方形,所以,
而,所以平面,
又平面,所以,
又,所以.
(2)由,及,知,
于是,从而,
结合,,
得底面,
所以、、两两垂直.
如图,以点为坐标原点,的方向为轴的正方向,建立空间直角坐标系,
则,,,,,,,,
由,易求得.
设(),则,即.
设平面的一个法向量为,
由得令,得,
设直线与平面所成角为,则,
解得或(舍去).
所以当为的中点时,直线与平面所成角的正弦值为.
]
直角三角形ABC中,∠C=90°,AC=4,BC=2,E是AC的中点,F是线段AB上一个动点,且,如图所示,沿BE将△CEB翻折至△DEB,使得平面DEB⊥平面ABE.
(1)当时,证明:BD⊥平面DEF;
(2)是否存在λ,使得DF与平面ADE所成的角的正弦值是?若存在,求出λ的值;若不存在,请说明理由.[endnoteRef:6]
[6: 答案:证明略,;
证明:(1)在中,,即,则,
取的中点,连接交于,当时,是的中点,
而是的中点,所以是的中位线,所以,
在中,是的中点,所以是的中点,
在中,,
所以,则,
又平面平面,平面平面,
所以平面,
又平面,所以.
而,所以平面;
(2)以为原点,所在的直线为轴,所在的直线为轴,建立如图所示空间直角坐标系,则,
由(1)知是的中点,,又平面平面,
所以平面,则,
假设存在满足题意的,则由,
可得,
则,设平面的一个法向量为,
则即,
令,可得,即,
所以与平面所成的角的正弦值,
解得或3(舍去),
综上,存在,使得与平面所成的角的正弦值为.
]
