2021—2022学年苏科版数学七年级下册 7.4认识三角形 课件(共25张PPT)
文档属性
| 名称 | 2021—2022学年苏科版数学七年级下册 7.4认识三角形 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 08:06:21 | ||
图片预览







文档简介
(共25张PPT)
生活中的三角形
生活中的三角形
生活中的三角形
在我们的生活中,三角形随处可见。它简单,实用,可以帮助我们解决很多的实际问题。
问题情境
什么是三角形呢?
三角形:
揭示概念
由3条不在同一直线上的线段,首尾依次相接组成的图形。
怎样表示三角形呢?
揭示概念
A
B
C
三角形用符号“△”表示。
如左图,表示为:
△ABC
△ABC有:
(1)3个顶点:A、B、C;
(2)3条边:AB、BC、CA;
(3)3个角(内角):∠A、∠B、∠C.
a
b
c
特别地,△ABC的3条边也可用小写字母表示
为a、b、c.(大对小)
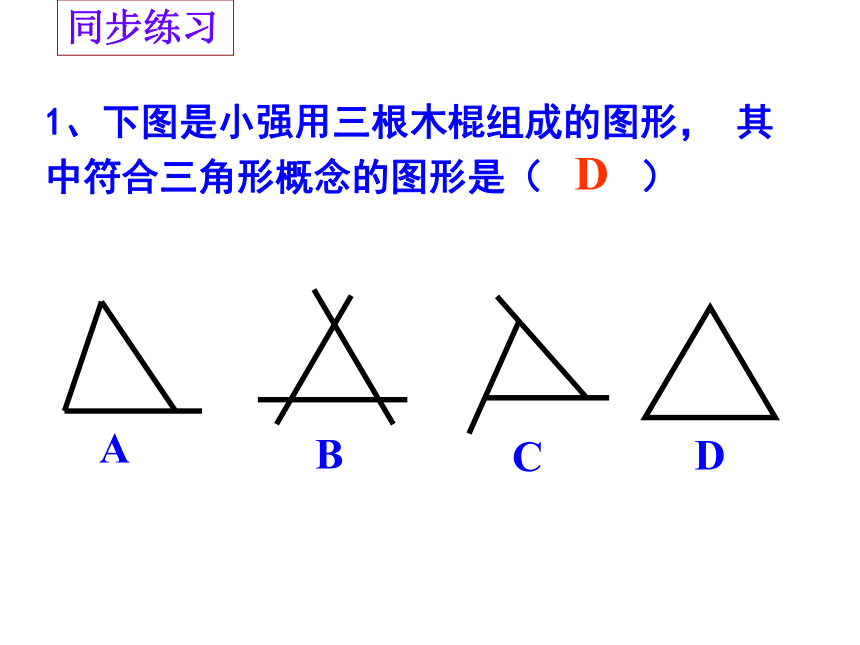
1、下图是小强用三根木棍组成的图形, 其中符合三角形概念的图形是( )
D
A
C
B
D
同步练习
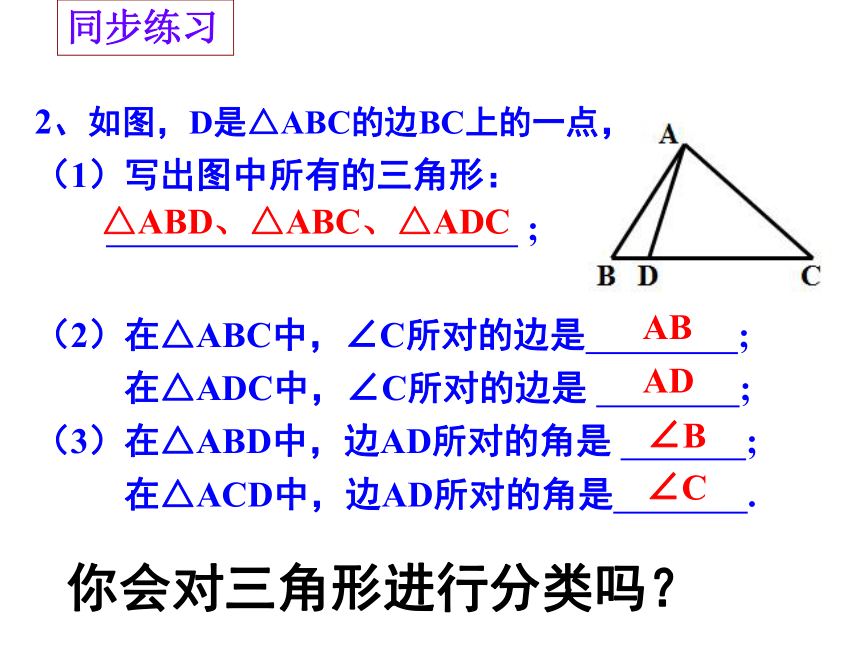
2、如图,D是△ABC的边BC上的一点,
(1)写出图中所有的三角形:
;
(2)在△ABC中,∠C所对的边是 ;
在△ADC中,∠C所对的边是 ;
(3)在△ABD中,边AD所对的角是 ;
在△ACD中,边AD所对的角是 .
同步练习
△ABD、△ABC、△ADC
AB
AD
∠B
∠C
你会对三角形进行分类吗?
锐角三角形
直角三角形
钝角三角形
①
②
③
④
⑤
⑥
做 一 做
三角形的分类:
归纳总结
锐角
直角
钝角
备注:
锐角三角形:3个角都是锐角的三角形;
直角三角形:有1个角是直角的三角形;
钝角三角形:有1个角是钝角的三角形.
这些三角形中, 还有等腰三角形吗
动手量一量。
做 一 做
① ② ⑤
三角形的分类:
归纳总结
等腰
备注:
等腰三角形:有2边相等的三角形;
等边三角形是特殊的等腰三角形,
即:腰和底相等的等腰三角形.
三角形的分类:
归纳总结
用符号表示图中的所有三角形,并把它们按角进行分类.
同步练习
锐角三角形:△ADE;
直角三角形:△ACD、△ACB;
钝角三角形:△ABD、△BDE.
探究新知
现有长度分别为1cm、2cm、3cm、4cm、5cm的线段. 从中抽取3条线段来画三角形。
1、若抽取5cm的线段作为一条边,则:另两边应如何抽取?填写下表:
×
三角形的两边之和大于第三边。
2、通过填表发现三角形三边有怎样的数量关系?
一条边
另两边
是?否?
3、4
5
5
5
5
5
5
2、4
2、3
1、4
1、3
1、2
×
×
×
√
√
探究新知
思考:三角形中,任意两边之和都大于第三边吗?
能根据“两点之间线段最短”来说明吗?
三角形的任意两边之和大于第三边。
∵BC是连接B、C两点的线段,
∴AB+AC>BC
(两点之间线段最短)
同理:AB+BC>AC
BC+AC>AB
它是判定能否构成三角形的重要依据。
例题解析
4 根小木棒的长度分别为2cm、3cm、4cm、5cm. 用其中3根搭三角形,可以搭出几个不同的三角形?
解:不同的组合有:
(1)2、3、4;
(2)2、3、5;
∵2+3=5
∴不能搭出三角形
(3)2、4、5;
(4)3、4、5.
∴ 可以搭出3个不同的三角形.
技巧:
只需比较较小的两边之和与最长边的大小即可.
同步练习
三条线段的长度分别为:
(1)8、10、3 ; (2)5、2、7 ;
(3)5、11、5 ; (4)20、12、13.
其中,能组成三角形的有( )组.
A、1 B、2 C、3 D、4
B
思维拓展
我们知道:
三角形的任意两边之和大于第三边.
那么:
三角形的任意两边之差 第三边.
<第三边< .
小于
两边之差
两边之和
1、若等腰三角形的两边长分别是4、10,
则它的周长是 .
思维拓展
2、若等腰△ABC的周长是16,AB=6,
则它的腰长是 .
24
6 或 5
思维拓展
3、有两根长度分别为 4 ㎝和 7 ㎝的木棒,
(1)第三边在什么范围内
(2)用长为 2㎝的木棒能与它们组成三角形吗
为什么
用长度为11㎝的木棒呢
(3)若第三边是奇数,则第三边可能是哪几个数
(4)若周长是奇数,则第三边可能是哪几个数
3cm<第三边<11cm
不能,因为2+4<7.
不能,因为4+7=11.
由(1)可知,第三边可能是5、7、9cm.
∵4+7=11,周长是奇数
∴第三边是偶数
由(1)可知,第三边可能是4、6、8、10cm.
全课总结
1. 三角形的概念、基本要素(顶点、边、角)、表示方法;
2. 三角形的分类(按角分类、按边分类);
3. 三角形的三边关系.
退出
生活中的三角形
生活中的三角形
生活中的三角形
在我们的生活中,三角形随处可见。它简单,实用,可以帮助我们解决很多的实际问题。
问题情境
什么是三角形呢?
三角形:
揭示概念
由3条不在同一直线上的线段,首尾依次相接组成的图形。
怎样表示三角形呢?
揭示概念
A
B
C
三角形用符号“△”表示。
如左图,表示为:
△ABC
△ABC有:
(1)3个顶点:A、B、C;
(2)3条边:AB、BC、CA;
(3)3个角(内角):∠A、∠B、∠C.
a
b
c
特别地,△ABC的3条边也可用小写字母表示
为a、b、c.(大对小)
1、下图是小强用三根木棍组成的图形, 其中符合三角形概念的图形是( )
D
A
C
B
D
同步练习
2、如图,D是△ABC的边BC上的一点,
(1)写出图中所有的三角形:
;
(2)在△ABC中,∠C所对的边是 ;
在△ADC中,∠C所对的边是 ;
(3)在△ABD中,边AD所对的角是 ;
在△ACD中,边AD所对的角是 .
同步练习
△ABD、△ABC、△ADC
AB
AD
∠B
∠C
你会对三角形进行分类吗?
锐角三角形
直角三角形
钝角三角形
①
②
③
④
⑤
⑥
做 一 做
三角形的分类:
归纳总结
锐角
直角
钝角
备注:
锐角三角形:3个角都是锐角的三角形;
直角三角形:有1个角是直角的三角形;
钝角三角形:有1个角是钝角的三角形.
这些三角形中, 还有等腰三角形吗
动手量一量。
做 一 做
① ② ⑤
三角形的分类:
归纳总结
等腰
备注:
等腰三角形:有2边相等的三角形;
等边三角形是特殊的等腰三角形,
即:腰和底相等的等腰三角形.
三角形的分类:
归纳总结
用符号表示图中的所有三角形,并把它们按角进行分类.
同步练习
锐角三角形:△ADE;
直角三角形:△ACD、△ACB;
钝角三角形:△ABD、△BDE.
探究新知
现有长度分别为1cm、2cm、3cm、4cm、5cm的线段. 从中抽取3条线段来画三角形。
1、若抽取5cm的线段作为一条边,则:另两边应如何抽取?填写下表:
×
三角形的两边之和大于第三边。
2、通过填表发现三角形三边有怎样的数量关系?
一条边
另两边
是?否?
3、4
5
5
5
5
5
5
2、4
2、3
1、4
1、3
1、2
×
×
×
√
√
探究新知
思考:三角形中,任意两边之和都大于第三边吗?
能根据“两点之间线段最短”来说明吗?
三角形的任意两边之和大于第三边。
∵BC是连接B、C两点的线段,
∴AB+AC>BC
(两点之间线段最短)
同理:AB+BC>AC
BC+AC>AB
它是判定能否构成三角形的重要依据。
例题解析
4 根小木棒的长度分别为2cm、3cm、4cm、5cm. 用其中3根搭三角形,可以搭出几个不同的三角形?
解:不同的组合有:
(1)2、3、4;
(2)2、3、5;
∵2+3=5
∴不能搭出三角形
(3)2、4、5;
(4)3、4、5.
∴ 可以搭出3个不同的三角形.
技巧:
只需比较较小的两边之和与最长边的大小即可.
同步练习
三条线段的长度分别为:
(1)8、10、3 ; (2)5、2、7 ;
(3)5、11、5 ; (4)20、12、13.
其中,能组成三角形的有( )组.
A、1 B、2 C、3 D、4
B
思维拓展
我们知道:
三角形的任意两边之和大于第三边.
那么:
三角形的任意两边之差 第三边.
<第三边< .
小于
两边之差
两边之和
1、若等腰三角形的两边长分别是4、10,
则它的周长是 .
思维拓展
2、若等腰△ABC的周长是16,AB=6,
则它的腰长是 .
24
6 或 5
思维拓展
3、有两根长度分别为 4 ㎝和 7 ㎝的木棒,
(1)第三边在什么范围内
(2)用长为 2㎝的木棒能与它们组成三角形吗
为什么
用长度为11㎝的木棒呢
(3)若第三边是奇数,则第三边可能是哪几个数
(4)若周长是奇数,则第三边可能是哪几个数
3cm<第三边<11cm
不能,因为2+4<7.
不能,因为4+7=11.
由(1)可知,第三边可能是5、7、9cm.
∵4+7=11,周长是奇数
∴第三边是偶数
由(1)可知,第三边可能是4、6、8、10cm.
全课总结
1. 三角形的概念、基本要素(顶点、边、角)、表示方法;
2. 三角形的分类(按角分类、按边分类);
3. 三角形的三边关系.
退出
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
