人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共17张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共17张PPT) | 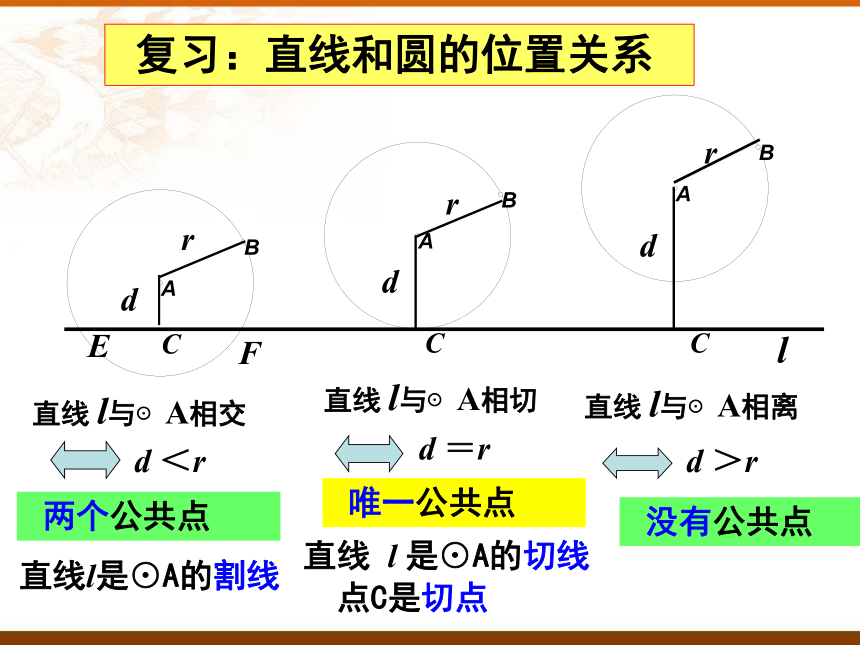 | |
| 格式 | zip | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 08:37:08 | ||
图片预览



文档简介
(共17张PPT)
复习:直线和圆的位置关系
l
d
d
d
C
C
C
E
F
r
r
r
直线 l与⊙A相交
d <r
直线 l与⊙A相切
d =r
直线 l与⊙A相离
d >r
直线l是⊙A的割线
直线 l 是⊙A的切线
两个公共点
唯一公共点
点C是切点
没有公共点
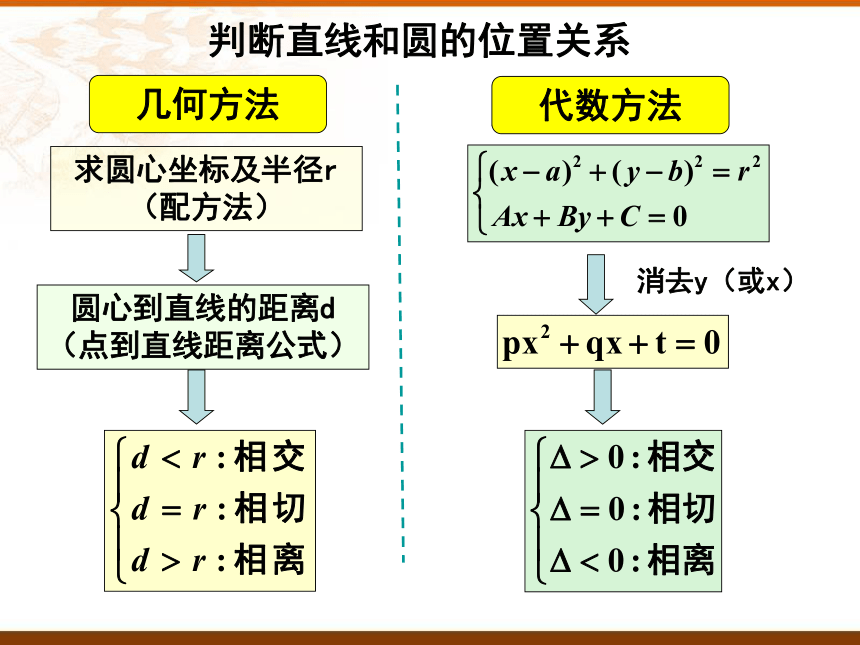
判断直线和圆的位置关系
几何方法
求圆心坐标及半径r(配方法)
圆心到直线的距离d (点到直线距离公式)
代数方法
消去y(或x)
§2.5.2 圆与圆的位置关系
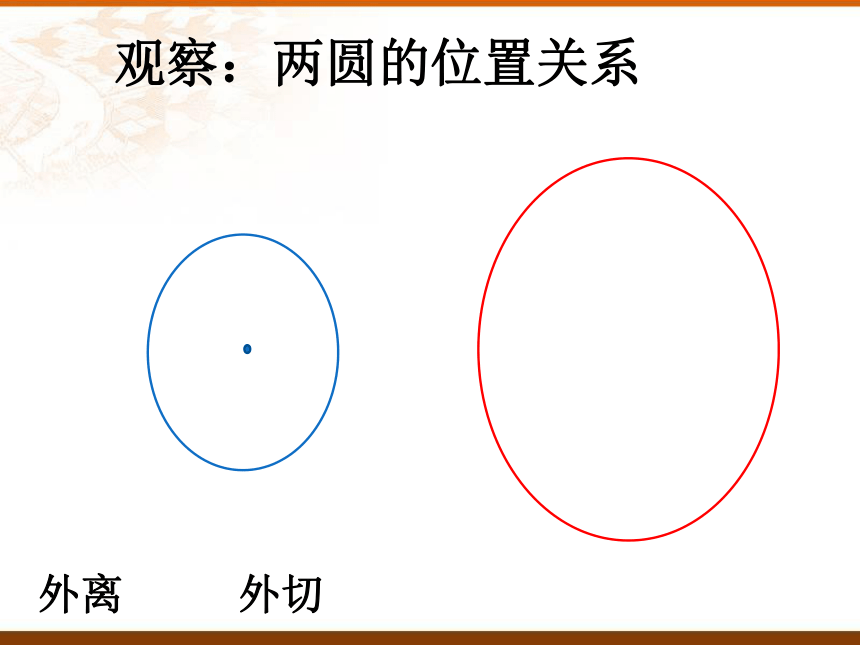
用你准备好的两个半径不同的圆,固定其中一张,而移动另一张,请观察圆与圆有几种位置关系?每种位置关系中两圆有多少公共点?
活动1:动手操作、观察猜想
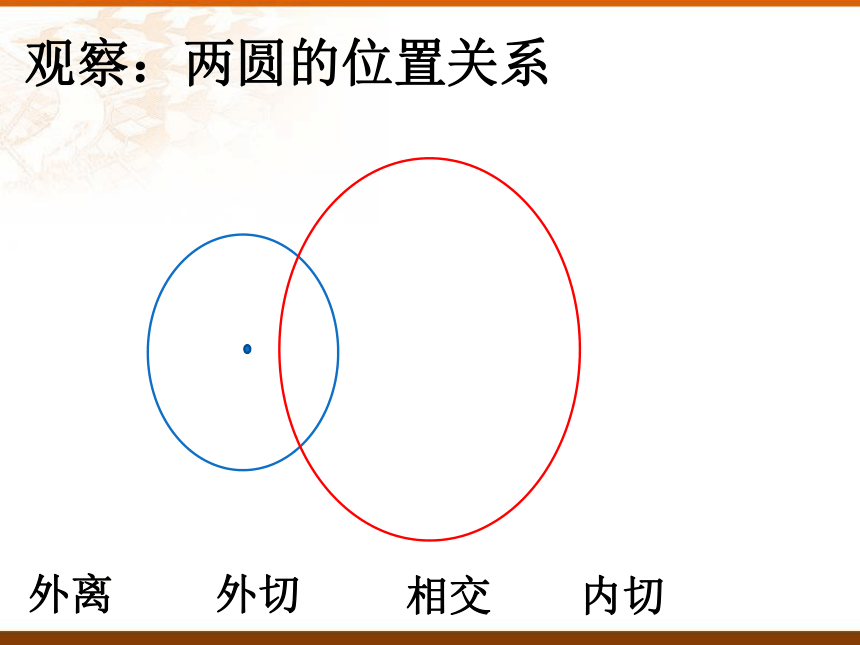
观察:两圆的位置关系
外离
外切
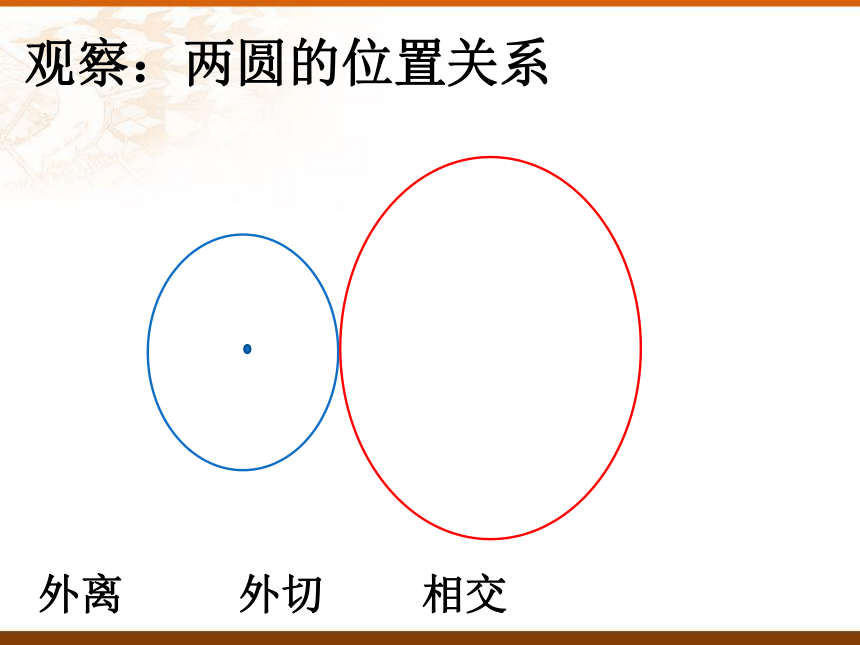
观察:两圆的位置关系
外离
外切
相交
观察:两圆的位置关系
外离
外切
相交
内切
观察:两圆的位置关系
外离
外切
相交
内切
内含
外离
|O1O2|>R+r
|O1O2|=R+r
|R-r|<|O1O2||O1O2|=|R-r|
0≤|O1O2|<|R-r|
|O1O2|=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
圆与圆的 位置关系:
五种
圆心距:|O1O2|
动画
判断两圆位置关系:
几何方法
求两圆的圆心坐标及半径(配方法)
求圆心距d
(两点间距离公式)
比较d和R,r的大小,下结论
外离:
d>R+r
d=R+r
|R-r|d=|R-r|
0≤d<|R-r|
外切:
相交:
内切:
内含:
结合图形记忆
圆心距:d
限时训练(5分钟):
判断C1和C2的位置关系
反思:
几何方法
求两圆的圆心坐标及半径(配方法)
求圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
代数方法
?
例5:已知圆C1:x2+y2+2x+8y-8=0和圆 C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
C1(-1,-4)
C2(2,2)
一、判断两圆位置关系
①
②
①-②化简得:x+2y-1=0
代入①化简得x2-2x-3=0
例5:已知圆C1:x2+y2+2x+8y-8=0和圆
C2:x2+y2-4x-4y-2=0,判断圆C1与圆C2的位置关系.
一、判断两圆位置关系
代数方法:
n=0
两个圆外离或内含
△<0
n=1
两个圆内切或外切
△=0
n=2
两个圆相交
△>0
消去y(或x)
几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0,Δ<0时,不能准确判断两圆的位置关系。
判断两圆的位置关系:
请看课本P98:练习1,2
例6:已知圆O的直径AB=4,动点M与点A的距离是它与点B的距离的 倍。试探究点M的轨迹,并判断该轨迹与圆O的位置关系。
解:以线段AB的中点O为原点,AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系由AB=4可得A(-2,0),B(2,0)
设点M(x,y)∵|MA|= |MB|
所以
化简得 ,即(x-6)2+y2=32
故点M的轨迹是以P(6,0)为圆心,半径为4的圆
因为圆心距|PO|=6,两圆半径r1=2,r2=4
又∵r2-r1<|PO|小结:判断两圆位置关系
几何方法
求两圆的圆心坐标及半径(配方法)
求圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
代数方法
消去y(或x)
请看课本P98:习题2.5 第5,9题
复习:直线和圆的位置关系
l
d
d
d
C
C
C
E
F
r
r
r
直线 l与⊙A相交
d <r
直线 l与⊙A相切
d =r
直线 l与⊙A相离
d >r
直线l是⊙A的割线
直线 l 是⊙A的切线
两个公共点
唯一公共点
点C是切点
没有公共点
判断直线和圆的位置关系
几何方法
求圆心坐标及半径r(配方法)
圆心到直线的距离d (点到直线距离公式)
代数方法
消去y(或x)
§2.5.2 圆与圆的位置关系
用你准备好的两个半径不同的圆,固定其中一张,而移动另一张,请观察圆与圆有几种位置关系?每种位置关系中两圆有多少公共点?
活动1:动手操作、观察猜想
观察:两圆的位置关系
外离
外切
观察:两圆的位置关系
外离
外切
相交
观察:两圆的位置关系
外离
外切
相交
内切
观察:两圆的位置关系
外离
外切
相交
内切
内含
外离
|O1O2|>R+r
|O1O2|=R+r
|R-r|<|O1O2|
0≤|O1O2|<|R-r|
|O1O2|=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
r
R
O1
O2
圆与圆的 位置关系:
五种
圆心距:|O1O2|
动画
判断两圆位置关系:
几何方法
求两圆的圆心坐标及半径(配方法)
求圆心距d
(两点间距离公式)
比较d和R,r的大小,下结论
外离:
d>R+r
d=R+r
|R-r|
0≤d<|R-r|
外切:
相交:
内切:
内含:
结合图形记忆
圆心距:d
限时训练(5分钟):
判断C1和C2的位置关系
反思:
几何方法
求两圆的圆心坐标及半径(配方法)
求圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
代数方法
?
例5:已知圆C1:x2+y2+2x+8y-8=0和圆 C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
C1(-1,-4)
C2(2,2)
一、判断两圆位置关系
①
②
①-②化简得:x+2y-1=0
代入①化简得x2-2x-3=0
例5:已知圆C1:x2+y2+2x+8y-8=0和圆
C2:x2+y2-4x-4y-2=0,判断圆C1与圆C2的位置关系.
一、判断两圆位置关系
代数方法:
n=0
两个圆外离或内含
△<0
n=1
两个圆内切或外切
△=0
n=2
两个圆相交
△>0
消去y(或x)
几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0,Δ<0时,不能准确判断两圆的位置关系。
判断两圆的位置关系:
请看课本P98:练习1,2
例6:已知圆O的直径AB=4,动点M与点A的距离是它与点B的距离的 倍。试探究点M的轨迹,并判断该轨迹与圆O的位置关系。
解:以线段AB的中点O为原点,AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系由AB=4可得A(-2,0),B(2,0)
设点M(x,y)∵|MA|= |MB|
所以
化简得 ,即(x-6)2+y2=32
故点M的轨迹是以P(6,0)为圆心,半径为4的圆
因为圆心距|PO|=6,两圆半径r1=2,r2=4
又∵r2-r1<|PO|
几何方法
求两圆的圆心坐标及半径(配方法)
求圆心距d
(两点间距离公式)
比较d和r1,r2的大小,下结论
代数方法
消去y(或x)
请看课本P98:习题2.5 第5,9题
