人教B版(2019)选择性必修第一册2.3.1圆的标准方程 2.3.2圆的一般方程 课件(共38张PPT)
文档属性
| 名称 | 人教B版(2019)选择性必修第一册2.3.1圆的标准方程 2.3.2圆的一般方程 课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
2.3 圆及其方程
2.3.1 圆的标准方程
2.3.2 圆的一般方程
第二章 平面解析几何
重点:圆的标准方程以及根据已知条件求圆的标准方程
难点:圆的标准方程以及根据已知条件求圆的标准方程
1.会用定义推导圆的标准方程并掌握圆的标准方程的特征.
2.能根据所给条件求圆的标准方程.
3.掌握点与圆的位置关系.
学习目标
1.圆的标准方程
一般地,如果平面直角坐标系中⊙C的圆心为C(a,b),半径为r(r>0),设M(x,y)为平面直角坐标系中任意一点,则点M在⊙C上的充要条件是|CM|=r,即=r,两边平方,得
(x-a)2+(y-b)2=r2.
此方程表示以点 为圆心, 为半径的圆,通常称为圆的标准方程.
C(a,b)
r
2.点与圆的位置关系
点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
点M在圆外(x0-a)2+(y0-b)2>r2;
点M在圆上(x0-a)2+(y0-b)2=r2;
点M在圆内(x0-a)2+(y0-b)23. 圆的一般方程
一般地,形式x2+y2+Dx+Ey+F=0,其中D,E,F都是常数.称为圆的一般方程.
(1)当 >0时,方程是以为圆心,为半径的圆的方程;
(2)当D2+E2-4F=0时,满足方程的实数只有x=-,y=-,所以原方程不是
圆的方程;
(3)当D2+E2-4F<0时,方程没有实数解,因而原方程也不是圆的方程.
一 圆的标准方程
<1>辨析圆的标准方程
例1 圆(x-1)2+(y+2)2=4的圆心坐标和半径分别为 ( )
A.(1,-2),4 B.(1,2),4
C.(1,-2),2 D.(1,2),2
【解析】 圆(x-1)2+(y+2)2=4的圆心坐标为(1,-2),半径r=2.
【答案】 C
若点P(-1,)在圆x2+y2=m2上,则实数m= .
解析:把P(-1, )代入x2+y2=m2,得1+3=m2,∴ m=2或-2.
<2>求圆的标准方程
例2 圆心为C(2,-3),且经过坐标原点的圆的标准方程为 .
【解析】 (方法1)由题意可设圆的方程为(x-2)2+(y+3)2=r2(r>0),因为坐标原点在圆上,所以r2=13,故圆的标准方程为(x-2)2+(y+3)2=13.
(方法2)由题意可知圆的半径为原点O与点C(2,-3)间的距离,则r==,所以圆的标准方程为(x-2)2+(y+3)2=13.
【答案】 (x-2)2+(y+3)2=13
1.[2020·江苏苏州高二检测]在平面直角坐标系xOy中,A(-2,0),B(2,2),则以线段AB为直径的圆的标准方程为 .
解析:(方法1)∵ A(-2,0),B(2,2),
∴ 以线段AB为直径的圆的圆心为C(0,1),
半径为r=|AB|==,
∴ 所求圆的标准方程为x2+(y-1)2=5.
(方法2)以线段AB为直径的圆的方程为(x+2)(x-2)+y(y-2)=0,即x2+y2-2y-4=0,∴ 所求圆的标准方程为x2+(y-1)2=5.
2. [2020·四川绵阳南山中学高二检测]圆(x+2)2+y2=5关于y轴对称的圆的方程为( )
A.(x-2)2+y2=5 B.x2+(y-2)2=5
C.(x+2)2+(y+2)2=5 D.x2+(y+2)2=5
解析:圆心(-2,0)关于y轴的对称点为(2,0),
所以所求圆的方程为(x-2)2+y2=5.
求圆的标准方程的方法
1.待定系数法(代数法)
根据条件设出圆的标准方程(x-a)2+(y-b)2=r2, 再由题目给出的条件,列出关于a,b,r的方程组,求出a,b,r代入标准方程.
2.直接法(几何法)
根据圆的几何性质,直接求得圆心坐标和半径.常用到的几何性质有:①圆心在过切点且与切线垂直的直线上;②圆心到切线的距离等于半径;③圆心在圆的任意弦的中垂线上,且弦长的一半、弦心距d、半径r满足r2=d2+;
④两圆相切时,切点与两圆心三点共线等.
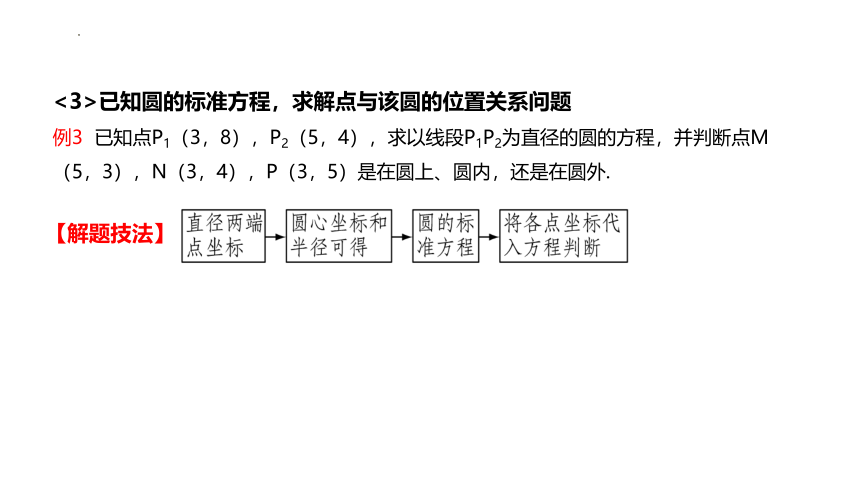
<3>已知圆的标准方程,求解点与该圆的位置关系问题
例3 已知点P1(3,8),P2(5,4),求以线段P1P2为直径的圆的方程,并判断点M(5,3),N(3,4),P(3,5)是在圆上、圆内,还是在圆外.
【解题技法】
【解】 设圆心C(a,b),半径为r,则由C为线段P1P2的中点得a==4,b==6,即圆心坐标为C(4,6).
又由两点间的距离公式得r=CP1==,
故所求圆的标准方程为(x-4)2+(y-6)2=5.
(方法1)分别计算点M,N,P到圆心C的距离:CM= =>,CN= =,CP= =<,所以点M在圆外,点N在圆上,点P在圆内.
(方法2)由于(5-4)2+(3-6)2=10>5,故点M在圆外;
由于(3-4)2+(4-6)2=5,故点N在圆上;
由于(3-4)2+(5-6)2=2<5,故点P在圆内.
例4 已知圆C的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求半径a;
(2)若点P(3,3)与Q(5,3)有一点在圆内,另一点在圆外,求a的取值范围.
【解题提示】 (1)由点在圆上,满足圆的方程可求得a的值;(2)点在圆内(外),则点与圆心的距离小于(大于)圆的半径,可求a的范围.
【解】 (1)∵ 点M(6,9)在圆上,
∴ (6-5)2+(9-6)2=a2,即a2=10.
又a>0,∴ a=.
(2)易知圆心C的坐标为(5,6),
∴ PC==,
QC==3,且PC>QC,
∴ 点P在圆外,点Q在圆内,∴ 3(1)已知点P(1,1)在圆(x-a)2+(y+a)2=4的内部,求实数a的取值范围.
(2)已知点A(1,2)在圆C:(x+a)2+(y-a)2=2a2的外部,求实数a的取值范围.
解:(1)∵ 点P(1,1)在圆(x-a)2+(y+a)2=4的内部,
∴ (1-a)2+(1+a)2<4,即a2<1.解得-1(2)∵ 点A(1,2)在圆C的外部,∴ (1+a)2+(2-a)2>2a2,即5-2a>0,
∴ a<.又2a2>0,∴ a≠0,∴ a的取值范围是a|a<且a≠0}.
二 圆的一般方程
<1>二元二次方程表示圆的条件
例4 若方程a2x2+(a+2)y2+2ax+a=0表示圆,则a的值为 ( )
A.1或-2 B.2或-1 C.-1 D.2
【解析】 若方程a2x2+(a+2)y2+2ax+a=0表示圆,
则解得a=-1.
【答案】 C
1.[2020·四川蓉城名校联盟高二检测]若方程x2+y2-2tx+4y+2t+7=0表示圆,则实数t的取值范围是 .
解析:若方程x2+y2-2tx+4y+2t+7=0表示圆,则(-2t)2+42-4(2t+7)>0,解得t<-1或t>3.
(-∞,-1)∪(3,+∞)
解析:若方程x2+y2-ax+2y+1=0能表示圆,则(-a)2+22-4×1>0,解得a≠0.所以,若方程x2+y2-ax+2y+1=0不能表示圆,则a=0.
2.[2020·山东青岛高二检测]若方程x2+y2-ax+2y+1=0不能表示圆,则实数a的值为( )
A.0 B.1 C.-1 D.2
A
<2>圆的一般方程与标准方程的互化
例5 已知圆C:x2+y2+Dx+Ey+=0的圆心坐标是,则此圆的半径为( )
A.2 B.3 C.4 D.5
【解析】圆C:x2+y2+Dx+Ey+=0,即+= ,表示以点 为圆心,半径为的圆.根据圆C的圆心坐标是,得D=1,E=-4,故圆C的半径为=2.
【答案】 A
[2020·湖北华中师大一附中高二检测]圆C:2x2+2y2+ax-4y-3=0的直径为,则圆C的圆心坐标可能是 ( )
A. B. C.(3,2) D.(-3,2)
解析:圆C的标准方程为+(y-1)2=+,故+=,所以=,解得a=±6,所以圆C的圆心坐标为.
A
<3>求圆的一般方程
例6 已知△ABC的顶点坐标为A(1,1),B(2,4),直线l经过点B且与直线x-y+1=0平行,点A和点C关于直线l对称.
(1)求直线AC的方程;(2)求△ABC外接圆的方程.
【解题提示】 (1)先由题意求出直线l的方程,再由点A和点C关于直线l对称,确定直线AC的斜率,由点斜式写出直线AC的方程即可;(2)可根据题意求出圆心坐标以及半径,得到圆的标准方程;也可结合(1)的结果先求出点C的坐标,再由待定系数法设出圆的一般方程,将A、B、C三点坐标代入得出方程组,求解即可.
【解】 (1)∵ 直线l与直线x-y+1=0平行,∴ 直线l的斜率kl=1.
又∵ 点A和点C关于直线l对称,
∴ 直线AC与l垂直,∴ 直线AC的斜率kAC=-1.
又∵ 直线AC过点A(1,1),∴ 直线AC的方程为y-1=-(x-1),
即x+y-2=0.
(2)(方法1)∵ kl=1且直线l经过点B(2,4)
∴ 直线l的方程为y-4=x-2,即x-y+2=0.∵ A(1,1),B(2,4),
∴ AB的中点为,直线AB的斜率kAB==3,
∴ 线段AB的垂直平分线的方程为y-=-,即x+3y-9=0.
△ABC的外接圆的圆心即为直线l与x+3y-9=0的交点.
由得∴ △ABC外接圆的圆心坐标为,
∴ 半径r==,∴ △ABC外接圆的方程为+=.
(方法2)设直线l的方程为x-y+c=0,∵ 直线l经过点B(2,4),
∴ 2-4+c=0,∴ c=2,即直线l的方程为x-y+2=0.
设C(x0,y0),由(1)知kAC=-1,即=-1.①
又∵ 线段AC的中点在直线l上,∴-+2=0.②
由①②得x0=-1,y0=3,∴ C(-1,3).
设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,
由题意可得解得
故△ABC外接圆的方程为x2+y2-x-y+5=0.
[2020·河南驻马店高一期末]已知△ABC三个顶点坐标为A(0,2),B(0,-2),C(-2,2).
(1)在△ABC中,求与BC边平行的中位线所在直线的方程;
(2)求△ABC外接圆的方程.
解:(1)由题意知,AC边的中点为(-1,2),AB边的中点为(0,0),
故与BC边平行的中位线所在直线方程为2x+y=0.
(2)设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,
把A,B,C三点的坐标代入外接圆的方程,得
解得
故所求的圆的方程为x2+y2+2x-4=0.
过不共线的三点A,B,C的圆的方程的求法
1.待定系数法(代数法):设出圆的一般方程x2+y2+Dx+Ey+F=0,分别把三个点的坐标代入,求出待定系数D,E,F,即可求出圆的方程;
2.直接法(几何法):因为所求圆为△ABC的外接圆,所以△ABC任意两边的中垂线交点即为外接圆的圆心,顶点到圆心的距离即为外接圆的半径,代入圆的标准方程即可.
<4>点与圆的位置关系问题
例7 已知点A是圆C:x2+y2+ax+4y-5=0上任意一点,点A关于直线x+2y-1=0的对称点也在此圆上,则实数a= .
【解析】 由题意可知,圆C的圆心在直线x+2y-1=0上,则--4-1=0,解得a=-10.
【答案】 -10
[2020·浙江湖州高一检测]过点P(-3,0)作直线:2x+(λ+1)y+2λ=0(λ∈R)的垂线,垂足为M,已知点N(3,2),则当λ变化时,|MN|的取值范围是( )
A.[0,5+] B.[5- ,5+ ]
C.[5,5+ ] D.[5- ,5]
B
解析:直线2x+(λ+1)y+2λ=0(λ∈R),
即(2x+y)+λ(y+2)=0.
由得直线经过定点Q(1,-2).
由△PQM为直角三角形,斜边为PQ,M在以PQ为直径的圆上运动,
可得圆心为PQ的中点H(-1,-1),半径r=|PQ|=,
则|MN|的最大值为|NH|+r=+=5+;
|MN|的最小值为|NH|-r= -=5-.
故|MN|的取值范围为[5- ,5+ ].
题组三 与圆有关的轨迹问题
例8 已知点A(-2,0),B(2,0),动点P满足|PA|=λ|PB|(λ>0),若点P的轨迹为一条直线,则λ= ;若λ=2,则点P的轨迹方程为 .
【解题提示】 设P(x,y),把|PA|=λ|PB|两边平方,整理得,
(1-λ2)x2+(1-λ2)y2+4(1+λ2)x+4-4λ2=0,从而可得结果.
【解析】 设P(x,y),由|PA|=λ|PB|可得,=,
两边平方,整理得点P的轨迹方程为
(1-λ2)x2+(1-λ2)y2+4(1+λ2)x+4-4λ2=0.
若该方程表示直线,则解得λ=1.
当λ=2时,点P的轨迹方程为3x2+3y2-20x+12=0,
即x2+y2-x+4=0.
【答案】 1;x2+y2-x+4=0
已知圆C与y轴相切,圆心在直线x-2y=0上,且经过点A(2,3),求圆C的方程.
解:∵ 圆心在直线x-2y=0上,∴ 设圆心坐标为(2a,a).
又圆C与y轴相切,∴ 半径r=2|a|.
设圆C的标准方程为(x-2a)2+(y-a)2=4a2,
∵ 圆C经过点A(2,3),∴ (2-2a)2+(3-a)2=4a2,∴ a=1或a=13,
∴ 圆C的方程为(x-2)2+(y-1)2=4或(x-26)2+(y-13)2=676.
求轨迹方程的常用方法
1.直接法:直接利用条件建立x,y之间的关系F(x,y)=0.
2.定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义写出动点的轨迹方程.
3.代入(相关点)法:动点P(x,y)随另一动点Q(x0,y0)的变化而变化,常利用代入法求动点P(x,y)的轨迹方程.
小结
1.圆的标准方程
圆的标准方程:(x-a)2+(y-b)2=r2.
表示以点(a,b)为圆心,r为半径的圆.
2.点与圆的位置关系
点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
点M在圆外(x0-a)2+(y0-b)2>r2;
点M在圆上(x0-a)2+(y0-b)2=r2;
点M在圆内(x0-a)2+(y0-b)23. 圆的一般方程
一般地,形式x2+y2+Dx+Ey+F=0,其中D,E,F都是常数.称为圆的一般方程.
(1)当 >0时,方程是以为圆心,为半径的圆的方程;
(2)当D2+E2-4F=0时,满足方程的实数只有x=-,y=-,所以原方程不是
圆的方程;
(3)当D2+E2-4F<0时,方程没有实数解,因而原方程也不是圆的方程.
2.3 圆及其方程
2.3.1 圆的标准方程
2.3.2 圆的一般方程
第二章 平面解析几何
重点:圆的标准方程以及根据已知条件求圆的标准方程
难点:圆的标准方程以及根据已知条件求圆的标准方程
1.会用定义推导圆的标准方程并掌握圆的标准方程的特征.
2.能根据所给条件求圆的标准方程.
3.掌握点与圆的位置关系.
学习目标
1.圆的标准方程
一般地,如果平面直角坐标系中⊙C的圆心为C(a,b),半径为r(r>0),设M(x,y)为平面直角坐标系中任意一点,则点M在⊙C上的充要条件是|CM|=r,即=r,两边平方,得
(x-a)2+(y-b)2=r2.
此方程表示以点 为圆心, 为半径的圆,通常称为圆的标准方程.
C(a,b)
r
2.点与圆的位置关系
点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
点M在圆外(x0-a)2+(y0-b)2>r2;
点M在圆上(x0-a)2+(y0-b)2=r2;
点M在圆内(x0-a)2+(y0-b)2
一般地,形式x2+y2+Dx+Ey+F=0,其中D,E,F都是常数.称为圆的一般方程.
(1)当 >0时,方程是以为圆心,为半径的圆的方程;
(2)当D2+E2-4F=0时,满足方程的实数只有x=-,y=-,所以原方程不是
圆的方程;
(3)当D2+E2-4F<0时,方程没有实数解,因而原方程也不是圆的方程.
一 圆的标准方程
<1>辨析圆的标准方程
例1 圆(x-1)2+(y+2)2=4的圆心坐标和半径分别为 ( )
A.(1,-2),4 B.(1,2),4
C.(1,-2),2 D.(1,2),2
【解析】 圆(x-1)2+(y+2)2=4的圆心坐标为(1,-2),半径r=2.
【答案】 C
若点P(-1,)在圆x2+y2=m2上,则实数m= .
解析:把P(-1, )代入x2+y2=m2,得1+3=m2,∴ m=2或-2.
<2>求圆的标准方程
例2 圆心为C(2,-3),且经过坐标原点的圆的标准方程为 .
【解析】 (方法1)由题意可设圆的方程为(x-2)2+(y+3)2=r2(r>0),因为坐标原点在圆上,所以r2=13,故圆的标准方程为(x-2)2+(y+3)2=13.
(方法2)由题意可知圆的半径为原点O与点C(2,-3)间的距离,则r==,所以圆的标准方程为(x-2)2+(y+3)2=13.
【答案】 (x-2)2+(y+3)2=13
1.[2020·江苏苏州高二检测]在平面直角坐标系xOy中,A(-2,0),B(2,2),则以线段AB为直径的圆的标准方程为 .
解析:(方法1)∵ A(-2,0),B(2,2),
∴ 以线段AB为直径的圆的圆心为C(0,1),
半径为r=|AB|==,
∴ 所求圆的标准方程为x2+(y-1)2=5.
(方法2)以线段AB为直径的圆的方程为(x+2)(x-2)+y(y-2)=0,即x2+y2-2y-4=0,∴ 所求圆的标准方程为x2+(y-1)2=5.
2. [2020·四川绵阳南山中学高二检测]圆(x+2)2+y2=5关于y轴对称的圆的方程为( )
A.(x-2)2+y2=5 B.x2+(y-2)2=5
C.(x+2)2+(y+2)2=5 D.x2+(y+2)2=5
解析:圆心(-2,0)关于y轴的对称点为(2,0),
所以所求圆的方程为(x-2)2+y2=5.
求圆的标准方程的方法
1.待定系数法(代数法)
根据条件设出圆的标准方程(x-a)2+(y-b)2=r2, 再由题目给出的条件,列出关于a,b,r的方程组,求出a,b,r代入标准方程.
2.直接法(几何法)
根据圆的几何性质,直接求得圆心坐标和半径.常用到的几何性质有:①圆心在过切点且与切线垂直的直线上;②圆心到切线的距离等于半径;③圆心在圆的任意弦的中垂线上,且弦长的一半、弦心距d、半径r满足r2=d2+;
④两圆相切时,切点与两圆心三点共线等.
<3>已知圆的标准方程,求解点与该圆的位置关系问题
例3 已知点P1(3,8),P2(5,4),求以线段P1P2为直径的圆的方程,并判断点M(5,3),N(3,4),P(3,5)是在圆上、圆内,还是在圆外.
【解题技法】
【解】 设圆心C(a,b),半径为r,则由C为线段P1P2的中点得a==4,b==6,即圆心坐标为C(4,6).
又由两点间的距离公式得r=CP1==,
故所求圆的标准方程为(x-4)2+(y-6)2=5.
(方法1)分别计算点M,N,P到圆心C的距离:CM= =>,CN= =,CP= =<,所以点M在圆外,点N在圆上,点P在圆内.
(方法2)由于(5-4)2+(3-6)2=10>5,故点M在圆外;
由于(3-4)2+(4-6)2=5,故点N在圆上;
由于(3-4)2+(5-6)2=2<5,故点P在圆内.
例4 已知圆C的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求半径a;
(2)若点P(3,3)与Q(5,3)有一点在圆内,另一点在圆外,求a的取值范围.
【解题提示】 (1)由点在圆上,满足圆的方程可求得a的值;(2)点在圆内(外),则点与圆心的距离小于(大于)圆的半径,可求a的范围.
【解】 (1)∵ 点M(6,9)在圆上,
∴ (6-5)2+(9-6)2=a2,即a2=10.
又a>0,∴ a=.
(2)易知圆心C的坐标为(5,6),
∴ PC==,
QC==3,且PC>QC,
∴ 点P在圆外,点Q在圆内,∴ 3
(2)已知点A(1,2)在圆C:(x+a)2+(y-a)2=2a2的外部,求实数a的取值范围.
解:(1)∵ 点P(1,1)在圆(x-a)2+(y+a)2=4的内部,
∴ (1-a)2+(1+a)2<4,即a2<1.解得-1
∴ a<.又2a2>0,∴ a≠0,∴ a的取值范围是a|a<且a≠0}.
二 圆的一般方程
<1>二元二次方程表示圆的条件
例4 若方程a2x2+(a+2)y2+2ax+a=0表示圆,则a的值为 ( )
A.1或-2 B.2或-1 C.-1 D.2
【解析】 若方程a2x2+(a+2)y2+2ax+a=0表示圆,
则解得a=-1.
【答案】 C
1.[2020·四川蓉城名校联盟高二检测]若方程x2+y2-2tx+4y+2t+7=0表示圆,则实数t的取值范围是 .
解析:若方程x2+y2-2tx+4y+2t+7=0表示圆,则(-2t)2+42-4(2t+7)>0,解得t<-1或t>3.
(-∞,-1)∪(3,+∞)
解析:若方程x2+y2-ax+2y+1=0能表示圆,则(-a)2+22-4×1>0,解得a≠0.所以,若方程x2+y2-ax+2y+1=0不能表示圆,则a=0.
2.[2020·山东青岛高二检测]若方程x2+y2-ax+2y+1=0不能表示圆,则实数a的值为( )
A.0 B.1 C.-1 D.2
A
<2>圆的一般方程与标准方程的互化
例5 已知圆C:x2+y2+Dx+Ey+=0的圆心坐标是,则此圆的半径为( )
A.2 B.3 C.4 D.5
【解析】圆C:x2+y2+Dx+Ey+=0,即+= ,表示以点 为圆心,半径为的圆.根据圆C的圆心坐标是,得D=1,E=-4,故圆C的半径为=2.
【答案】 A
[2020·湖北华中师大一附中高二检测]圆C:2x2+2y2+ax-4y-3=0的直径为,则圆C的圆心坐标可能是 ( )
A. B. C.(3,2) D.(-3,2)
解析:圆C的标准方程为+(y-1)2=+,故+=,所以=,解得a=±6,所以圆C的圆心坐标为.
A
<3>求圆的一般方程
例6 已知△ABC的顶点坐标为A(1,1),B(2,4),直线l经过点B且与直线x-y+1=0平行,点A和点C关于直线l对称.
(1)求直线AC的方程;(2)求△ABC外接圆的方程.
【解题提示】 (1)先由题意求出直线l的方程,再由点A和点C关于直线l对称,确定直线AC的斜率,由点斜式写出直线AC的方程即可;(2)可根据题意求出圆心坐标以及半径,得到圆的标准方程;也可结合(1)的结果先求出点C的坐标,再由待定系数法设出圆的一般方程,将A、B、C三点坐标代入得出方程组,求解即可.
【解】 (1)∵ 直线l与直线x-y+1=0平行,∴ 直线l的斜率kl=1.
又∵ 点A和点C关于直线l对称,
∴ 直线AC与l垂直,∴ 直线AC的斜率kAC=-1.
又∵ 直线AC过点A(1,1),∴ 直线AC的方程为y-1=-(x-1),
即x+y-2=0.
(2)(方法1)∵ kl=1且直线l经过点B(2,4)
∴ 直线l的方程为y-4=x-2,即x-y+2=0.∵ A(1,1),B(2,4),
∴ AB的中点为,直线AB的斜率kAB==3,
∴ 线段AB的垂直平分线的方程为y-=-,即x+3y-9=0.
△ABC的外接圆的圆心即为直线l与x+3y-9=0的交点.
由得∴ △ABC外接圆的圆心坐标为,
∴ 半径r==,∴ △ABC外接圆的方程为+=.
(方法2)设直线l的方程为x-y+c=0,∵ 直线l经过点B(2,4),
∴ 2-4+c=0,∴ c=2,即直线l的方程为x-y+2=0.
设C(x0,y0),由(1)知kAC=-1,即=-1.①
又∵ 线段AC的中点在直线l上,∴-+2=0.②
由①②得x0=-1,y0=3,∴ C(-1,3).
设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,
由题意可得解得
故△ABC外接圆的方程为x2+y2-x-y+5=0.
[2020·河南驻马店高一期末]已知△ABC三个顶点坐标为A(0,2),B(0,-2),C(-2,2).
(1)在△ABC中,求与BC边平行的中位线所在直线的方程;
(2)求△ABC外接圆的方程.
解:(1)由题意知,AC边的中点为(-1,2),AB边的中点为(0,0),
故与BC边平行的中位线所在直线方程为2x+y=0.
(2)设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0,
把A,B,C三点的坐标代入外接圆的方程,得
解得
故所求的圆的方程为x2+y2+2x-4=0.
过不共线的三点A,B,C的圆的方程的求法
1.待定系数法(代数法):设出圆的一般方程x2+y2+Dx+Ey+F=0,分别把三个点的坐标代入,求出待定系数D,E,F,即可求出圆的方程;
2.直接法(几何法):因为所求圆为△ABC的外接圆,所以△ABC任意两边的中垂线交点即为外接圆的圆心,顶点到圆心的距离即为外接圆的半径,代入圆的标准方程即可.
<4>点与圆的位置关系问题
例7 已知点A是圆C:x2+y2+ax+4y-5=0上任意一点,点A关于直线x+2y-1=0的对称点也在此圆上,则实数a= .
【解析】 由题意可知,圆C的圆心在直线x+2y-1=0上,则--4-1=0,解得a=-10.
【答案】 -10
[2020·浙江湖州高一检测]过点P(-3,0)作直线:2x+(λ+1)y+2λ=0(λ∈R)的垂线,垂足为M,已知点N(3,2),则当λ变化时,|MN|的取值范围是( )
A.[0,5+] B.[5- ,5+ ]
C.[5,5+ ] D.[5- ,5]
B
解析:直线2x+(λ+1)y+2λ=0(λ∈R),
即(2x+y)+λ(y+2)=0.
由得直线经过定点Q(1,-2).
由△PQM为直角三角形,斜边为PQ,M在以PQ为直径的圆上运动,
可得圆心为PQ的中点H(-1,-1),半径r=|PQ|=,
则|MN|的最大值为|NH|+r=+=5+;
|MN|的最小值为|NH|-r= -=5-.
故|MN|的取值范围为[5- ,5+ ].
题组三 与圆有关的轨迹问题
例8 已知点A(-2,0),B(2,0),动点P满足|PA|=λ|PB|(λ>0),若点P的轨迹为一条直线,则λ= ;若λ=2,则点P的轨迹方程为 .
【解题提示】 设P(x,y),把|PA|=λ|PB|两边平方,整理得,
(1-λ2)x2+(1-λ2)y2+4(1+λ2)x+4-4λ2=0,从而可得结果.
【解析】 设P(x,y),由|PA|=λ|PB|可得,=,
两边平方,整理得点P的轨迹方程为
(1-λ2)x2+(1-λ2)y2+4(1+λ2)x+4-4λ2=0.
若该方程表示直线,则解得λ=1.
当λ=2时,点P的轨迹方程为3x2+3y2-20x+12=0,
即x2+y2-x+4=0.
【答案】 1;x2+y2-x+4=0
已知圆C与y轴相切,圆心在直线x-2y=0上,且经过点A(2,3),求圆C的方程.
解:∵ 圆心在直线x-2y=0上,∴ 设圆心坐标为(2a,a).
又圆C与y轴相切,∴ 半径r=2|a|.
设圆C的标准方程为(x-2a)2+(y-a)2=4a2,
∵ 圆C经过点A(2,3),∴ (2-2a)2+(3-a)2=4a2,∴ a=1或a=13,
∴ 圆C的方程为(x-2)2+(y-1)2=4或(x-26)2+(y-13)2=676.
求轨迹方程的常用方法
1.直接法:直接利用条件建立x,y之间的关系F(x,y)=0.
2.定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义写出动点的轨迹方程.
3.代入(相关点)法:动点P(x,y)随另一动点Q(x0,y0)的变化而变化,常利用代入法求动点P(x,y)的轨迹方程.
小结
1.圆的标准方程
圆的标准方程:(x-a)2+(y-b)2=r2.
表示以点(a,b)为圆心,r为半径的圆.
2.点与圆的位置关系
点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
点M在圆外(x0-a)2+(y0-b)2>r2;
点M在圆上(x0-a)2+(y0-b)2=r2;
点M在圆内(x0-a)2+(y0-b)2
一般地,形式x2+y2+Dx+Ey+F=0,其中D,E,F都是常数.称为圆的一般方程.
(1)当 >0时,方程是以为圆心,为半径的圆的方程;
(2)当D2+E2-4F=0时,满足方程的实数只有x=-,y=-,所以原方程不是
圆的方程;
(3)当D2+E2-4F<0时,方程没有实数解,因而原方程也不是圆的方程.
