人教A版(2019)选择性必修第一册2.4.2 圆的一般方程 课件(共18张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册2.4.2 圆的一般方程 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 307.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 09:50:02 | ||
图片预览





文档简介
(共18张PPT)
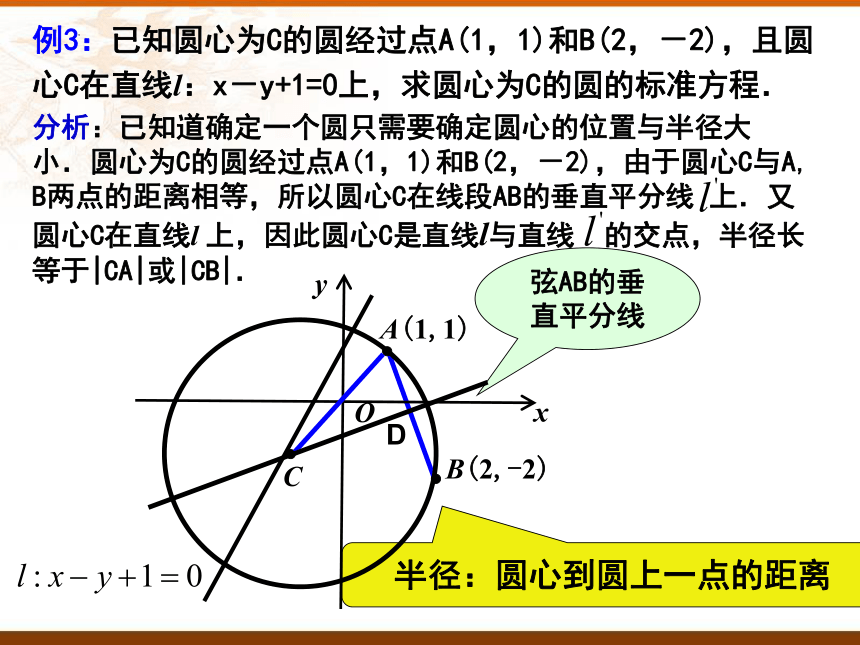
1.圆的标准方程:
表示圆心为A(a,b),半径为r的圆。
上节课知识要点
*注:特别的,圆心在坐标原点,半径长为r 的圆的方程是
2.点与圆的位置关系
A
x
y
o
M2
M3
M1
如果设点M到圆心的距离为d,则 点在圆外 d>r ; 点在圆上 d=r ;
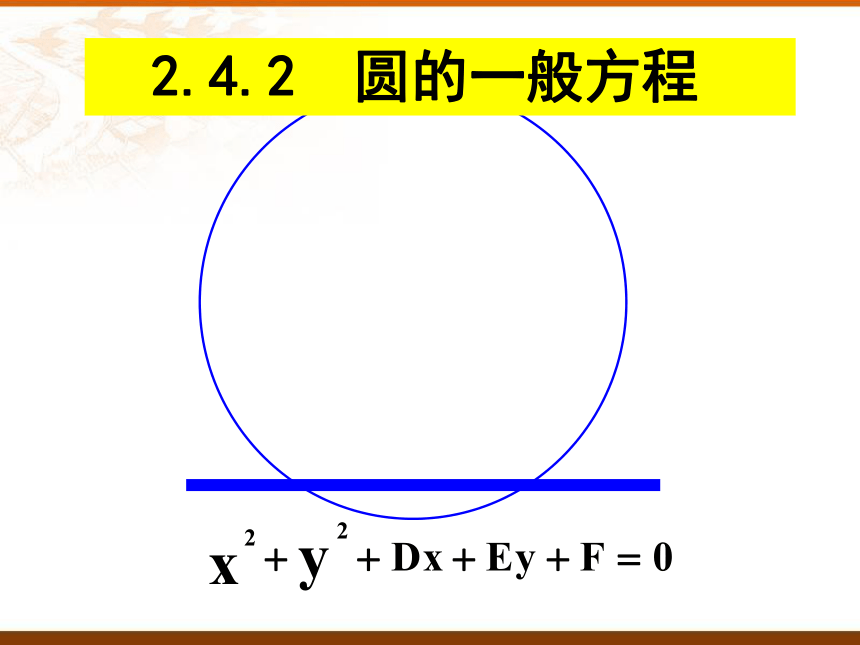
点在圆内 d例3:已知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
分析:已知道确定一个圆只需要确定圆心的位置与半径大小.圆心为C的圆经过点A(1,1)和B(2,-2),由于圆心C与A, B两点的距离相等,所以圆心C在线段AB的垂直平分线 上.又圆心C在直线l 上,因此圆心C是直线l与直线 的交点,半径长等于|CA|或|CB|.
半径:圆心到圆上一点的距离
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
D
解:因为A(1,1)和B(2,-2),所以线段AB中点D坐标为
直线AB的斜率:
因此线段AB的垂直平分线 的方程是
即
解方程组
得
所以圆心C的坐标是
圆心为C的圆的半径长
所以,圆心为C的圆的标准方程是
例3: 已知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
2.4.2 圆的一般方程
x2 +y2+Dx+Ey+F=0
把圆的标准方程(x-a)2+(y-b)2=r2
展开,得
-
2
2
2
2
2
2
0
2
=
-
+
+
-
+
r
b
a
by
ax
y
x
由于a,b,r均为常数
*结论:任何一个圆的方程都可以写成下面形式:
则 x2 +y2+Dx+Ey+F=0
引入新课
圆的一般方程
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
结论1:任何一个圆的方程都可以写成下面形式:
x2 +y 2+Dx+Ey+F=0
问:是不是任何一个形如
x2 +y 2+Dx+Ey+F=0的方程表
示的曲线都是圆呢?
请举例
配方,得
不一定表示圆
此方程表示以(1,-2)为圆心,半径为2的圆
配方,得
不是圆
结论2:
圆的一般方程
配方可得:
(3)当D2+E2-4F<0时,方程无实数解,所以
不表示任何图形。
把方程:x2+y2+Dx+Ey+F=0
(1)当D2+E2-4F>0 时,表示以( )为圆心, 以 为半径的圆
(2)当D2+E2-4F=0时,方程只有一组解 x=-D/2
y=-E/2,表示一个点( )
结论3:当D2+E2-4F>0时,形如x2+y2+Dx+Ey+F=0的二元二次方程表示一个圆
x2 +y2+Dx+Ey+F=0
圆的一般方程与标准方程的关系:
(D2+E2-4F>0)
(1)a=-D/2,b=-E/2,r =
没有xy这样的二次项
(2)标准方程易于看出圆心与半径
一般方程突出形式上的特点:
x2与y2系数相同并且不等于0;
D2+E2-4F>0
圆的一般方程
练习:判断下列方程能否表示圆的方程,若能的话写出圆心与半径
(1)x2+y2-2x+4y-4=0
(2)2x2+2y2-12x+4y=0
(3)x2+2y2-6x+4y-1=0
(4)x2+y2-12x+6y+50=0
(5)x2+y2-3xy+5x+2y=0
是
圆心(1,-2)半径3
是
圆心(3,-1),半径
不是
不是
不是
没有xy这样的二次项
圆的一般方程的特点:
x2与y2系数相同并且不等于0;
x2 +y2+Dx+Ey+F=0
D2+E2-4F>0
1.求下列各圆的圆心坐标和半径长.
解:
(1)圆心(3,0),半径3.
(2)圆心(0,-b),半径|b|.
请看课本P88:练习1
(1)表示点(0,0)
以(1,-2)为圆心,以 为半径的圆
(2)
(3)
表示以(-a,0)为圆心,以 为半径的圆
表示点(0,0)
请看课本P88:练习2
例题分析
例4:求过三点O(0,0),M1(1,1),M2(4,2)
的圆的方程,并求这个圆的半径长和圆心坐标.
解法2:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,-8)都在圆上,所以
所求圆的方程为
待定系数法2
例2: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
归纳:用“待定系数法”求圆的方程的一般步骤:
1、根据题意,选择标准方程(与圆心、半径有明显关系)或一般方程。
2、根据条件列出关于a、b、r 或D、E、F的方程组。
3、解出 a、b、r 或 D、E、F ,代入标准方程或一般方程。
例5、如下图,已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
x
o
y
B (4,3)
M(x,y)
A(x0,y0)
例题分析
解:设点M(x,y),A(x0 ,y0)
已知 B(4,3),且M是A、B的中点
x
y
o
A
B
M
例5:已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
①
②
把①代入②,得
1.圆的标准方程:
表示圆心为A(a,b),半径为r的圆。
上节课知识要点
*注:特别的,圆心在坐标原点,半径长为r 的圆的方程是
2.点与圆的位置关系
A
x
y
o
M2
M3
M1
如果设点M到圆心的距离为d,则 点在圆外 d>r ; 点在圆上 d=r ;
点在圆内 d
分析:已知道确定一个圆只需要确定圆心的位置与半径大小.圆心为C的圆经过点A(1,1)和B(2,-2),由于圆心C与A, B两点的距离相等,所以圆心C在线段AB的垂直平分线 上.又圆心C在直线l 上,因此圆心C是直线l与直线 的交点,半径长等于|CA|或|CB|.
半径:圆心到圆上一点的距离
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
D
解:因为A(1,1)和B(2,-2),所以线段AB中点D坐标为
直线AB的斜率:
因此线段AB的垂直平分线 的方程是
即
解方程组
得
所以圆心C的坐标是
圆心为C的圆的半径长
所以,圆心为C的圆的标准方程是
例3: 已知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
2.4.2 圆的一般方程
x2 +y2+Dx+Ey+F=0
把圆的标准方程(x-a)2+(y-b)2=r2
展开,得
-
2
2
2
2
2
2
0
2
=
-
+
+
-
+
r
b
a
by
ax
y
x
由于a,b,r均为常数
*结论:任何一个圆的方程都可以写成下面形式:
则 x2 +y2+Dx+Ey+F=0
引入新课
圆的一般方程
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
结论1:任何一个圆的方程都可以写成下面形式:
x2 +y 2+Dx+Ey+F=0
问:是不是任何一个形如
x2 +y 2+Dx+Ey+F=0的方程表
示的曲线都是圆呢?
请举例
配方,得
不一定表示圆
此方程表示以(1,-2)为圆心,半径为2的圆
配方,得
不是圆
结论2:
圆的一般方程
配方可得:
(3)当D2+E2-4F<0时,方程无实数解,所以
不表示任何图形。
把方程:x2+y2+Dx+Ey+F=0
(1)当D2+E2-4F>0 时,表示以( )为圆心, 以 为半径的圆
(2)当D2+E2-4F=0时,方程只有一组解 x=-D/2
y=-E/2,表示一个点( )
结论3:当D2+E2-4F>0时,形如x2+y2+Dx+Ey+F=0的二元二次方程表示一个圆
x2 +y2+Dx+Ey+F=0
圆的一般方程与标准方程的关系:
(D2+E2-4F>0)
(1)a=-D/2,b=-E/2,r =
没有xy这样的二次项
(2)标准方程易于看出圆心与半径
一般方程突出形式上的特点:
x2与y2系数相同并且不等于0;
D2+E2-4F>0
圆的一般方程
练习:判断下列方程能否表示圆的方程,若能的话写出圆心与半径
(1)x2+y2-2x+4y-4=0
(2)2x2+2y2-12x+4y=0
(3)x2+2y2-6x+4y-1=0
(4)x2+y2-12x+6y+50=0
(5)x2+y2-3xy+5x+2y=0
是
圆心(1,-2)半径3
是
圆心(3,-1),半径
不是
不是
不是
没有xy这样的二次项
圆的一般方程的特点:
x2与y2系数相同并且不等于0;
x2 +y2+Dx+Ey+F=0
D2+E2-4F>0
1.求下列各圆的圆心坐标和半径长.
解:
(1)圆心(3,0),半径3.
(2)圆心(0,-b),半径|b|.
请看课本P88:练习1
(1)表示点(0,0)
以(1,-2)为圆心,以 为半径的圆
(2)
(3)
表示以(-a,0)为圆心,以 为半径的圆
表示点(0,0)
请看课本P88:练习2
例题分析
例4:求过三点O(0,0),M1(1,1),M2(4,2)
的圆的方程,并求这个圆的半径长和圆心坐标.
解法2:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,-8)都在圆上,所以
所求圆的方程为
待定系数法2
例2: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
归纳:用“待定系数法”求圆的方程的一般步骤:
1、根据题意,选择标准方程(与圆心、半径有明显关系)或一般方程。
2、根据条件列出关于a、b、r 或D、E、F的方程组。
3、解出 a、b、r 或 D、E、F ,代入标准方程或一般方程。
例5、如下图,已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
x
o
y
B (4,3)
M(x,y)
A(x0,y0)
例题分析
解:设点M(x,y),A(x0 ,y0)
已知 B(4,3),且M是A、B的中点
x
y
o
A
B
M
例5:已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
①
②
把①代入②,得
