苏科版物理九年级上册课课练:专题训练:功、功率和机械效率的综合计算(含答案)
文档属性
| 名称 | 苏科版物理九年级上册课课练:专题训练:功、功率和机械效率的综合计算(含答案) | 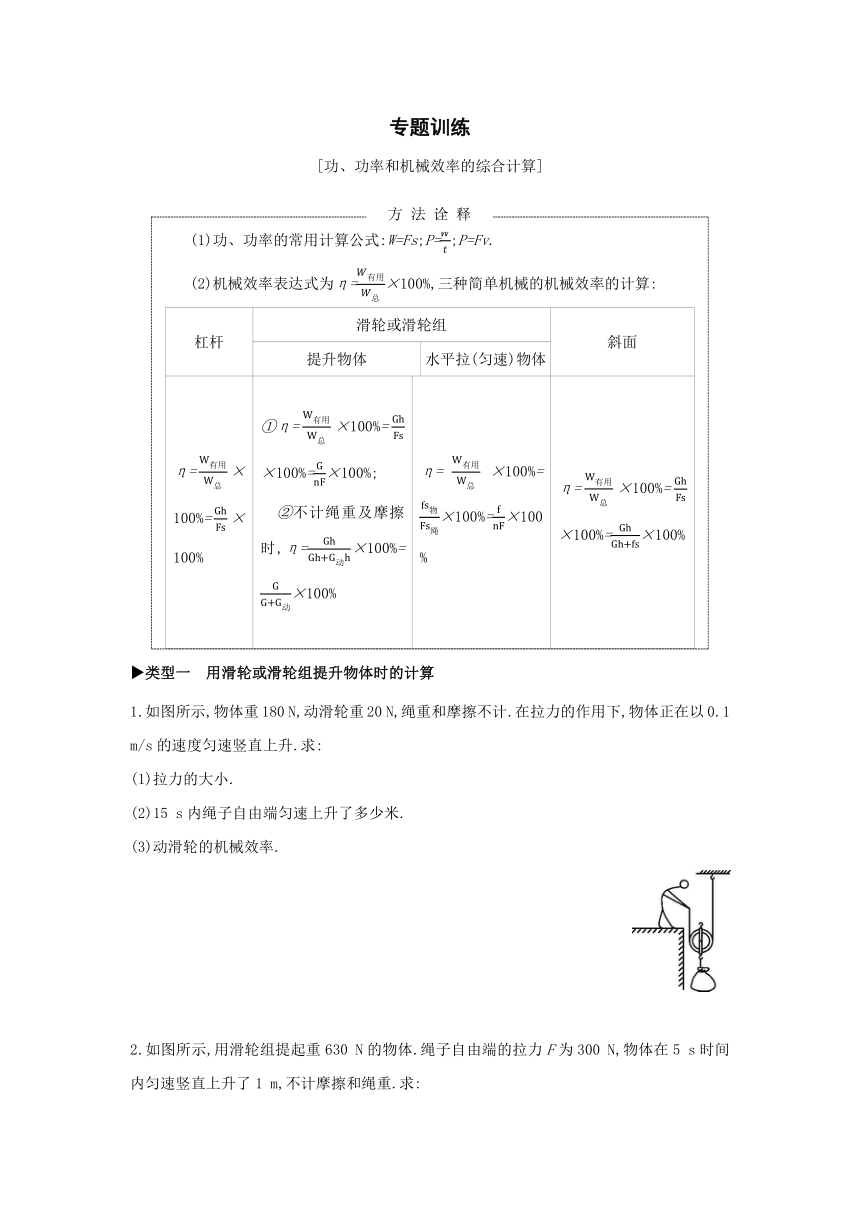 | |
| 格式 | docx | ||
| 文件大小 | 130.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-24 13:04:48 | ||
图片预览



文档简介
专题训练
[功、功率和机械效率的综合计算]
(
方 法 诠 释
)
(1)功、功率的常用计算公式:W=Fs;P=;P=Fv. (2)机械效率表达式为η=×100%,三种简单机械的机械效率的计算: 杠杆滑轮或滑轮组斜面提升物体水平拉(匀速)物体 η=×100%=×100% ①η=×100%=×100%=×100%; ②不计绳重及摩擦时,η=×100%=×100% η=×100%=×100%=×100% η=×100%=×100%=×100%
类型一 用滑轮或滑轮组提升物体时的计算
1.如图所示,物体重180 N,动滑轮重20 N,绳重和摩擦不计.在拉力的作用下,物体正在以0.1 m/s的速度匀速竖直上升.求:
(1)拉力的大小.
(2)15 s内绳子自由端匀速上升了多少米.
(3)动滑轮的机械效率.
2.如图所示,用滑轮组提起重630 N的物体.绳子自由端的拉力F为300 N,物体在5 s时间内匀速竖直上升了1 m,不计摩擦和绳重.求:
(1)滑轮组对物体所做的有用功.
(2)拉力做功的功率.
(3)滑轮组的机械效率.
(4)若在不超过绳子能承受的最大拉力的情况下,用此滑轮组提起重为730 N的物体时,此滑轮组的机械效率。
3.如图所示为一种塔式起重机上的滑轮组.现用该滑轮组将重为1.8×104 N的钢材以0.6 m/s的速度竖直向上匀速起吊,已知所用拉力为8×103 N,钢材被吊起10 m的高度,克服绳重和摩擦做的功是有用功的10%.求:
(1)提升钢材所做的有用功.
(2)起重机的机械效率.
(3)克服动滑轮重做功的功率.
类型二 用斜面提升物体时的计算
4.[2019·乐山] 如图所示,在斜面上将一个重600 N的物体匀速拉到高处,沿斜面向上的拉力F=400 N,拉动的距离s=4.5 m,提升高度h=1.8 m,所用时间t=30 s.拉力F做功的功率为 W,此过程中物体受到的摩擦力为 N.
5.如图所示,工人用沿斜面向上且大小为500 N的推力,将重800 N的货物从A点匀速推至B点;再用100 N的水平推力使其沿水平台面匀速直线运动5 s,到达C点.已知AB长3 m,BC长1.2 m,距地面高1.5 m.试问:
(1)利用斜面搬运货物主要是为了 .
(2)货物在水平台面上运动的速度为多少
(3)水平推力做功的功率为多少
(4)斜面的机械效率为多少
6.在斜面上将一个质量为0.4 kg的物体,从底端沿斜面匀速拉到顶端(如图所示),所用时间为4 s,斜面长s=1 m、高h=0.2 m,该斜面的机械效率为80%.求:(g取10 N/kg)
(1)物体受到的重力.
(2)拉力所做的有用功.
(3)拉力所做的总功和拉力做功的功率.
(4)物体在斜面上受到的摩擦力.
类型三 用杠杆提升物体时的计算
7.如图所示,用一根均匀的细木棒OC提升物体,OA=OC,B为OC的中点.在C点用始终竖直向上的50 N的拉力将挂在A点重为180 N的物体匀速提升0.1 m.提升该物体做的有用功是 J,总功是 J,木棒的机械效率为 ,木棒重为 N.(不计摩擦)
8.[2019·泰州] 如图所示,使用杠杆提升重物,拉力F竖直向下,重物匀速缓慢上升,相关数据如图下表,求:
物重G/N 拉力F/N 时间t/s A端上升的竖直距离h/m B端下降的竖直距离s/m
200 500 0.5 0.4 0.2
(1)拉力所做的功.
(2)拉力做功的功率.
(3)此过程中,该杠杆的机械效率.
9.小金用如图所示的实验装置测量杠杆的机械效率.实验时竖直向上匀速拉动杠杆,使挂在杠杆下面的钩码缓缓上升.问:(支点和杠杆的摩擦不计)
(1)重为5 N的钩码挂在A点时,人的拉力F为4 N,钩码上升0.3 m时,动力作用点C上升0.5 m,此时杠杆的机械效率η1为多大
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5 m.则:人的拉力F与第一次相比 (选填“变大”“变小”或“不变”).比较此时杠杆的机械效率η2与η1的大小并用学过的知识给予推导.
答案
专题训练(二)
[功、功率和机械效率的综合计算]
1.(1)不计绳重和摩擦,拉力F=(G+G动)=×(180 N+20 N)=100 N.
(2)绳子移动的速度:
v绳=2v物=2×0.1 m/s=0.2 m/s,
15 s内绳子自由端匀速上升的距离:
s=v绳t=0.2 m/s×15 s=3 m.
(3)动滑轮的机械效率:
η=×100%=×100%=×100%=×100%=90%.
2.(1)滑轮组对物体所做的有用功:
W有用=Gh=630 N×1 m=630 J.
(2)n=3,绳子自由端移动的距离:s=3h=3×1 m=3 m,
拉力做的功:W总=Fs=300 N×3 m=900 J,
拉力做功的功率:P===180 W.
(3)滑轮组的机械效率:η=×100%=×100%=70%.
(4)W额外=W总-W有用=900 J-630 J=270 J,
不计摩擦和绳重,G动===270 N,
η=×100%=×100%=×100%,
所以,用此滑轮组提起重为730 N的物体时,此滑轮组的机械效率:
η'=×100%=×100%=73%.
3.(1)提升钢材所做的有用功:W有用=Gh=1.8×104 N×10 m=1.8×105 J.
(2)由图知n=3,则拉力端移动的距离:
s=3h=3×10 m=30 m,
拉力做的总功:W总=Fs=8×103 N×30 m=2.4×105 J,
起重机的机械效率:η=×100%=×100%=75%.
(3)克服绳重和摩擦做的功是有用功的10%,则克服动滑轮重做的功:
W额动=W总-W有用-10%W有用=2.4×105 J-1.8×105 J-10%×1.8×105 J=4.2×104 J,
所用时间:t=== s,
克服动滑轮重做功的功率:P===2520 W.
4.60 160
(1)拉力所做的总功:
W总=Fs=400 N×4.5 m=1800 J,
拉力F做功的功率:P===60 W.
(2)有用功:W有用=Gh=600 N×1.8 m=1080 J,
克服摩擦力做的额外功:W额外=W总-W有用=1800 J-1080 J=720 J,
由W额外=fs得,物体所受斜面的摩擦力:f===160 N.
5.(1)省力
(2)货物在水平台面上运动的速度:v===0.24 m/s.
(3)水平推力做功的功率:P=Fv=100 N×0.24 m/s=24 W.
(4)在斜面上推力做的功:W总=F's'=500 N×3 m=1500 J;
做的有用功:W有用=Gh=800 N×1.5 m=1200 J;
则斜面的机械效率:η=×100%=×100%=80%.
6.(1)物体受到的重力:G=mg=0.4 kg×10 N/kg=4 N.
(2)拉力所做的有用功:W有用=Gh=4 N×0.2 m=0.8 J.
(3)由η=×100%可得,拉力做的总功:W总===1 J,
拉力做功的功率:P===0.25 W.
(4)因为W总=W有用+W额外,所以额外功:W额外=W总-W有用=1 J-0.8 J=0.2 J,
由W额外=fs得,摩擦力:f===0.2 N.
7.18 20 90% 10
(1)提升该物体做的有用功:W有用=Gh=180 N×0.1 m=18 J.
(2)因为OA=OC,所以拉力端移动的距离:s=4h=4×0.1 m=0.4 m;
提升该物体做的总功:W总=Fs=50 N×0.4 m=20 J;
木棒的机械效率:η=×100%=×100%=90%.
(3)W总=W有用+W额外,不计摩擦,克服木棒重力做的功是额外功,
W额外=W总-W有用=20 J-18 J=2 J,
因为OA=OC,B为OC的中点,所以OB=2OA;由相似三角形的知识可知,当物体上升0.1 m时,B点(重心)将上升h'=0.2 m,
不计摩擦,由W额外=G木h'可得木棒的重力:G木===10 N.
8.(1)拉力所做的功:W总=Fs=500 N×0.2 m=100 J.
(2)拉力做功的功率:P===200 W.
(3)此过程中,有用功:W有用=Gh=200 N×0.4 m=80 J,
杠杆的机械效率:η=×100%=×100%=80%.
9.(1)有用功:W有用=Gh=5 N×0.3 m=1.5 J,总功:W总=Fs=4 N×0.5 m=2 J,
杠杆的机械效率:η1=×100%=×100%=75%.
(2)变小 杠杆的机械效率:η=×100%=×100%=×100%.因为杠杆上升的高度不变,所以克服杠杆自重所做的额外功不变,由于悬挂点B更接近支点,所以钩码被提升的高度减小,根据W有用=Gh可知,有用功减小;从上面η的表达式可知,W有用减小、W额外不变,所以变大,分母变大,η减小,即η2<η1.
[功、功率和机械效率的综合计算]
(
方 法 诠 释
)
(1)功、功率的常用计算公式:W=Fs;P=;P=Fv. (2)机械效率表达式为η=×100%,三种简单机械的机械效率的计算: 杠杆滑轮或滑轮组斜面提升物体水平拉(匀速)物体 η=×100%=×100% ①η=×100%=×100%=×100%; ②不计绳重及摩擦时,η=×100%=×100% η=×100%=×100%=×100% η=×100%=×100%=×100%
类型一 用滑轮或滑轮组提升物体时的计算
1.如图所示,物体重180 N,动滑轮重20 N,绳重和摩擦不计.在拉力的作用下,物体正在以0.1 m/s的速度匀速竖直上升.求:
(1)拉力的大小.
(2)15 s内绳子自由端匀速上升了多少米.
(3)动滑轮的机械效率.
2.如图所示,用滑轮组提起重630 N的物体.绳子自由端的拉力F为300 N,物体在5 s时间内匀速竖直上升了1 m,不计摩擦和绳重.求:
(1)滑轮组对物体所做的有用功.
(2)拉力做功的功率.
(3)滑轮组的机械效率.
(4)若在不超过绳子能承受的最大拉力的情况下,用此滑轮组提起重为730 N的物体时,此滑轮组的机械效率。
3.如图所示为一种塔式起重机上的滑轮组.现用该滑轮组将重为1.8×104 N的钢材以0.6 m/s的速度竖直向上匀速起吊,已知所用拉力为8×103 N,钢材被吊起10 m的高度,克服绳重和摩擦做的功是有用功的10%.求:
(1)提升钢材所做的有用功.
(2)起重机的机械效率.
(3)克服动滑轮重做功的功率.
类型二 用斜面提升物体时的计算
4.[2019·乐山] 如图所示,在斜面上将一个重600 N的物体匀速拉到高处,沿斜面向上的拉力F=400 N,拉动的距离s=4.5 m,提升高度h=1.8 m,所用时间t=30 s.拉力F做功的功率为 W,此过程中物体受到的摩擦力为 N.
5.如图所示,工人用沿斜面向上且大小为500 N的推力,将重800 N的货物从A点匀速推至B点;再用100 N的水平推力使其沿水平台面匀速直线运动5 s,到达C点.已知AB长3 m,BC长1.2 m,距地面高1.5 m.试问:
(1)利用斜面搬运货物主要是为了 .
(2)货物在水平台面上运动的速度为多少
(3)水平推力做功的功率为多少
(4)斜面的机械效率为多少
6.在斜面上将一个质量为0.4 kg的物体,从底端沿斜面匀速拉到顶端(如图所示),所用时间为4 s,斜面长s=1 m、高h=0.2 m,该斜面的机械效率为80%.求:(g取10 N/kg)
(1)物体受到的重力.
(2)拉力所做的有用功.
(3)拉力所做的总功和拉力做功的功率.
(4)物体在斜面上受到的摩擦力.
类型三 用杠杆提升物体时的计算
7.如图所示,用一根均匀的细木棒OC提升物体,OA=OC,B为OC的中点.在C点用始终竖直向上的50 N的拉力将挂在A点重为180 N的物体匀速提升0.1 m.提升该物体做的有用功是 J,总功是 J,木棒的机械效率为 ,木棒重为 N.(不计摩擦)
8.[2019·泰州] 如图所示,使用杠杆提升重物,拉力F竖直向下,重物匀速缓慢上升,相关数据如图下表,求:
物重G/N 拉力F/N 时间t/s A端上升的竖直距离h/m B端下降的竖直距离s/m
200 500 0.5 0.4 0.2
(1)拉力所做的功.
(2)拉力做功的功率.
(3)此过程中,该杠杆的机械效率.
9.小金用如图所示的实验装置测量杠杆的机械效率.实验时竖直向上匀速拉动杠杆,使挂在杠杆下面的钩码缓缓上升.问:(支点和杠杆的摩擦不计)
(1)重为5 N的钩码挂在A点时,人的拉力F为4 N,钩码上升0.3 m时,动力作用点C上升0.5 m,此时杠杆的机械效率η1为多大
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5 m.则:人的拉力F与第一次相比 (选填“变大”“变小”或“不变”).比较此时杠杆的机械效率η2与η1的大小并用学过的知识给予推导.
答案
专题训练(二)
[功、功率和机械效率的综合计算]
1.(1)不计绳重和摩擦,拉力F=(G+G动)=×(180 N+20 N)=100 N.
(2)绳子移动的速度:
v绳=2v物=2×0.1 m/s=0.2 m/s,
15 s内绳子自由端匀速上升的距离:
s=v绳t=0.2 m/s×15 s=3 m.
(3)动滑轮的机械效率:
η=×100%=×100%=×100%=×100%=90%.
2.(1)滑轮组对物体所做的有用功:
W有用=Gh=630 N×1 m=630 J.
(2)n=3,绳子自由端移动的距离:s=3h=3×1 m=3 m,
拉力做的功:W总=Fs=300 N×3 m=900 J,
拉力做功的功率:P===180 W.
(3)滑轮组的机械效率:η=×100%=×100%=70%.
(4)W额外=W总-W有用=900 J-630 J=270 J,
不计摩擦和绳重,G动===270 N,
η=×100%=×100%=×100%,
所以,用此滑轮组提起重为730 N的物体时,此滑轮组的机械效率:
η'=×100%=×100%=73%.
3.(1)提升钢材所做的有用功:W有用=Gh=1.8×104 N×10 m=1.8×105 J.
(2)由图知n=3,则拉力端移动的距离:
s=3h=3×10 m=30 m,
拉力做的总功:W总=Fs=8×103 N×30 m=2.4×105 J,
起重机的机械效率:η=×100%=×100%=75%.
(3)克服绳重和摩擦做的功是有用功的10%,则克服动滑轮重做的功:
W额动=W总-W有用-10%W有用=2.4×105 J-1.8×105 J-10%×1.8×105 J=4.2×104 J,
所用时间:t=== s,
克服动滑轮重做功的功率:P===2520 W.
4.60 160
(1)拉力所做的总功:
W总=Fs=400 N×4.5 m=1800 J,
拉力F做功的功率:P===60 W.
(2)有用功:W有用=Gh=600 N×1.8 m=1080 J,
克服摩擦力做的额外功:W额外=W总-W有用=1800 J-1080 J=720 J,
由W额外=fs得,物体所受斜面的摩擦力:f===160 N.
5.(1)省力
(2)货物在水平台面上运动的速度:v===0.24 m/s.
(3)水平推力做功的功率:P=Fv=100 N×0.24 m/s=24 W.
(4)在斜面上推力做的功:W总=F's'=500 N×3 m=1500 J;
做的有用功:W有用=Gh=800 N×1.5 m=1200 J;
则斜面的机械效率:η=×100%=×100%=80%.
6.(1)物体受到的重力:G=mg=0.4 kg×10 N/kg=4 N.
(2)拉力所做的有用功:W有用=Gh=4 N×0.2 m=0.8 J.
(3)由η=×100%可得,拉力做的总功:W总===1 J,
拉力做功的功率:P===0.25 W.
(4)因为W总=W有用+W额外,所以额外功:W额外=W总-W有用=1 J-0.8 J=0.2 J,
由W额外=fs得,摩擦力:f===0.2 N.
7.18 20 90% 10
(1)提升该物体做的有用功:W有用=Gh=180 N×0.1 m=18 J.
(2)因为OA=OC,所以拉力端移动的距离:s=4h=4×0.1 m=0.4 m;
提升该物体做的总功:W总=Fs=50 N×0.4 m=20 J;
木棒的机械效率:η=×100%=×100%=90%.
(3)W总=W有用+W额外,不计摩擦,克服木棒重力做的功是额外功,
W额外=W总-W有用=20 J-18 J=2 J,
因为OA=OC,B为OC的中点,所以OB=2OA;由相似三角形的知识可知,当物体上升0.1 m时,B点(重心)将上升h'=0.2 m,
不计摩擦,由W额外=G木h'可得木棒的重力:G木===10 N.
8.(1)拉力所做的功:W总=Fs=500 N×0.2 m=100 J.
(2)拉力做功的功率:P===200 W.
(3)此过程中,有用功:W有用=Gh=200 N×0.4 m=80 J,
杠杆的机械效率:η=×100%=×100%=80%.
9.(1)有用功:W有用=Gh=5 N×0.3 m=1.5 J,总功:W总=Fs=4 N×0.5 m=2 J,
杠杆的机械效率:η1=×100%=×100%=75%.
(2)变小 杠杆的机械效率:η=×100%=×100%=×100%.因为杠杆上升的高度不变,所以克服杠杆自重所做的额外功不变,由于悬挂点B更接近支点,所以钩码被提升的高度减小,根据W有用=Gh可知,有用功减小;从上面η的表达式可知,W有用减小、W额外不变,所以变大,分母变大,η减小,即η2<η1.
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
